A 100 legnagyobb hazugság a fizikában

 Írta: Ray Fleming

2017

TARTALOM

Bajban van a fizika

1. hazugság: Nincs éter

2. hazugság: Michelson és Morley megcáfolta az étert

3. hazugság: Hullám-részecske kettősség

4. hazugság: A fotonok elemiek

5. hazugság: Virtuális fotonok

6. hazugság: Az éter virtuális foton

7. hazugság: A fotonok erőhordozók

8. hazugság: Az elektromágneses mezők nem valósak

9. hazugság: Az elektromágneses elmélet megmagyarázza a mozgást

10. hazugság: Mágneses monopólusok

11. hazugság: A fénysebesség minden referenciakeretben állandó

12. hazugság: A fénysebesség minden megfigyelő számára állandó

13. hazugság: Speciális relativitáselmélet

14. hazugság: Hossz-összehúzódás

15. hazugság: Térösszehúzódás

16. hazugság: A tér időtágulása

17. hazugság: Hatás távolról

18. hazugság: Mérőbozonok

19. hazugság: A tömeg mint belső tulajdonság

20. hazugság: tömegpont

21. hazugság: Az anyag és az antianyag belső tulajdonság

22. hazugság: A tehetetlenség belső tulajdonság

23. hazugság: Nincs mechanikus erő

24. hazugság: A fizika megmagyarázza a mechanikai mozgást

25. hazugság: A sötét energia nem erő

26. hazugság: A gravitáció alapvető erő

27. hazugság: A sötét energia nem okoz tágulást

28. hazugság: A nem-tér létezése

29. hazugság: Az ősrobbanás figyelmen kívül hagyhatja a sötét energiát

30. hazugság: Az ősrobbanás meghaladhatja a fénysebességet

31. hazugság: Az inflációs hipotézis

32. hazugság: A kozmikus mikrohullámú háttér az ősrobbanást bizonyítja

33. hazugság: Az ősrobbanás megsértheti az energia-megmaradást

34. hazugság: Az ősrobbanás

35. hazugság: Ciklikus univerzum

36. hazugság: A gravitáció sebessége a fény sebessége

37. hazugság: Az elektromágneses mezők sebessége végtelen

38. hazugság: Az elektromágneses mezők fénysebességgel terjednek

39. hazugság: A horizont probléma

40. hazugság: Az általános relativitáselmélet megmagyarázza a gravitációs gyorsulást

41. hazugság: A Van der Waals erők nem magyarázzák a gravitációt

42. hazugság: Az általános relativitáselmélet figyelmen kívül hagyhatja a vákuum energiát

43. hazugság: Görbült tér

44. hazugság: Általános relativitáselmélet

45. hazugság: Gravitációs időtágulás

46. ​​hazugság: A gravitációs időtágulás az általános relativitáselmélet bizonyítéka

47. hazugság: Az ekvivalencia elve bizonyítja az általános relativitáselméletet

48. hazugság: Sötét anyag

49. hazugság: Gravitonok

50. hazugság: A gravitáció az energia minden formájának köszönhető

51. hazugság: A gravitáció a tömegnek köszönhető

52. hazugság: A Pauli-féle kizárási elv

53. hazugság: A töltés belső tulajdonság

54. hazugság: Pontszerű részecskék

55. hazugság: Kis elektronok

56. hazugság: Az elektronok és a protonok között nincs taszító erő

57. hazugság: A Schrödinger-egyenlet az elektronok mozgását írja le

58. hazugság: A fizika megmagyarázza a foton-kibocsátást

59. hazugság: A semleges pion kvark modell

60. hazugság: A többi irracionális Mezon-modell

61. hazugság: A kvarkok

62. hazugság: A müonok elemi részecskék

63. hazugság: A tauonok elemi részecskék

64. hazugság: Az elektron-neutrínók elemiek

65. hazugság: A Mü és Tau neutrínók elemiek

66. hazugság: A neutrínóknak tömegük van

67. hazugság: A W & Z bozonok gyenge kölcsönhatást közvetítenek

68. hazugság: W & Z részecskék

69. hazugság: Az erős nukleáris kölcsönhatás a gluonoknak köszönhető

70. hazugság: Gluonok

71. hazugság: Az elektronokra nem hat az erős kölcsönhatás

72. hazugság: Leptonok

73. hazugság: A protonok nem elemi részecskék

74. hazugság: A neutronok nem elektronok és nem protonok

75. hazugság: A részecskéknek relativisztikus tömegük van

76. hazugság: A tömeg a Higgs-mezőnek köszönhető

77. hazugság: A Higgs-bozon

78. hazugság: A bozonok elemi részecskék

79. hazugság: Az elemi részecskék táblázata

80. hazugság: A koppenhágai értelmezés

81. hazugság: Kísérteties akció távolról

82. hazugság: A sok-világ értelmezése

83. hazugság: A kvantummechanika hullámmodellje

84. hazugság: A Kaluza-Klein elmélet

85. hazugság: Húrelmélet

86. hazugság: Extra fizikai dimenziók

87. hazugság: A fénysebesség alapvető

88. hazugság: Gyorsabban, mint a fény

89. hazugság: Tachionok

90. hazugság: A fennmaradó hipotetikus részecskék

91. hazugság: G egy alapvető állandó

92. hazugság: A gravitációs képlet fordított négyzetes törvénye

93. hazugság: Degenerációs nyomás

94. hazugság: A neutroncsillag mérethatára

95. hazugság: Relativisztikus fekete lyukak

96. hazugság: Hawking-sugárzás

97. hazugság: Szingularitások

98. hazugság: Féreglyukak

99. hazugság: Az anyagtermelés sérti az energiamegmaradás elvét

100. hazugság: Négy alapvető erő létezik

És most?

Becstelen említések

Baj a fizikával

„Nagyon erősen érzem, hogy a fizika elért szakasza napjainkban nem a végső szakasz. Ez csak egy szakasza a természetről alkotott képünk fejlődésének, és számítanunk kell arra, hogy ez az evolúciós folyamat a jövőben is folytatódik, ahogy a biológiai is.

A fizikai elmélet jelenlegi szakasza csupán egy lépcsőfok a jövőbeni jobb szakaszok felé. Egészen biztosak lehetünk benne, hogy lesznek jobb szakaszok, pusztán a mai fizikában előforduló nehézségek miatt.” 1.

Paul Dirac, 1963

Ez a könyv nem a tudomány elleni háború része, hanem a tudomány tisztaságáért vívott harc. Mert a fizikusok olyan elméletek tömegében kezdtek el hinni, amelyek legnagyobb részt összeegyeztethetetlenek egymással, és ami még tragikusabb: ellentmondanak a fizikai bizonyítékoknak! Dirac álma egy egyszerűbb fizikáról így nem valósult meg. Ha valami, épp a fizika vált egyre bonyolultabbá.

A fizikusok eddig azt képzelték, hogy végül egyetlen erővel, néhány elemi részecskével és néhány alapvető állandóval le lehet írni az univerzumot, de senki sem akarja elvégezni azt a nehéz munkát, hogy eltávolítsuk a hamis fizika fölösleges ballasztjait annak érdekében, hogy megmaradjunk a lehetséges elméletek közül a legegyszerűbbnél.

Teljesen hiányzik a kritikai gondolkodás a fővonalas fizikából. Sehol sem nagyobbak ezek az ellentmondások, mint azoknál az elméleteknél, amelyek nem veszik figyelembe a vákuum energiáját, a nullpont energiát.

A 20. századi fizikai elméletek nagy részét a vákuumenergia figyelmen kívül hagyásával, vagy éppen a vákuumenergiát magában foglaló elméletek ellenében fejlesztették ki.

Ám a fizikusok túlnyomó többsége ma már felismeri, hogy a nullponti energia valóban létezik, de mégsem akarják átírni a nullponti energia létezését elutasító tudósok elméleteit.

Más fontos elméletek meg egyszerűen figyelmen kívül hagyják a fizika alapelveit, például az energia-megmaradás elvét vagy az anyagtestek mozgásának fénysebesség-határát.

A legnépszerűbb hipotézis, amely figyelmen kívül hagyja mindkét elvet, az ősrobbanás modell. De sok más elmélet is figyelmen kívül hagyja ezeket és más fontos fizikai elveket. Ez a józan fizika elveinek tetszés szerinti alkalmazását és a kritikai gondolkodás hiányát mutatja egyes fizikusok részéről, akik ezáltal visszás szakmai gyakorlatot folytatnak.

Másrészt a fizikusok olyan szabályokat találtak ki, amelyek úgy tűnt nekik, hogy leírják látottakat, és fiktív neveket adtak ezeknek az alapelveknek, amikor kiderült, hogy ezek nem megalapozottak az univerzumunk valódi fizikai valóságának a megértésében.

A részecskék nem „ismerik” a szabályokat, de „ismerik” a fizikai korlátaikat. Ezen kitalált szabályok némelyikét nagyobb tisztelettel kezelik, mint a valódi elveket, amik a fizikai tényeken alapszanak.

A fizikai elméletek hibái más természettudományokat is megfertőztek, mint például a kémiát, a csillagászatot, a geológiát és a biológiát. A fizika elvileg a legegyszerűbb az összes természettudomány közül, mára mégis rendkívül bonyolult lett.

Alapjai, az elemi részecskék és az alapvető erők, amiknek legalábbis a legegyszerűbbnek kell lenniük, de ahogy ezeket az alapokat egyre több tárgyra és kölcsönhatásra alkalmazzák, rendkívül bonyolulttá válnak.

A többi természettudomány még tovább fokozza ezt a bonyolultságot, így az alapvető fizikai elméletekkel kapcsolatos problémák megsokszorozódnak. A gravitációhoz hasonló alapvető erő megértésének hibája számos csillagászati elméletet tesz érvénytelenné. Szerencsére a megfigyelés továbbra is fontos a valódi tudomány számára, mivel a jól végzett kísérletek és megfigyelések eredményei felülírják a rossz elméleteket.

A gravitációt itt nem mellékesen hozzuk fel, mert ha figyelmen kívül hagyjuk a vákuumenergiát, akkor nincs elég tömeg ahhoz, hogy az általános relativitáselmélet modellje helyes legyen, de ha nem hagyjuk figyelmen kívül, akkor meg túl sok az energia ahhoz, hogy az állítása igaz legyen. Tehát ez az elmélet is egy alapvető kudarc a kritikai gondolkodás hiánya miatt, amely áthatja a jelenlegi fizika egész standard modelljét.

Másrészt a legalapvetőbb fizikán kívüli tudomány, a matematika folyamatosan harcban áll a fizikusok figyelméért, mivel a matematikusok és az elméleti fizikusok mindig olyan fizikai jelenséget keresnek, amely illeszkedik a kedvenc matematikai elméletükhöz. A matematikusok és az elméleti fizikusok azt akarják hinni, hogy mindenféle matematikai elmélet, amelyen dolgoznak, valami valós fizikailag jelenséghez kapcsolódik, de az igazság az, hogy a legtöbb egyáltalán nem kapcsolódnak semmihez. Ennek egyik leghíresebb példája a húrelmélet.

A másik probléma a fizikával foglalkozó matematikusokkal az, hogy úgy tesznek, mintha egy matematikai modell teljes fizikaelmélet lenne. De nem az. A fizika tudománya a matematikai modellek mellett fizikai magyarázatokat is igényel. Ha nem hiszed, nézd meg a fizika definícióját. Minden teljes fizikaelméletben léteznie kell fizikai leírásnak is a dolgok működéséről.

Minden kölcsönhatás mögött fizikai mechanizmusok állnak. Minden mozog, mert valahogyan nyomóerő hatása alatt van. Sok esetben ezek a fizikai mechanizmusok hiányoznak a népszerű elméletekből. A gravitáció ismét remek példa erre a problémára, mivel az általánosan elfogadott elméletek nem tartalmaznak fizikai modellt a testek nyomóerő alatti viselkedésére. A gyorsuláshoz erő kell, az erő pedig azt jelenti, hogy valami nyomja a testet. Ám ennek a valami erőnek és valahogyan működésének a kitalálása alapvető a tudomány számára, amit nem lehet egyszerűen figyelmen kívül hagyni.

Néhány probléma a standard modellel olyan kérdésekkel kezdődik, amelyeket már fel sem tesznek. Ez a helyzet a mechanika legalapvetőbb kérdésével is, hogy mi a tehetetlenség jelensége és hogy miként működik? A másik alapvető kérdés, hogy a foton miért rendelkezik forgó elektromos és mágneses mezővel? És ha az ember feltesz egyet is e határokat feszegető alapvető kérdések közül, azt kockáztatja, hogy őrültnek bélyegzik, különösen akkor, ha valamit meg is próbál tenni a kérdés megválaszolására. Bármely mechanikai elmélet hiányos a tehetetlenség mechanikájának ismerete nélkül.

A foton bármely elmélete hiányos a forgó elektromos és mágneses mezők keletkezési okának leírása nélkül. Egy másik híresen fel nem tett kérdés, hogy mi az az erő, amely megakadályozza, hogy egy elektron a protonba zuhanjon? Ha az egyedüli erő az elektrosztatika lenne, akkor a proton és az elektron a pozitív és negatív töltésük miatt gyorsan egyesülnének. Ha ez megtörténne, nem létezne hidrogén atom, sőt, semmilyen más atom vagy molekula sem. Akkor az összes szabad proton és elektron neutronokat képezne, és minden csillag neutroncsillag lenne.

A problémák széles csoportja is kapcsolódik annak meghatározásához, hogy mely dolgok elemiek és melyek nem. Képzeld, mi van, ha valami elemibb dolgokból mintázható, mint az, hogy valami nem elemi. Az ilyen típusú kérdések nagy része a részecskeelméletben találhatók. Mely részecskék elemi részecskék és melyek nem? Mely „részecskék” valójában más elemibb részecskék kombinációinak rezonáns állapotai?

Sajnos a Nobel-díjat nem adják ki azoknak, akik új rezonanciaállapotot fedeznek fel, ezért a fizikusok ragaszkodnak ahhoz, hogy minden új rezonanciaállapot, amelyet felfedeznek, egy részecske legyen, hogy megszerezzék a díjukat. Ennek a tevékenységnek az a következménye, hogy a részecskeelmélet egyre bonyolultabbá válik, nem pedig egyre egyszerűbbé, ahogy kellene. Tovább rontja a helyzetet, hogy a fizikusok szeretnek új részecskéket feltalálni, hogy megpróbálják megmagyarázni azokat a dolgokat, amelyeket nem értenek, ahelyett, hogy olyan dolgokkal magyaráznák meg őket, amelyekről ismert, hogy fizikailag léteznek.

Az „elemi vagy nem” problémák gyűjteménye egy tágabb problémacsoport egy részhalmaza, amely egy kísérleti eredmény helyes értelmezésének meghatározásához kapcsolódik, ha egynél több lehetséges magyarázat van. Ennek tipikus példája egy részecskeütközési kísérlet, ahol az egyik típusú részecskét egy másik típusú részecskére lőtték ki, és a kísérlet nem mutat szórást. Ez azt jelenti, hogy a célrészecske kicsi az energetikai részecskéhez képest, vagy azt jelenti, hogy a célrészecske nagyobb, mint a felgyorsított részecske, és átlátszó számára? Ha van más kísérleti bizonyíték arra vonatkozóan, hogy a célrészecske valóban nagy, egyszerűen figyelmen kívül hagyják a bizonyítékokat, így továbbra is azt hihetik, hogy kicsi.

Ez is egy példa a kritikai gondolkodás hiányosságaira, amelyek gyakoriak a fizikusok körében. Sok esetben egynél több magyarázata van egy kísérleti eredménynek, de a fizikusok továbbra is ragaszkodnak ahhoz, hogy a rossz értelmezés a helyes, még akkor is, ha tudományos bizonyítékok állnak rendelkezésre ennek ellenkezőjére.

A problémák következő osztálya akkor jön létre, amikor a fizikusok elfelejtik elvégezni a munkájukat, és egyszerűen belső neveznek egy tulajdonságot. Ez a belső tulajdonság egy dolognak a többitől független tulajdonsága. Ez elég ártatlanul hangzik, nem? A fizikusok számára azonban felelősségükről való lemondás, ha fizikailag nem magyarázzák el, hogy mi történik valójában.

Ezek a belső tulajdonságok gyakran a fizika legalapvetőbb elveihez kapcsolódnak. A tehetetlenség az anyagi test belső tulajdonsága, a fény sebessége a foton belső tulajdonsága, a tömeg a részecskék belső tulajdonsága és más hasonló példák. Ahhoz tehát, hogy a fizika tudománya fejlődjön, az ilyen típusú tulajdonságokat fizikailag meg kell magyarázni. Más szóval, a fizikusoknak el kell végezniük a munkájukat.

A problémák még vadabb halmaza fordul elő, ha egyáltalán nincs tárgyi bizonyíték. A modern fizika nem tud határvonalat húzni a fizika és a sci-fi között. A sci-fi és a fantasy szórakoztató gondolkodás, és érdekes könyveket, filmeket és televíziós műsorokat készíthet, de nem tartoznak a fizika komoly vitájába. A fizika jelenlegi tudományos-fantasztikus ágai sok olyan dolgot tartalmaznak, amelyekre nincs fizikai bizonyíték, és bizonyos esetekben nincs lehetőség arra, hogy valaha is létezzen fizikai bizonyíték. A fizikában a tudományos-fantasztikus irodalom leggyakoribb példái a sok világ- és a multiverzum-elméletek.

Mindezek a problémák együttesen valóban nagyon szomorú állapotba hozták a fizikát. Sok fontos és elismert elmélet nyilvánvalóan téves, de a fizikusok semmit sem tesznek ellene. Egyes fizikusok felismerik a problémákat, de nem beszélnek róluk, míg mások együtt működnek az egész leplezésével. A legtöbben jogosan aggódnak a munkájuk miatt, de meg kell felelniük a nyilvánosságnak és a finanszírozást biztosító embereknek. Sokan attól tartanak, hogy életük munkája nem ér semmit. Így továbbra is úgy tesznek, mintha minden rendben lenne az univerzum standard modelljével, abban a reményben, hogy a problémák csodával határos módon majd maguktól megoldódnak.

A fizikusoknak nem sikerült felismerniük a helyzetükhöz kapcsolódó triviális igazságot: a probléma megoldásához először el kell ismerniük, hogy van probléma! Ez az a pont, ahol ez a könyv is képbe jön. A legtöbb fizikus az akadémiai közösségeken belül nem hajlandó elismerni a problémákat, ezért nyilvánvalóan segítségre van szükségük kívülállóktól, fizikusoktól és másoktól, akik nincsenek tudatilag bebetonozva a hivatalos fizika standard modelljébe.

A fizikusok nyilvánvalóan nem hajlandók megkérdőjelezni azt a munkát, amelynek szentelték életüket, még akkor sem, ha tudatuk legmélyén tudják, hogy elméletük túl bonyolult ahhoz, hogy túlélje a fizika közelgő nagy leegyszerűsítését. Senki sem akar a történelem szemétdombján végezni. És mégis, ez fog történni a legtöbbjükkel, ha továbbra sem akarnak tenni ellene semmit.

Azt hallottam, hogy a fizikusok csak akkor fogadnák el, hogy problémák vannak az elméleteikben, amikor már az egész világ nevet rajtuk. 2. Ezért kérjük, csatlakozzon ahhoz a több ezer, a fővonalas fizikától eltávolodott tudóshoz, akik nevetnek rajtuk, miközben a fizika 100 legnagyobb hazugságáról olvasnak. Talán akkor folytathatjuk a fizika egyszerűsítését.

Megjegyzés: A hazugságok nem súlyosságuk szerint vannak rendezve, hanem sorrendben jelennek meg, ami remélhetőleg lehetővé teszi számunkra, hogy meglássuk, hogyan halmozódnak fel a hazugságok egymásra. Mint minden hazugsági próbálkozásnál, egy hazugság egyre több hazugságot szül. Azok a hazugságok, amelyek nem kerültek a legjobb 100 közé, félkövéren vannak szedve, és indexelve vannak a könyv végén. Az előző könyvem, The Zero-Point Universe, jó referencia erre, mivel részletesebben foglalkozik néhány ilyen problémával és a javasolt megoldásaimmal. Tehát, kérem, ne habozzon elolvasni az előző könyvemet vagy az internetet utána nézzen annak!

P.A.M. Dirac, The Evolution of a Physicist’s Picture of Nature , Scientific American 208:5 pp 45-53 (May 1963)

2 F. Bishop, The Science of Censorship, 19 th Natural Philosophy Alliance Conference, Albuquerque, NM, 2012.

1. hazugság: Nincs éter

Az egyetlen egyenlet, amellyel a megfigyelt jelenségeket kielégítően megmagyarázzák, Plancké, és szükségesnek tűnik elképzelni, hogy a rövid hullámok esetében az összekötő kapcsot az anyag és az éter között nem a szabad elektronok, hanem másfajta elektronok alkotják, részecskék, mint Planck-rezonátorok, amelyekre valamiért az ekvipartíciós tétel nem vonatkozik. Valószínűleg ezeknek a részecskéknek olyanoknak kell lenniük, hogy rezgéseiket és az általuk keltett hatásokat ne lehessen megfelelően leírni az elektronelmélet közönséges egyenleteivel; Valamilyen új feltevést kell tenni, például Planck hipotézisét az energia véges elemeiről. 2

Hendrick Lorentz, 1906

A fizikusok hazugságai közül a legnagyobb talán az, hogy nincs éter. A tudományos törekvések kezdete óta a tudósok mindig is azt feltételezték, hogy az űrben van éter, mely a fény és az erők átvitelének közege. Rene Descartes úgy gondolta, hogy a gravitációs erőket éterörvények közvetítik, amelyekről még az 1600-as években úgy gondolták, hogy betöltik a teret, és az éterelmélet a jelen korig velünk maradt.

Az elektromágneses elmélet egyesítése közben James Clerk Maxwell egy örvénnyel töltött étert vizualizált, amely ezen erők és a fény átviteléért volt felelős. 3 A mozgó elektromos töltésekkel kölcsönhatásba lépő és mágneses mezőket létrehozó forgó éter vizualizálása kritikus fontosságú volt az elektromágneses egyenletek és azok egymáshoz való viszonyának megértéséhez. Sajnos ezt a maxwell-i történelemi elképzelést az örvényelméletről, bár technikailag nem helyes, ritkán tanítják az iskolában, és ritkán említik meg a tankönyvekben.

Ugyanilyen szerencsétlenek voltak az olyan rosszul átgondolt kísérletek, mint például Michelson és Morley kísérlete, amelyek kétségbe vonták az 1800-as évek közepének és végének étermodelljét. 4 A korabeli tudósok jártasakká váltak az ideális gázok törvényeinek megértésében, beleértve azt is, hogy a gázok miként lépnek kölcsönhatásba az anyagi testekkel, hogy hőt és energiát adnak át neki. Naivan azt hitték, hogy az éter, bármi legyen is az, hasonlóan ideális gázként fog viselkedni.

Ez felvetette a kérdést, hogy a csillagok és a bolygók hogyan nem párolognak el az éterből átadott hőenergiától? Úgy gondolták, hogy az éter fényellenállást válthat ki, hasonlóan a levegő a hangnál. Ez felvetette azt az ötletet, hogy meg kell tudni mérni a fénysebesség különbségét úgy, hogy az éterhez képest két különböző irányban mérjük a sebességet.

Az éter létezésével kapcsolatos kételyek éppen abban az időben erősödtek meg, amikor Max Planck 1900 és 1911 között egy sor tanulmányban előállt a kvantumharmonikus oszcillátor elméletével. 5, 6, 7 Elmélete kifejtette, hogy egy olyan rendszerben, mint pl. ideális gáz, a gázmolekulák soha nem érik el a nulla energiájú állapotot. Mindig van bennük egy kis maradék energia, még akkor is, ha az összes hőt eltávolítják a rendszerből.

Hendrick Lorentz volt talán az első, aki írásban javasolta, hogy az egyébként üres teret meg lehet tölteni Plank oszcillátorokkal, és ezek az oszcillátorok felelősek lehetnek minden erő hatásáért a tér vákuumán keresztül. 2 Aligha kétséges, hogy ez egy találgatás témája volt közte és kollégája között.

Lorentz azt is felismerte, hogy ezek az oszcillátorok nem követik az ekvipartíciós tételt, ami részben azt jelenti, hogy ezeknek az oszcillátoroknak a mozgása nem járul hozzá a rendszer hőjéhez. Vákuumban a Planck-oszcillátorok miatt nincs melegedés, mivel az oszcillátorok nem adnak át hőenergiát más anyagi testeknek. Megoldódott az a több évtizedes probléma, hogy a bolygókat és a csillagokat miért nem párologtatja el az éter. Kiderült, hogy ez a Michelson-Morley problémát is megoldja.

Így kezdődött az éter modern korszaka, amelyet gyakran vákuum-fluktuációnak, nullponti energiának vagy kvantum-térelméletnek is neveznek. Még Albert Einstein is felvállalta egy ideig ezt a témát, mielőtt bűnbánó étertagadóvá vált volna, mivel Otto Sternnel együtt kitalálta a nullapont energia (németül: nullpunktsenergie) fogalmát egy közösen írt cikkükben. 8 De valójában a gáz nullponti energiájáról írtak akkor, nem a vákuum ingadozásáról.

És aminek fordulópontnak kellett volna lennie a fizikában, a vákuum természetének valódi megértésének korszakának kezdete, mégis rémálommá vált, amikor a vákuum-ingadozás elutasítói péppé zúzták ezeket az elképzeléseket, és végül több mint egy évszázadon át uralták a fizikát. A vákuum fizikai közegének elfogadása nélkül mindenféle képzeletbeli és végső soron helytelen elméleteket dolgoztak ki, hogy megmagyarázzák: miképpen jut át a téren keresztül a fény és az erő.

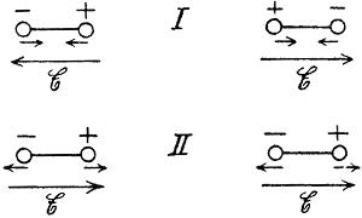
1-1. ábra: Peter Debye szemlélteti a dipóluspárokat, amelyek ellentétes töltésirányokban láthatók, és bemutatja, hogy a dipólusok hogyan hatnak a közeli dipólusokra a töltésorientációjuktól függően.

Aztán a múlt század közepén Hendrik Casimir és Dirk Polder kidolgozott egy elméletet, amely azt jósolta, hogy a vákuum-ingadozások észlelhetőek. 9 Felismerték, hogy a vákuum-ingadozások a van der Waals-erőknek megfelelő módon hatnak egymásra.

A Van der Waals erők az elektromosan töltött dipólusok között fellépő erők összessége. Minden dipólusnak van egy pozitív és egy negatív oldala, és ezek egymásra reagálva oszcillálnak. Peter Debye volt a felelős a van der Waals erő egy típusának felfedezéséért, amelyet az 1-1. ábrán mutat be. 10

1-2. ábra A Casimir-effektus egyszerű illusztrációja két lemez között. Csökken a két lemez közötti erő, mivel a hosszabb hullámhosszú Planck-oszcillátorok ki vannak zárva a lemezek közötti üregből.

Casimir az a felismerése, hogy a vákuum-ingadozások elektromos dipólusként viselkednek, zseniális volt, és megérdemelte volna érte a Nobel-díjat, de sajnos nem kapott. Elméletét egyszerűen megmagyarázza az 1-2. ábrán látható kétlemezes illusztráció. A vákuum-ingadozások az egész térben léteznek, és hullámhosszuktól függően minden méretben előfordulnak. Bizonyos nagyobb hullámhosszak nem férnek el a két lemez közé. Ez nyomáskülönbséget hoz létre a lemezeken a van der Waals erők miatt. Ez az a másik nagy koncepció, amelyet Casimir hirdetett: a vákuum-ingadozások nyomást gyakorolnak az anyagi testekre.

Casimir megjósolta, hogy ez a nyomáskülönbség összenyomja a két lemezt, ami lehet, hogy a legnagyobb hozzájárulása volt a tudományhoz. Közel 50 évbe telt, de a kísérletek végül bebizonyították, hogy Casimir igaza volt. 11,12 Tehát a vákuum-ingadozások nemcsak nyomást gyakorolnak a testre, hanem mozgást is okoznak. És közben nem melegítik fel ezeket a testeket. Az az elképzelés, hogy az éter felmelegíti a testeket, hazugság. Az az elképzelés, hogy az éter kinetikus energiaveszteséget okoz, hazugság.

Évtizedes számítások és kísérletek bebizonyították, hogy a Casimir-effektus valós jelenség, emellett nyilvánvaló lett az is, hogy a Casimir-erők megegyeznek a van der Waals-erőkkel. 13 De ennél is fontosabb, hogy a Casimir-effektus azt bizonyítja, hogy a vákuum-ingadozások valósak. Az éter tehát, az típus, amelyről Planck elméletében írt, valós.

Két másik fontos fogalom: az éter elektromos dipólusokból áll, és ezek a dipólusok a van der Waals-erőknek megfelelően kölcsönhatásba lépnek egymással. A dipólusok is forognak, követve a régi örvényelmélet-leírásokat. Descartes, Maxwell és a többiek, akik egykor a tér éterét örvényként képzelték el, nem voltak olyan messze az igazságtól. Kiderült, hogy az éter még a leírásoknál is egyszerűbb, forgó dipólus.

Sajnálatos módon még ma is, miközben sok fizikus most már felismeri, hogy az éter létezésének tagadása valóban hazugság volt, mégsem jutottak el oda, hogy felmérjék az okozott károkat, és megtegyék a lépéseket az elméleteik kijavítására.

A. Lorentz, The Theory of Electrons, 2nd Edition, B. G. Teubner, Leipzig, G. E. Stechert & Co., New York, 1916, p45. (Taken from a series of lectures presented in 1906.)

3 J.C. Maxwell, “On Physical Lines of Force” Part III “The Theory of Molecular Vortices Applied to Statical Electricity” Philosophical Magazine XXIII, 1862.

4 A.A. Michelson, E. W. Morley "On the Relative Motion of the Earth and the Luminiferous Ether". American Journal of Science 34 : 333–345 1887.

5 M. Planck, Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum, Verhandl. Deutsch. Phys. Ges, p.237 (1900)

6 M. Planck, "Über das Gesetz der Energieverteilung in Normalspektrum." Ann. Physik 4, 553, 1901.

7 M. Planck, "Eine neue Strahlungshypothese," Verhandl. Deutsch. Phys. Ges. 13: 138 (1911)

8 A. Einstein, O. Stern, "Einige Argumente fuer die Annahme einer Molekularen Agitation beim absoluten Nullpunkt" Ann. Phys. 40: 551. (1913).

9 H. B. G. Casimir, and D. Polder, "The Influence of Retardation on the London-van der Waals Forces", Phys. Rev. 73, 360-372 (1948).

10 P. Debye, “Die van der Waalsschen Kohäsionskräfte” Physikalische Zeitschrift,Vol. 21, pages 178-187, 1920.

11 S. K. Lamoreaux, (1997). "Demonstration of the Casimir Force in the 0.6 to 6 μm Range". Physical Review Letters 78: 5. doi:10.1103/PhysRevLett.78.5.

12 U. Mohideen, A. Roy, (1998). "Precision Measurement of the Casimir Force from 0.1 to 0.9 µm". Physical Review Letters 81 (21): 4549. doi:10.1103/PhysRevLett.81.4549.

13 K. A. Milton, The Casimir Effect: Physical Manifestations of Zero-Point Energy, World Scientific, 2001, pg. 79.

2. hazugság: Michelson és Morley megcáfolta az étert

A fizikában a második legnagyobb hazugság az, hogy Michelson és Morley megcáfolta az éter létezését.

Bárki, aki már részt vett fizikaórán, vagy nézett olyan tudományos műsort, amelyben az étert megemlítették, valószínűleg hallotta már ezt a hazugságot.

Természetesen miután elolvastuk, hogy „nincs éter” kijelentés hazugság, nyilvánvaló, hogy a Michelson-Morley kísérlet ezt nem tudta megcáfolni.

Fontos kérdések merülnek fel a kísérlet kudarcával kapcsolatban, többek között:

1. Miért nem sikerült a kísérlet?

2. Mi volt a rossz a kísérlethez vezető feltevésekben?

3. Mit bizonyított valójában a kísérlet?

Ahhoz, hogy kitaláljuk, mi ment rosszul, meg kell vizsgálnunk Maxwell sejtését, mivel az éterről és a fényről alkotott elképzelései vezettek a kísérlethez. 14

Sejtése az volt, hogy éterellenállás van a fényben, és mivel a Föld az éterhez képest mozog, úgy gondolta, hogy ez a ellenállás a fénysebesség változásaként érzékelhető.

A kísérletet ezután úgy tervezték meg, hogy a fény sebességét két irányban, egymással 90 fokos szögben mérjék.

A kísérlet egyik vicces figyelmen kívül hagyása az volt, hogy azt gondolták, hogy a Föld sebességét látják a Naphoz viszonyítva, nem pedig a Napot a galaxishoz viszonyítva, vagy még inkább a galaxist az éter nyugalmi állapotához viszonyítva.

A Föld sebességét az éter nyugalmi állapotához viszonyítva valóban meg tudnák mérni, ha az éterellenállás valós lenne, de csakis akkor.

Folytatva tehát, az éter-ellenállás ötlete azért merült fel, mert Maxwell és mások úgy gondolták, hogy a fény az éteren keresztül hasonló módon terjed, mint a levegőben haladó hang. Gondoljon bele: egy autó által kibocsátott zaj magasabb hangerővel jön feléd, mint ahogy elhajt. Ez a Doppler-effektusnak köszönhető. A hangsebesség sokkal gyorsabb, mint a legtöbb szél a Földön, de az egyenletes hátszél lehetővé teszi a hang egy kicsit gyorsabb terjedését, az állandó szembeszél pedig egy kicsit lassítja a terjedést. Ennek az az oka, hogy a hangsebesség a levegő nyugalmi állapotához viszonyítva többé-kevésbé állandó. Az oldalszél a hang lelassulását is okozza a csendes levegőben tapasztalható terjedési sebességhez képest, amint az a következő ábrán látható.

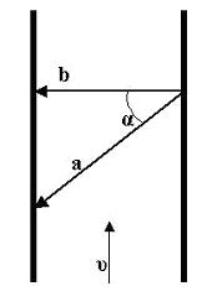
2-1. ábra. Egy fénysugár keresztezi két falat a b út mentén, de az éter iránya és a nyíllal jelzett υ sebesség miatt az effektív távolság a . A két út között az α szög látható.

Fontos megjegyezni azt is, hogy a fénysebesség Maxwell elméletében az éter nyugalmi állapotában mérve éri el a maximumát. 14 Maxwellt tartják az elsőnek, aki felismerte ezt a tényt. Ha egy megfigyelő, például a Földön, az éter nyugalmi állapotához képest mozog, a fénysebesség ebben a vonatkoztatási rendszerben lassabbnak tűnik, ha az éter nyugalmi keretben lévő megfigyelő látja. Erről később lesz még szó. A mozgó nyugalmi keretek közötti mérések transzformációinak végrehajtásával foglalkozó tudomány a relativitás elnevezést kapta. A fizikusoknak a kísérlet idején nem volt megfelelő felfogásuk a relativitáselméletben, ami sok tévhithez vezetett.

A Michelson-Morley kísérlet kimutatta, hogy az éternyomás klasszikus fogalma hazugság. A kísérlet nem vallott kudarcot, a kezdeti feltételezések voltak tévesek. A fizikusok félreértelmezték az eredményeket, ezért úgy döntöttek, hogy nincs éter - pedig az eredmény értelmezésének helyes módja az lett volna, ha kimondják: Maxwell sejtése téves volt.

Elgondolkozott már azon, hogy a Michelson-Morley-kísérlet előfeltétele miért az éter létezésének tesztelése volt, de a válasz rá a relativitáselmélet állapottranszformációs egyenlete?

Az egyik fontos dolog, amit a Michelson-Morley-kísérlet kapcsán meg kell jegyezni, hogy a fényforrás és a detektorok ugyanabban a referenciaállapotban vannak, így minden feltételezett állapottranszformációs séma esetén magának a készüléknek nincs szükség állapottranszformációra.

Ennek ellenére a fényfotonoknak saját nyugalmi állapotuk van, az éter-nyugalmi állapotuk. Elképzelheti magát, ahogy fénysebességű fotonon lovagol. Maxwell elmélete szerint ekkor fénysebességgel utazna az éter nyugalmi állapotához képest. Az éter nyugalmi állapotát tekinthetjük a természetes foton-referencia állapotnak, és az éter nyugalmi állapotában lévő foton energiája a természetes energiája.

Maxwell sejtésének fő hibája az volt, hogy azt gondolta, hogy a foton sebességváltozásai a forrás sebességétől függenek az éter nyugalmi állapotához viszonyítva. A detektor sebessége azonban nem számít. Hazugság azt állítani, hogy a fény a fényforrás vonatkoztatási rendszerében halad.

Az éter maga az éter nyugalmi állapotából nézve minden irányban egyenletes, így a fotonok sebessége szintén minden irányban egyenletes. Nincs irányfüggés a fénysebességtől, mivel a fotonok mindig az éter nyugalmi keretben haladnak, aminek nincs irányfüggése. A fénysebesség irányfüggésének a fogalma hazugság.

Ha egy mozgó detektor szemszögéből látjuk az éterellenállást, azt nem a sebességeltolódásban látjuk; energiaváltásnak tekintjük. A Michelson-Morley kísérlet nem mutat energiaeltolódást, mert a forrás és a detektor ugyanabban a vonatkoztatási rendszerben van.

Tehát mit igazolt valójában ez a kísérlet? Bebizonyosodott, hogy:

1. A fizikusok nem ismerték fel, hogy a fény mindig az éter nyugalmi állapotában halad, függetlenül a forrás sebességétől.

2. A fizikusok nem ismerték fel, hogy a fény sebessége független az iránytól.

3. A fizikusok nem tudták, hogyan kell helyesen végrehajtani és értelmezni a relativisztikus kerettranszformációkat.

4. A fizikusok nem tudták, hogy a megfigyelő sebessége az éter nyugalmi keretéhez viszonyítva a sebességváltozások helyett a vörös- vagy kékeltolódásokért felelős energiaváltozásokat okozza.

5. A fizikusok nem ismerték fel, hogy Maxwell éternyomásról alkotott elképzelése téves.

6. A fizikusok nem ismerték fel, hogy Maxwell sejtése téves.

Mivel a fény mindig az éter nyugalmi állapotában halad, a relativisztikus transzformációk csak a mozgó forrás vagy detektor hatásainak magyarázatához szükségesek.

Sajnos néhány fizikus továbbra is teszteli Maxwell sejtését, és megismétli a Michelson-Morley-kísérletet, még akkor is, ha sejtése téves volt, és téves volt az az elképzelés is, hogy a fény a forrás referenciakeretében halad.

Az az állítás, hogy Michelson és Morley megcáfolta volna az étert, hazugság.

Tehát mi történik valójában a fénysebességgel? Nos, ezzel egy csomó más hazugságba keveredünk.

J. C. Maxwell, “On a Possible Mode of Detecting a Motion of the Solar System Through the Luminiferous Ether” Nature, 1880, Vol. XXI, pp. 314, 315.

15 C. Lineweaver, et al. "The dipole observed in the COBE DMR four-year data'" Astrophysics J. 470, 38,1996.

3. hazugság: Hullám-részecske kettősség

Egy óceánjárónak különösképpen az a tapasztalata, hogy az óceán inkább hullámokból áll, mint vízből. 16

Sir Arthur Eddington, 1927

A fizikában a harmadik legnagyobb hazugság a hullám-részecske kettősség. A hullám-részecske kettősség fogalmának tanítása már az általános iskolai fizikaórákon elkezdődik, és népszerű tudományos műsorokban, magazinokban és weboldalakon terjesztik. A tanárok azt a dogmát tanítják, hogy a részecske nem csak részecske, hanem hullám is. Azt mondják, hogy néha könnyebb részecskeként kezelni, néha pedig jobb hullámként tekinteni. Ismét félrevezettek minket a vákuum-ingadozást elutasító tényezők.

Hogy történhetett ez?

Kezdeti hasonlatként gondolhatunk hullámokra a vízben vagy hanghullámokra a levegőben. A vízen áthaladó csónak hullámot hoz létre. De a csónak nem hullám; a csónak csak egy csónak. A hullám vízből áll. Először a csónak nyomja a vizet, majd az a víz még több vízre van hatással. A tényleges hullámok teljes egészében vízből állnak.

Nincs hullám-hajó kettősség.

A hanghullámok hasonlóak. Képzeld el, hogy megkongatnak egy harangot, amely rezeg, és hangokat küld a levegőbe. A harang nem hullám; a harang csak egy harang. Amint rezeg, a szomszédos levegőnek nyomódik, majd ezek a levegőmolekulák más levegőmolekuláknak nyomódnak. A hanghullámok a levegő sajátosságai.

Nincs hullám-harang kettősség.

Szóval hogyan torzították el a fizikusok ennyire a dolgokat?

Képzeljen el egy olyan furcsa bolygót, mely hasonlítana a miénkhez, de a lakói nem látnák és nem éreznék az óceánok vizét. Láthatnák a halakat, csónakokat és különféle úszógumikat furcsán felfüggesztve, de a vizet nem. Aztán egy józan elméjű fiatal fizikus mintákat vett észre a csónakok és halak alatti homokban, és felismerte, hogy ezek a minták bizonyos tulajdonságokkal rendelkeznek, mivel hullámosak és interferenciamintákat mutatnak.

Ja és mellesleg, amikor valaki azt javasolta, hogy van egy anyag, amit „víznek” nevezett, mint lehetséges oka ezeknek az interferencia-mintáknak, a világ vezetése kimondta, hogy nincs olyan, hogy víz, mivel az láthatatlan, és egy híres tudós egyszer kísérletet végzett, hogy megcáfolja létezését.

Honnan erednek tehát ezek a hullámzó fodrozódások – kérdezné a mi fiatal fizikusunk? Tudom, azt gondolná, hogy a halak, a csónakok és a vízen hányódó törmelékek nem pusztán anyagtestek, hanem hullámok is kötődnek hozzájuk, mint az alkotóelemük, ezért néha egy csónakot vagy halat hullámként kell kezelni, hogy megmagyarázza a homok hullámait. Úgy gondolná, hogy ezek a hullámok minden csónakból és halból kifelé nyúlnak. Ezek a hullámtulajdonságok kölcsönhatásba léptek egymással, és összetett mintákat alkottak a homokban, mégsem látná a hullámokat.

A Föld bolygó fizikusai is nagyjából ilyenek. Megvizsgálták a részecskéket és a mozgásuk által előidézett hullámjelenségeket, és kíváncsiak voltak arra, honnan származnak a hullámtulajdonságok. De vákuum-ingadozás és éter-elutasítók lévén, mit tanítottak is nekik, megrekedtek ebben a szemléletben. Így mivel nem volt közeg a hullámok továbbítására, azzal az őrült ötlettel kellett előállniuk, hogy a részecske egyszerre részecske is, meg hullám is.

Ekkor született meg a hullám-részecske kettősség nevezetű hazugság. Először a fizikusok elutasították az éter létezését, ami olyan lenne, mint egy hajóskapitány, aki tagadná a víz létezését, vagy egy zenész, aki tagadná a levegő létezését, de mégis meg kellett kérdezniük: honnan jönnek ezek a hullámok? Meg voltak győződve arról a hazugságról, hogy a tér üres, és ezért elakadtak abban, hogy megmagyarázzák, hogyan tud egy hullám áthaladni az üres téren. Ezért úgy döntöttek, hogy a legegyszerűbb kiút ebből a problémából az, ha mindenkit elhitetik azzal, hogy a hullám a részecske sajátossága, és a részecske valahogy végtelenül átnyúlik a térben hullámjelenségeket generálva. Máskor pedig a részecske csak egy részecske, és úgy viselkedik, mintha nagyon kicsi lenne.

Természetesen az igazság sokkal egyszerűbb. Léteznek vákuum-ingadozások. Az egész teret betöltő éter valódi. Ez az éter, amint azt az 1. fejezetben is tárgyaltuk, elektromos dipólusokként viselkedik, amelyek a mozgó töltésekre reagálva mozognak. Épp úgy mozgó anyagtestekre reagálva is mozognak, amiről később még részletesebben is szó lesz.

Ahogy a részecskék a térben mozognak vagy forognak, a közeli vákuum ingadozásait mozgatják és forgatják. Ezek viszont más vákuum-ingadozásokat okoznak, hogy mozogjanak és forogjanak. Nagyon gyorsan hullámjelenségek láthatók a vákuum-ingadozások tengerében, amint kölcsönhatásba lépnek más részecskékkel vagy anyagtestekkel.

A helyzet valamivel bonyolultabb, mint a hanghullámok a levegőben vagy a hullámok a vízben, mivel a vákuum ingadozása nem látható közvetlenül, és a dipólus kölcsönhatások valamivel összetettebbek. Olyan ez, mint a kitalált bolygó a láthatatlan vízzel, amely semmihez sem hasonlít. Csak a hátrahagyott bizonyítékokat látjuk.

A hullám-részecske kettősség hazugság. A részecske csak egy részecske. A hullámok éterből, az éter pedig részecskékből áll, így a végén még a hullámok is részecskékből állnak.

16 A. Eddington, Gifford előadása az Edinburghi Egyetemen, 1927. március, The Nature of the Physical World, 1929, reprint 2005, 242. oldal.

4. hazugság: A fotonok elemi részecskék.

A fizika negyedik legnagyobb hazugsága, hogy a fotonok elemi részecskék. Több mint 100 éve a fotonokat elemi részecskéknek tekintik, így ez a hazugság a legtöbb embert meg fogja lepni. Minden tankönyv és minden részecsketáblázat ezt mondja, és minden fizikaórán, népszerű műsorokban és irodalomban megismétlik. Amit azonban nem mondanak el, hacsak nem ásunk mélyebbre a tudományban, az az, hogy van a fotonnak egy alapvetőbb modellje, amely legalább az 1930-as évek óta létezik. Azok, akik alapvető kvantumtérelméletet vagy Feynman-diagramokat tanulnak, valószínűleg találkoznak vele, de a legtöbben nem veszik figyelembe a fontosságát.

A fizika tanításában van egy olyan ellentmondás, amely a foton legalapvetőbb leírásával kezdődik. A fotonokat következetesen elemi részecskéknek nevezik, ugyanakkor azt mondják, hogy elektromos és mágneses tereket hoznak létre, és hullámtulajdonságokkal rendelkeznek. Az elektromos és mágneses mező tulajdonságai, valamint a hullámtulajdonságok igazak, mivel összhangban vannak a kísérleti megfigyeléssel.

Az első dolog, amit észre kell vennünk, a hullámok problémája. Ahogy az az utolsó fejezet után várható volt, a fizikusok hazudtak a fotonok hullám-részecske kettősségéről. Azt mondják, hogy a fotonrészecske egy része varázsütésre olyan hullámot hoz létre, amely a végtelenségig terjed. Ez a hullám előidézi a számunkra oly ismerős interferenciamintákat és egyéb jelenségeket. De mivel tudjuk, hogy az éter létezik, a hullámoknak is éterből kell állniuk, és a részecske csak egyfajta részecske, vagy talán valami, ami csak úgy néz ki, mint egy részecske.

Ami a leírás másik részét illeti, az a kérdés, hogyan hoz létre egy foton elektromos és mágneses teret? A fizikusok nem mondják el, ahogy persze nem is tudják, hiszen nem ismerték fel a fontosságát, amikor szóba került az órán, vagy könyvben olvasták.

Noha ismert, hogy a fotonok elektromos és mágneses teret hoznak létre, általában elektromosan semlegesnek tartják őket, és igaz, hogy a fotonok nettó töltése nulla. De hogyan hoz létre egy nulla töltésű részecske forgó elektromos és mágneses teret? Biztos fizikai varázslat.

A fizikusok még ennek megválaszolása nélkül is ragaszkodnak ahhoz, hogy a fotonok elemi részecskék. Talán néhányuk közülük időről időre megkérdőjelezik a mezők és hullámok mágikus terjedésének gondolatát, de ezt a kételyt gyorsan elvetik maguktól, mivel káros lenne mindenféle jelenleg uralkodó fizikaelméletre, mint azt látni fogjuk. Főleg ha nyilvánosan teszel fel ilyen a kérdést, vagy ami még rosszabb: meg is próbálsz válaszolni rá, akkor rögtön a fizikus közösség kórusát hallhatod, hogy áltudományos fantasztának bélyegez!

Ha figyelmen kívül hagyjuk az összes dogmát és tudománypolitikát, szembe kell néznünk a kérdéssel; hogyan hoz létre egy foton forgó elektromos és mágneses teret? Az az elképzelés, hogy az elektromos és mágneses mezők a fotonok velejárói, nyilvánvaló hazugság. Kiderült, hogy az elektromos mező létrehozásának legegyszerűbb módja az elektromos töltési dipólus. Az elektromos dipólus egyik végén pozitív, a másik végén negatív töltés van. Ha ezek a töltések ellentétesek, de egyenlők, a dipólus távolról még mindig elektromosan semlegesnek tűnik.

A foton elektromos tere idővel változik, lassan egy irányban erősödik, amíg eléri a csúcsot és gyengül, majd negatív lesz, tetőzik és nullára tér vissza. Minden hullámhosszon egyszer végigmegy ezen a cikluson. Ez a hatás akkor érhető el, ha forgó dipólusai vannak, ahol az első egy irányba, a második pedig a másik irányba forog. Ily módon egy sor forgó dipólus hozza létre azt a forgó elektromos teret, amelyet egy fotonból látunk.

Ha egy dipólus forog, akkor mágneses mezőt is hoz létre, így a forgó dipólus egyidejűleg oszcilláló mágneses teret létrehoz, amely az oszcilláló elektromos térrel is együtt jár.

Kísérleti bizonyítékok igazolják, hogy a foton minden egymást követő fél hullámhossza alatt az elektromos és a mágneses mezők ellentétes irányúak. Következésképpen minden egymást követő dipólust az előző dipólussal ellentétes irányba kell orientálni. Ez a mozgás tagadja az előző dipólus impulzusimpulzusát, így a foton nettó nulla impulzusmomentumot ad.

A foton elektromos és mágneses mezőjének fizikai modellezésének legegyszerűbb módja, ha az egy sor forgó dipólusból áll, és minden fél hullámhosszon megjelenik egy-egy új dipólus, ahogy az a 4-1. ábrán látható. Az éterhullámon kívül ez az alapja a foton összetett részecskeként való valódi alapvető leírásának.

4-1. ábra Foton, mint forgó dipólusok sorozata, amelyek forgó elektromos és mágneses tereket hoznak létre.

Az az elképzelés, hogy az elektromos és mágneses mezők egy forgó dipólus eredménye, teljesen nyilvánvaló és nem új. Az 1930-as évek elején, röviddel azután, hogy Anderson felfedezte a pozitront, nyilvánvalóvá vált, hogy egy foton virtuális elektron-pozitron párok sorozatából áll. Mindegyik fél hullámhosszon van egy virtuális elektron-pozitron pár.

Ebben az esetben a „virtuális” kifejezés azt jelenti, hogy az elektron-pozitron pár inkább vákuum fluktuáció, mint hosszabb élettartamú részecskepár. Ez azért fontos, mert a fotonnak nincs tömege, a hosszabb élettartamú részecskepárnak pedig van tömege, míg a vákuum-ingadozásnak nincs. Elvileg bármilyen fizikailag valós virtuális részecskepárból lehet fotont készíteni, amely elektromos dipólust alkot. Ne feledje, hogy a „virtuális” szó ebben az esetben és ebben a könyvben semmiképpen sem jelenti azt, hogy a részecskepár nem valódi.

A foton elektron-pozitron modelljét nemrégiben Richard Feynman népszerűsítette, és néha a Feynman-diagramokon is látható. 17 A 4-2. ábrán egy foton balról jobbra halad, amit egy hullámvonal ábrázol, az elektron-pozitron párt pedig az ovális ábrázolja. Az elektron a fotonnal megegyező irányba mozog, míg a pozitron az ellenkező irányba.

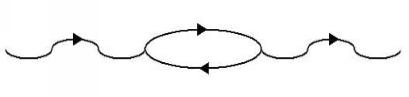
kép 4-2. ábra Virtuális elektron-pozitron pár egy foton részeként (nem méretarányosan).

Ahhoz, hogy megbizonyosodjunk arról, hogy egy foton vákuum-fluktuációs modellje megfelelő, figyelembe kell vennünk a foton minden fél hullámhosszának energiáját is. Ez az energia történetesen Planck állandó szorozva a frekvenciával osztva kettővel, ami szintén Planck energiája egy kvantumharmonikus oszcillátorhoz, egy vákuum-ingadozáshoz. Történetesen ez a Heisenberg-féle bizonytalansági elv szerinti maximális energia is, amely lehetővé teszi a dipólus létezését, de nem minden tulajdonsága egyszerre detektálható. Vegye figyelembe, hogy a mező a teljes energia felét hordozza, különválva a dipólustól, de ezt az energiát gyakran figyelmen kívül hagyják.

A fotont alkotó dipólusok, amelyek a forgó elektromos és mágneses mezők létrehozásáért felelősek, vákuum-ingadozások. Minden egymást követő vákuum-ingadozás megjelenik a vákuumban, és eltűnik a vákuumban. Minden vákuumfluktuációs dipólus a vákuumból indukálódik, megőrizve az energiát és a lineáris impulzust, és minden egymást követő dipólus ellentétes irányba forog, így a szögimpulzus megmarad.

A fotonnal együtt terjedő elektromos és mágneses hullámok összetételének kérdése könnyen megválaszolható. Ezek a hullámok áthaladnak és az éterből, a vákuum-ingadozásokból állnak. Minden virtuális dipólus, amely a foton részét képezi, a szomszédos vákuum-ingadozásokat elforgatja. Azok a vákuum-ingadozások befolyásolják a mellettük lévőket. Ezek a hullámszerű kölcsönhatások aztán a végtelen felé terjednek.

Teljesen világos tehát, hogy a fotonok nem alapvető részecskék, mivel őket egy alapvetőbb elvre lehet visszavezetni. A fotonok teljes egészében éterből álló összetett részecskék. A fotonok vákuum-ingadozásokból állnak, és nem mások, mint az energia vákuumon keresztüli szállításának eszközei. Nemcsak, hogy nem alapvetőek, de a hazugság még nagyobb, hiszen nem is részecskék.

A teljesség kedvéért megfontolhatjuk, hogy a fotonok más típusú vákuum-ingadozásokból is létrejöhetnek, nem csak virtuális elektron-pozitron párokból. Bármely valós virtuális részecskepár, amely nem nulla elektromos töltéssel rendelkezik, megfelel ennek. Általánosabban tehát azt mondhatjuk, hogy a fotonok bármilyen valós virtuális részecskepárból állhatnak. A „valódi” kifejezés itt valódi elemi részecskét jelent, nem pedig összetett vagy kitalált részecskét.

Azt is fontos megjegyezni, hogy a virtuális részecskepárok nem léteznek elég sokáig ahhoz, hogy nyugalmi tömegük legyen, tehát ez nem probléma. A foton összetett modelljének nincs nyugalmi tömege, akárcsak a foton mostani elképzelésének. De a tömegről a későbbiekben még lesz szó.

Hogyan történhetett ez a hazugság? Miért tartják fenn ezt a hazugságot, miközben létezik egy alapvetőbb modell? Nehéz kérdések ezekre válaszolni egy fizikusok számára.

Végső soron fizikusként nincs más választásunk ebben a kérdésben. A forgó elektromos és mágneses mezők fizikailag valóságosak, és tudományunk megköveteli, hogy találjunk rájuk fizikai magyarázatot. Nem hagyhatjuk figyelmen kívül őket, és nem mondhatjuk, hogy nem szeretjük az elmélet vagy a matematika működését. Egy elméletet működésbe kell hoznunk.

Az az állítás, hogy a fotonok alapvetőek, hazugság. Összetett részecskéknek kell lenniük, mellyel így megmagyarázhatók a forgó elektromos és mágneses mezők.

17 P.W. Milonni, The Quantum Vacuum, Academic Press LTD, London 1994, p. 49.

5. hazugság: Virtuális fotonok

A fizikában az ötödik legnagyobb hazugság a virtuális foton. A virtuális foton a vákuum ingadozásának egy fajtája, amely fényfotonból jön létre. Ez az egyik legnagyobb hazugság, amely lelassította az éterelmélet megértésének folyamatát. Az utolsó fejezet alapján már nyilvánvalónak kell lennie néhány oknak, amiért a virtuális fotonok nem valósak.

A legtöbb vákuum-ingadozási elmélet részecskepárként modellezi őket, amelyek a vákuumból előállíthatók, majd megsemmisülnek és visszakerülnek a vákuumba. Ezek a részecskepárok teljesítik a Planck-energiafeltételt, és nem lépik túl a Heisenberg-határértéket. Minden virtuális részecskepár egy anyagrészecskéből áll, valamint a vele ellentétes antianyagrészecskéből. A fotonokról azt mondják, hogy önmaga antirészecskéje, tehát egy virtuális foton az két foton. Ez rávilágít egy másik hazugságra: ha a fotonok nem részecskék, akkor a fotonok antirészecskék sem lehetnek.

Amikor a vákuum energiájának modellezéséről van szó, a fizikusok általában az általuk ismert legalapvetőbb részecske, a foton segítségével modellezik azt. Ezért a virtuális fotonokat gyakran a nullponti energia alapvető formájának tartják. Ez a helytelen feltételezés nagy probléma a fizika számára.

Míg a fotonoknak van elektromos és mágneses tere, távolról nézve ezek a mezők elektromosan semlegesnek tűnnek. A virtuális fotonokat ezután elektromosan semlegesnek tekintik. Ennek ellenére néhány fizikus elég okos ahhoz, hogy felismerje, hogy az elektromos és mágneses mezők miatt a fotonok továbbra is dipólusként kezelhetők, és továbbra is a van der Waals-erőknek megfelelő módon hatnak egymásra. Az elméletek túlnyomó többségében azonban figyelmen kívül hagyják a virtuális fotonok dipólus jellegét.

A probléma valódi mélységének megértéséhez meg kell vizsgálnunk egy virtuális fotonpár energiáját. Ha figyelembe vesszük a vákuumból felbukkanó két foton energiáját, amelyek egy teljes hullámhosszon kifelé és egy másik teljes hullámhosszon visszafelé léteznek, akkor 4hν kombinált energiát kapunk, ahol h Planck állandója, ν (a görög nu betű) pedig a frekvencia. A virtuális részecskék azonban nem haladhatják meg a ½hν-t, mivel ez a Planck-oszcillátor energiája, és Heisenberg szerint az idő-energia határértéke, szem előtt tartva, hogy van még ½hν a mezőben. Ezért egy virtuális foton nem állhat két teljes hullámhosszúságú fotonból.

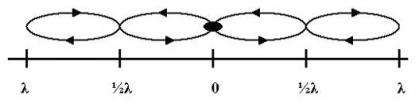
5-1. ábra Vákuumfluktuáció, mint egy fotonpár, amely a központból indul ki, és mindegyik foton egy teljes hullámhosszt kifelé, majd egy teljes hullámhosszt visszafelé halad. A nyilak a terjedés irányát mutatják. (Lambda a hullámhossz szimbóluma.)

Következőről van szó: a fotonpár minden fele kimegy egy fél hullámhosszon, majd visszatér. Ebben az esetben a virtuális foton energiája 2hν, ami még mindig túl sok. Ahelyett, hogy ki- és visszatérnénk, úgy képzelhetnénk el a virtuális fotont, mint két fél hullámhosszúságú fotont egymás mellett, de valahogy nem térnek vissza. Ebben az esetben az energia továbbra is hν lesz és nem ½hν.

Ha ehelyett két negyed hullámhosszúságú fotonra próbálunk eljutni, ezek nem létezhetnek. A negyed hullámhosszú reflektor megakadályozza, hogy ez a hullámhossz az üregben létezzen, mivel interferál önmagával. A negyedhullámú bevonatokat például lencsékben használják a visszaverődés megakadályozására.

Ahhoz, hogy legyen egy Planck-energiával rendelkező virtuális foton, egyetlen fél hullámhosszú fotonnak kell lennie, és egyáltalán nem fotonpárnak. Ebben az esetben azonban nem lehet fotonpár-termelést vagy fotonpár-megsemmisítést végezni, mivel nincs fotonpár. Ha nincs ellenpár, az nem vákuum-ingadozás, hiszen nem nulla energiával kezdődik és végződik. A virtuális foton egyetlen fotonmodellje így kudarcot vall az energiamegmaradási teszten.

Szerencsére van egy egyszerű kiút ebből a rejtélyből. Amint azt az utolsó fejezetben tárgyaltuk, a fél hullámhosszú fotont alapvetően részecskepár dipólusként írják le, például virtuális elektron-pozitron párként. A virtuális elektron-pozitron pár lehetővé teszi a párok létrehozását és megsemmisítését, és megfelel a vákuum-ingadozás energiahatárainak. Nem meglepő, hogy a foton elektron-pozitron modellje egyben a virtuális foton megfelelő alapvető leírása is, amely valójában nem is foton.

5-2. ábra Vákuum fluktuáció egyetlen fél hullámhosszú fotonként. A nyilak a terjedés irányát mutatják.

Furcsa, hogy a fizikusok virtuális fotonokról beszélnek, de nem hajtanak végre alapvető ellenőrzést annak megállapítására, hogy valóban létezhetnek-e. Egyszerűen belátható, hogy minden életképes fotonpár-modell túl sok energiával rendelkezik ahhoz, hogy valódi vákuum-ingadozás jöjjön létre.

Csakúgy, mint a fotonok esetében, a virtuális fotonok, kiterjesztve a létezésüket, bármilyen valós virtuális részecskepár lehet. És igen, tömeg nélküliek, mivel nem haladják meg a Planck-energiát.

A virtuális foton fogalma hazugság. Az éterfizika sokkal gyorsabban fejlődne, ha a fizikusok csak ezt az egyszerű tényt ismernék fel.

A 6. nagy fizika hazugság az éter a virtuális fotonok.

Ez a hazugság természetesen a 4. és az 5. hazugság egyenes következménye. Valahogy minden erőt át kell adni az éteren keresztül, ezért az éter összetételének megértése elengedhetetlen az erők működésének megértéséhez. Mivel a fizikusok helytelenül írták le az étert, ha éppen nem azzal voltak elfoglalva, hogy teljesen figyelmen kívül hagyják a létezését, megállították annak a kibontakozását, hogy az erők elméletét jobban megértsük.

Azoknak a fizikusoknak, akik nem teljesen figyelmen kívül hagyták az étert, meg kellett határozniuk a vákuum-ingadozások modellezésének legjobb módját. Annak érdekében, hogy ne sértsük meg az energiamegmaradás elvét, a vákuum-ingadozásoknak nulla energiával kell kezdődniük és végződniük, és nem haladhatják meg a Planck-féle energiahatárt. Eddig az egyetlen módja annak, hogy a vákuum-ingadozásokat úgy modellezzük, hogy előtte és utána nulla energia legyen, az az, hogy feltételezzük, hogy anyag-antianyag részecske párok. Ezek a párok együtt jönnek létre, és megsemmisítik egymást. A modellnek ez a része egyszerű.

A következő lépés annak eldöntése volt, hogy milyen egy vagy több típusú részecskepárok alkotják az étert. A mainstream fizikusok helytelenül választották a fotont, mivel azt gondolták, hogy ez a legalapvetőbb éterrészecske. A fotonról tévesen azt is gondolták, hogy a saját antirészecskéje, holott egyik sem részecske valójában. Tehát a fizikusok elrontották a dolgot, és úgy döntöttek, hogy a vákuumot virtuális foton-antifoton részecskepárokként modellezik.

Mivel a fotonokat nagy léptékben tekintve elektromosan semlegesnek tekintik, az étert is elektromosan semlegesnek tekintették. A legtöbb fizikus nem gondolt arra a lehetőségre, hogy az éter dipólusként működik, még Casimir javasolta után sem. Ó, ha egyszer is belegondolnának, rájönnének, hogy mivel a fotonoknak forgó elektromos és mágneses mezője van, legalábbis dipólusként viselkednek, de nagyon kevés munkát végeztek annak érdekében, hogy a fotonok dipólus jellegének következményeit feltárják.

A nullpont-térelmélet elsorvadt a virtuális fotonmodell mellett. Annak ellenére, hogy a fotonok elektromos és mágneses tereket hoznak létre, nem gondolták, hogy jelentős mértékben hozzájárulnának az elektromágneses erőelméletekhez, csak mint mérőbozon vagy erőhordozó, egy olyan részecske, amely valamilyen módon felelős az erők kommunikálásáért. Ami az erős, gyenge és gravitációs erőket illeti, a virtuális fotonokról azt gondolták, hogy csak kis mértékben vesznek részt a kölcsönhatásokban, ha egyáltalán részt vesznek.

Ha a foton éppen nincs útban, akkor az elektron és a szemközti antianyaga, a pozitron, a legalapvetőbb részecske.

Ezenkívül tartósan stabilak, ami nagyon különlegessé teszi őket, mivel csak két részecske az. Noha létezik egy egyenlet, amely leírja az elektron egyes jellemzőit, a Dirac-egyenlet, de jelenleg nincs olyan fizikai leírás az elektronról, amely másnak tenné, mint elemi részecske.

Lehetséges, hogy a vákuum-ingadozások valójában nem elektron-pozitron párok, hanem inkább az elektronok és pozitronok előfutárai. A szabad és stabil elektronoknak és pozitronoknak van tömegük, míg a vákuum-ingadozásoknak nincs. Ez két fontos kérdéshez vezet; hogyan történik ez, és mi a tömeg? A tömegkérdésekkel később foglalkozunk. Egyelőre elég annyit mondani, hogy amikor virtuális elektron-pozitron párokra gondolunk, valami elektronszerű és pozitronszerű dologra kell gondolnunk, ami nem feltétlenül azonos e részecskék tartósan stabil változataival. Kezdetben a legfontosabb tulajdonság az, hogy anyag-antianyag párok, amelyek elektromos töltési dipólusokat alkotnak.

A szimmetria és a későbbiekben kifejtendő egyéb érvek miatt is kell lennie egy olyan dipólusnak, amely egy anyag-antianyag részecske párt alkot, ahol az anyagrészecske pozitív, az antianyag részecske pedig negatív töltésű. Az anyag és a töltés tulajdonságait tekintve azt mondhatnánk, hogy az ilyen típusú virtuális részecskepár protonszerű és antiprotonszerű. Ez nem jelenti azt, hogy azok tényleges protonok és antiprotonok. Egyelőre elég ennyi, mert még visszatérünk ehhez a témához, miközben további nagy hazugságokat tárunk fel.

A virtuális fotonokból álló éter hazugság. Ha felismerjük, hogy az éter részecskepár-dipólusokból áll, azonnal láthatjuk, hogyan lép kölcsönhatásba az éter az anyagtestekkel. A Casimir-erő csak a tudás jéghegyének csúcsa, amely csak arra vár, hogy meghódítsák. Azt is látni fogjuk, hogy a dipoláris éter létezése megköveteli számos elmélet megváltoztatását, hogy hozzáidomuljon a jelenlétéhez.

7. hazugság: A fotonok erőhordozók

A 7. nagy fizikai hazugság, hogy a fotonok erőhordozók. Az erőhordozókat mérőbozonoknak nevezik, ezért gyakrabban mondják, hogy a fotonok mérőbozonok. A mérőbozonok a szabványos modellben részecskék, amelyek felelősek az erőkkel kapcsolatos információk továbbításáért. Két részecske vagy anyagtest kicseréli ezeket a részecskéket a kommunikáció érdekében.

Ez az elképzelés abból az alapvető problémából fakad, amelyet a vákuum-ingadozást elutasítók magukra hoztak. Vákuumingadozásokkal teli éter nélkül a vákuumnak nincs olyan közege, amely felelős lenne az erőátvitelért. A vákuum ingadozása nélkül a visszautasítóknak varázsütésre távol maradt akciójuk. Tehát annak érdekében, hogy egy kicsit kevésbé tűnjenek varázslóknak, és inkább tudósoknak, kitalálták azt az ötletet, hogy az erőket mérőbozonoknak nevezett részecskék hordozhatják. Megtették a fotont az elektromágneses elmélet mérőbozonjává, az elektromos és mágneses erők erőhordozójává.

Ez azonban csak egy enyhe trükk, amely áthelyezi a problémákat, nem pedig megoldja őket. Ezenkívül új, még rosszabb problémákat vet fel. Amint azt a mérőbozonokkal kapcsolatos problémák áttekintése után látni fogjuk, ez valóban megkérdőjelezi a fizikusok kritikai gondolkodási képességét.

Először is, a foton energiája, hullámhossza és frekvenciája nem független. A foton az irányon kívül egy bit adatot hordoz, ami nem elég információ ahhoz, hogy erőhordozóként működjön. A virtuális fotonnak lehet hullámhossza és iránya, de a Heisenberg-féle bizonytalansági elv kiterjesztésével nem lehetséges mindkettőt egyszerre mérni. Tehát továbbra is egy bitnyi információnál maradunk virtuális fotononként.

Ezenkívül a részecskék nem hordozzák azt a szuperszámítógépet, amely csaknem végtelen számú méretű bozon adatainak feldolgozásához szükséges. Nincs ismert fizikai mechanizmus arra, hogy az egyes adatbiteket összegyűjtsék és értelmes utasításokká rendezzék.

Továbbá, mivel egy virtuális foton egy foton fél hullámhosszának felel meg, ahhoz, hogy a részecskék virtuális fotont cseréljenek, a virtuális foton energiája kizárólag a részecskék közötti távolságtól függ. Tehát az egyetlen adat, amelyet egy virtuális foton továbbíthat, az a virtuális foton hullámhossza, amely egyenlő a távolsággal.

Aztán egy foton kibocsátásához és elnyeléséhez nem lehet virtuális foton, mivel nem áll rendelkezésre fizikai mechanizmus arra, hogy egy részecske kibocsásson vagy elnyeljen egy virtuális fotont.

De ha egy mérőbozon egy nem virtuális foton, akkor a kibocsátó részecske energiát veszít, a fogadó részecske pedig energiát nyer, ami nincs összhangban a megfigyeléssel. És még egyszer, a szabványos modellben nincs fizikai mechanizmus arra, hogy egy részecske ténylegesen fotont hozzon létre.

Szintén fontos, hogy a részecskéknek nincs meghajtórendszerük, így nem tudnak megfelelően mozogni, ha a bozonok megmondják, hogyan mozogjanak.

A legnyilvánvalóbb, hogy a fotonok és a virtuális fotonok valójában nem részecskék, amint azt a 4. és 5. hazugság tárgyalja. Mivel a fotonok eleve nem alapvető részecskék, nem alkalmasak arra, hogy mérőbozonok legyenek. Az éter tényleges vákuum-ingadozásait sokkal jobban jelölhetjük erőhordozó közegként.

Ez a hazugság bizonyos értelemben helytálló volt, mert néha azt állítják, hogy az elektromos és mágneses terek fotonokból állnak. A hiba az volt, hogy nem fotonok, hanem vákuumfluktuációs dipólusok alkotják az elektromos és mágneses teret. Ha egyszer már léteznek virtuális töltési dipólusok az egész térben, az elektromágneses térelmélet hirtelen értelmet nyer.

8. hazugság: Az elektromágneses mezők nem valósak

Úgy gondolom, hogy minden fizikus hajlamos arra a nézetre, hogy az egyik részecske által a másikra kifejtett összes erőt, minden molekuláris hatást és magát a gravitációt valamilyen módon az éter adja át, ahogy ez a megfeszített kötél feszültségében és a vasrúd rugalmasságában is megnyilvánul, tehát meg kell találni a magyarázatot arra, hogy mi történik az éterben a molekulák között. Ezért, mivel aligha vallhatjuk be, hogy egy és ugyanaz a közeg képes két vagy több cselekvést teljesen különböző mechanizmusokkal közvetíteni, minden erőt többé-kevésbé szorosan összefüggőnek tekinthetünk azokkal, amelyeket az elektromágnesességben vizsgálunk. 18

Hendrick Lorentz, 1906

A 8. nagy fizika hazugság, hogy az elektromágneses mezők nem valósak. Michael Faraday az 1800-as évek elején fedezte fel az elektromos és mágneses tereket. Mezői kényelmes módjai voltak annak leírására, hogyan terjednek az elektromos és mágneses kölcsönhatások a térben. Ezek a mezők a számítások alapjául szolgáltak, és szerepelnek az elektromosság és a mágnesesség alapvető egyenleteiben.

Faraday korában senki sem tudta, mik ezek a mezők, vagy mi hozta létre őket. Volt egy olyan elképzelés, hogy van valami az éterben. Amikor Maxwell az elektromos és a mágneses egyenleteket egy összefüggő elektromágneses elméletté egyesítette, amely a nevét viseli, a mezőket örvényekként jelenítette meg. Úgy gondolta, hogy a vezetéken átfolyó áram örvényt idéz elő, és fordítva, az éterben forgó örvény áramot okozhat a vezetékben. Valahogy lehetségesnek tartotta, hogy az örvények elektromos mezőkké egyesüljenek. Ez a modell elég jól működött a mágneses mezőknél, de nem olyan jól az elektromos mezőknél, és bár fontos volt felfedezései számára, elméletének ennek a részét már régen elvetették.

Amikor a Michelson-Morley-kísérlet megtörtént, és az éterelmélet megkérdőjeleződött, még mindig volt bizonyos elképzelés, hogy a mezők valamilyen módon terjednek az éteren keresztül. Ezen a ponton az éterelutasítók elakadtak. Ha nem lenne éter, akkor a mezők fizikailag nem lennének valódiak. Ennek ellenére a térelmélet jó modellt nyújtott az erők működésének megjelenítéséhez, és az egyenletek továbbra is a térerősségeken alapultak.

Több mint egy évszázada tanítják a fiatal fizikusokat a mezőkről, azok szemléltetéséről és kiszámításáról. Aztán azt mondják nekik, hogy az elektromágneses mezők nem valósak. A térben semmi sem magyarázza meg őket, így a mezők csupán vizuális és matematikai modellezési technikák.

Ez a probléma. Ha a mezők nem valósak, akkor nincs mód az elektromágneses erőknek a térben való terjedésére. Nélkülük nincs közvetítő közeg az erőknek a részecskék és az anyagtestek között. Ráadásul nincs olyan hatásmechanizmus, amely a részecskéket és az anyagtesteket mozgatná. A fizikusoknak megmaradtak a mágikus távoli cselekvések és a mágikus mozgáselméletek, amelyek ma is velünk vannak.

Voltak fizikusok, akik felismerték, hogy léteznek vákuum-ingadozások, de tévedésből fotonként modellezték őket. Aztán az volt az elképzelésük, hogy a fotonok együttesének valami köze van az elektromágneses térhez, ami különbözik a mérőbozonmodelltől. Egyesek odáig mentek, hogy azt mondták, hogy ez a fotonmező polarizálható, de mégsem tudták, hogy a mező dipólusokból áll, amelyek minden bizonnyal polarizálhatók.

Most már tudjuk, ahogy Casimir megjósolta, hogy az éter tele van elektromos dipólusokkal. Ezeknek a dipólusoknak az egyik végén pozitív, a másikon negatív töltésük van. Casimir elmélete alapján azt is tudjuk, hogy ezek a dipólusok a van der Waals-erőknek megfelelő módon kölcsönhatásba lépnek. Az éter-dipólusok más éter-dipólusok mozgásától függően mozognak, és rányomhatják az anyagtesteket, amint azt kísérletileg bebizonyították.

Ez elvezet bennünket a diszkrét Faraday-erővonalak képéhez, amelyek mindegyikéhez egy -e vagy +e töltet kapcsolódik. Minden vonalhoz tartozik egy irány, így a két végű vonal végei nem azonosak, és az egyik végén +e, a másik végén pedig –e töltés van. 19

Paul Dirac, 1963

Ha az éter-dipólusok más dipólusok mozgása miatt mozognak, akkor az elektromos töltések miatt is mozoghatnak, függetlenül attól, hogy ezek a töltések állók vagy mozgóak. Az éter-dipólokat elektromos töltés polarizálja. Az éter-dipólusok elektromos töltés vagy áram mozgása miatt forognak.

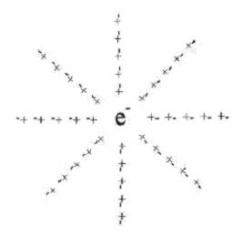
8-1. ábra Egy szabad elektron, amelyet éter-dipólusok vesznek körül, amelyek az elektromos töltése hatására polarizálódnak.

Az elektromos és mágneses mezők valóságosak. Az étert kitöltő vákuumfluktuációs dipólusokból állnak. Az elektromos mezők polarizált éterek. A mágneses mezők az éter forgását jelentik. Az elektromágneses terek, legyenek azok polarizációk vagy forgások, pontról pontra dipólusról dipólusra terjednek az éterben.

Azok a tanítások, hogy az elektromágneses mezők nem valósak, hazugságok. Az elektromágneses tér elmélete nem elvont fogalom; fizikailag valóságos. A mezőket nem varázslat hozza létre. A vákuum dipólusai valóban léteznek.

18 H. A. Lorentz, Theory of Electrons, 2. kiadás, B. G. Teubner, Lipcse, G. E. Stechert & Co., New York, 1916, 45. o. (1906-ban elhangzott előadássorozatból.)

19:00 Dirac, „A fizikus természetképének fejlődése”, Scientific American, 1963. május, 208(5), 45-53.

9. hazugság: Az elektromágneses elmélet megmagyarázza a mozgást

A fizikában a 9. legnagyobb hazugság, hogy az elektromágneses elmélet megmagyarázza a mozgást. Werner Heisenberg és azóta a fizikusok többsége lezártnak, teljes elméletnek tekinti az elektromágneses elméletet. 20 Sajnos soha nem jutottak el ahhoz, hogy leírják, hogyan mozognak a testek az elektromos és mágneses erők hatására. Soha nem találtak ki fizikai modellt a mezőkre sem. Elhanyagolták azt a kérdést, hogy mit jelent a taszítás és hogyan jön létre ez a taszítás? Vagy ha megkérdezték tőlük, gyorsan elhallgatták őket, és azt mondták: ne aggódjanak az ilyen dolgok miatt. A mai mainstream fizikusok továbbra is úgy tesznek, mintha elméletük megmagyarázná a mozgást, holott nem.

Hogy ez hogyan történt, az az egész fizikában konzisztens probléma. Először is: a matematikusok átvették a fizikát. Fogd be szád, és számolj, ez a mantrájuk. Úgy tűnik, nem is törődnek az alapvető fizikai jelenségek, az alapvető fizika megértésével. Mindaddig, amíg el tudnak végezni egy olyan számítást, amely lehetővé teszi számukra, hogy megjósoljanak bizonyos eredményeket, boldogok.

A probléma második része a vákuum-ingadozás figyelmen kívül hagyóiban rejlik, akik a fizikát irányítják. Amikor két test között az egyetlen dolog a vákuum, és tagadják bárminek is a vákuumban való létezését, akkor csak annyit tehetnek, hogy feladják a mögöttes mechanizmusok megértését. Ezután folyamatosan hazudniuk kell a nyilvánosságnak, és be kell tanítaniuk a tanítványaikat a hamis dogmáikba, vagyis úgy kell viselkedniük, mintha valahogy megértették volna a jelenséget. Ám az őszinteség pillanataiban olykor megengedhetik maguknak, hogy beismerjék: ez meghaladja a megértésüket, mégis úgy tesznek, mintha az örök tudatlanságukkal minden rendben lenne.

Szerencsére nem kell a tudatlanságban maradnunk, hiszen léteznek vákuum-ingadozások, amelyek tökéletes közeget alkotnak a testek közötti erőátvitelhez, és mint kiderült, mozgást is előidéznek.

Szerencsések vagyunk abban is, hogy Hendrik Casimir, a múlt század egyik legbriliánsabb fizikusa felfedezte az erők működésének alapjait a vákuummal kapcsolatban. Rájött, hogy a vákuum-ingadozások töltésdipólusok, amelyek kölcsönhatásba lépve van der Waals-erőket hoznak létre, és eltaszítják az anyagi testeket.

Azt is felismerte, hogy a van der Waals-erők nyomást hoznak létre a tárgyakon, és ez a nyomás megváltozik, ha bizonyos vákuum-ingadozásokat kizárunk a tér egy régiójából. Amint azt korábban említettük, legalapvetőbb példájában a kizárási zóna két lemez közötti tér, és ezeket a lemezeket egymáshoz tolják, amikor elég közel vannak ahhoz, hogy kizárják a jelentős vákuum-ingadozási hullámhosszokat. A lemezeket összenyomó külső nyomás ekkor meghaladja a lemezeket szétnyomó belső nyomást.

A vákuum-ingadozást elutasítók túlságosan elfoglaltak voltak azzal, hogy figyelmen kívül hagyják Casimir munkáját az elmúlt 70 évben ahhoz, hogy rájöjjenek, hogy erőmechanikája minden elektromágneses erőre kiterjeszthető. A Van der Waals-erők, kibővítve a Casimir-erőkkel, végül is az elektromágneses erőelmélet részét képezik.

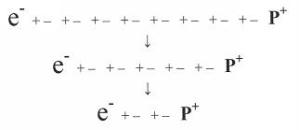
9-1. ábra Egy szabad elektron és proton összenyomódik, mivel a nyomás csökken közöttük.

Például két ellentétes töltésű test polarizálja a köztük lévő vákuum-ingadozásokat. A virtuális dipólusok pozitív töltései más dipólusok negatív töltéseire utalnak, amint az a fenti ábrán látható. Amikor egy dipólus megsemmisül, a mellette lévő dipólusok közelebb kerülnek egymáshoz. Ez a van der Waals nyomás csökkenéséhez vezet az ellentétes töltések között, ami lehetővé teszi, hogy a külső van der Waals erők összenyomják őket.

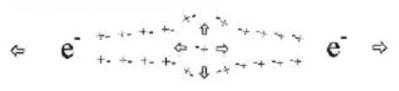
9-2. ábra Két szabad elektron, köztük polarizált dipólusokkal, amelyek azt mutatják, hogyan növekszik a nyomás az elektronok széttolása között.

Másrészt, amikor két hasonló töltés van, a vákuum-dipólusok a középső pontban egymással szemben állnak, ami a töltések közötti van der Walls nyomás növekedéséhez vezet, ami a testeket széttolja. A kifelé irányuló nyomás legyőzi azt a nyomást, amely összenyomja őket.

A legtöbb ember már játszott a mágnesekkel, és jól ismeri azt a jelenséget, hogy ha két mágnes északi pólusait megpróbálja összeilleszteni, akkor azok ellökődnek egymástól. És ha nem irányítja őket, az egyik gyorsan körbe fog forogni, így a két mágnes északi és déli pólusa egymáshoz tapad.

A legtöbb ember nem veszi észre, hogy a mágnesek között kevés a vákuum fluktuációs dipólus. Ezek a dipólusok úgy forognak, hogy kis mágnesekké válnak. Ezek a kis virtuális mágnesek azután úgy igazodnak a fizikai mágneshez, hogy déli pólusuk a fizikai mágnes északi pólusa közelében legyen.

Ily módon egy csomó kis virtuális mágnes sorakozik a két fizikai mágnes között, és csakúgy, mint a töltéseknél, ha az összes virtuális mágnes az északi pólustól a déli pólusig sorakozik, akkor a mágnesek közötti nyomás csökken, és így a mágneseket a külső van der Waals erők tolják össze.

Aztán ha két fizikai mágnes sorakozik az északi pólusaikkal együtt, akkor egyes virtuális mágnesek északi pólusai együtt vannak, amitől eltérnek egymástól, és így megnő a taszítás a két mágnes között. A mágneseket széttoló nyomás ekkor nagyobb, mint az összenyomó nyomás, és a mágnesek szétrepülnek. Ugyanez történik, ha két mágnes a déli pólusait nyomja össze.

A mainstream fizikusok minden bizonnyal hazudnak, amikor azt állítják, hogy elméletük az elektromágneses mozgást megmagyarázza. De az egyszerű magyarázat évtizedek óta előttük van: az elektromágneses mozgás a kiterjesztett Casimir-effektusnak köszönhető, és az éter létezésének tagadása felelős a tudósok kudarcáért.

Az az állítás tehát, hogy az elektromágneses elmélet megmagyarázza a mozgást, hazugság. Ha megértjük a vákuum-ingadozásokat és Casimir elméletét, nyilvánvaló, hogy minden elektromágneses mozgás a nullponti mező nyomáskülönbségeinek, a kiterjesztett Kázmér-erőnek köszönhető.

20 A. Bokulich: „Nyitva vagy zárva? Dirac, Heisenberg, and the Relation between Classical and Quantum Mechanics, Studies in History and Philosophy of Modern Physics 35(3) (2004)

10. hazugság: Mágneses monopólusok

A 10. nagy fizika hazugság a mágneses monopólusok. A legtöbb ember tudja, hogy minden mágnesnek van északi és déli pólusa. Még ha egy mágnest kettévágnak is, mindkét darabnak van északi és déli pólusa. A mágneses monopólus gondolata az, hogy valamiképpen létezhetne egy északi pólus déli pólus nélkül, és egy déli pólus létezhetne északi pólus nélkül.

Egyes fizikusok azt akarják hinni, hogy a mágnesesség elektrosztatikus erőkként írható le. Az elektrosztatikus erőknek külön pozitív és negatív töltésük van, ezért matematikailag kényelmes lenne, ha az északi és a déli mágneses pólust két különálló mágneses töltésként lehetne kezelni. Ez nem más, mint vágyálom, és nincs alapja a fizikai valóságban, de továbbra is előkerül.

Ez egy másik probléma, amely a vákuum-ingadozások tagadásán alapul. Különösen, ha valaki felismeri a Casimir-effektus létezését, a vákuum tele van dipólusokkal. Ezek a dipólusok forogva mágneses mezőket és sok kis mágnest képeznek. A forgó dipólusoknak mindig van északi és déli pólusa is, tehát minden létező mágneses térnek rendelkeznie kell északi és déli pólussal is.

Még a legalapvetőbb mágneses mezőnek, az elektron mágneses mezőjének is van északi és déli pólusa. A részecskék mágneses pólusai nem léteznek, és nem is létezhetnek egymástól függetlenül.

Az univerzum ősrobbanás-modelljének állítólag monopólusproblémája is van, mivel egyes fizikusok elképzelései arról, hogyan keletkezett az anyag közvetlenül az ősrobbanás után, számos monopólus kialakulását is magában foglalja. Mivel a mágneses monopólusok kísérletileg nem léteznek, és nem létezhetnek dipólusokkal teli nullponti mezőben, ez nagy probléma. Ez azt mondja nekünk, hogy a fizikusok mágneses monopólusokat igénylő anyag előállítására vonatkozó képletei hazugságok.

A mágneses monopólusok hazugság. Nem létezhetnek. Minden elmélet, amely hipotetikus mágneses monopólusokat tartalmaz, szintén hazugság. Igazság szerint a mágneses monopólusok egyértelműen a sci-fi kategóriába tartoznak.

11. hazugság: A fénysebesség minden vonatkoztatási rendszerben állandó

A 11. nagy fizika hazugság az, hogy a fénysebesség minden vonatkoztatási rendszerben állandó. Természetesen hozzá kell tennünk a „vákuumban” figyelmeztetést. A fénysebesség állandósága egy másik probléma, amely a vákuum-ingadozást elutasítóknál mindig előjön. És végül más problémákat, más hazugságokat okoz, különösen annak megértésében, hogy a különböző sebességgel mozgó megfigyelők hogyan látják a fényt egy adott forrásból. Más szavakkal, problémákat okoz a relativitáselmélet számára.

Maxwell volt az, aki először értette meg a fényelméletet. Felismerte, hogy a fény elektromágneses, és illeszkednie kellett az általa összeállított elektromágneses egyenletgyűjteményhez. Azt is felismerte, hogy a fény az éter közegén halad keresztül, a világító éteren, ahogyan nevezték. Ezenkívül rájött, hogy az éternek nyugalmi állapottal kell rendelkeznie, olyan vonatkoztatási rendszerrel, ahol az éter nyugalomban van, vagy általánosabban a mozgásátlaga nulla. Nyugalmi állapotban az éter minden irányban homogénnek tűnik, a fénysebesség pedig minden irányban állandó.

A legfontosabb, hogy ezzel a témával kapcsolatban Maxwell felismerte, hogy a fény az éter nyugalmi állapotában éri el maximális sebességét. 21 Következésképpen úgy tűnik, hogy a fény lassabb sebességgel rendelkezik bármely vonatkoztatási rendszerben, amely az éter nyugalmi állapotához képest mozog. Erre a következtetésre az éter fényáramról alkotott hipotézise miatt jutott el, amely a Michelson-Morley-kísérlethez vezetett. Míg a vontatási hipotézise téves volt, nem tévedett a mozgó vonatkoztatási rendszerek fénysebességét illetően.

A Michelson-Morley-kísérlet után az éter-elutasítók vették át az uralmat, és Maxwell fénysebesség-elmélete megkérdőjeleződött. Maxwell elmélete szerint a fénysebesség a világító éter tulajdonsága volt a fényfotonokkal való kölcsönhatás szempontjából. De ha nincs éter, hogyan határozható meg a fénysebesség? Az éter elutasítói az egyetlen következtetésre jutottak, amire képesek voltak: a fénysebességnek a fény belső tulajdonságának kellett lennie. A fény egyszerűen tudja, mekkora sebességgel kell rendelkeznie. Természetesen ez az elképzelés, hogy a fénysebesség a fény belső tulajdonsága, hazugság.

Mivel tudjuk, hogy az éter igenis létezik, és minden esetben egy világító éter, vissza kell térnünk Maxwell hipotéziséhez, miszerint a fénysebesség a fotonok és terjedési közegük közötti kölcsönhatásnak, a vákuum fluktuációjának köszönhető. Ezután meg kell értenünk a Michelson-Morley kísérlet eredményét ebben az összefüggésben. Négy fontos szempontot kell figyelembe venni.

1. A Michelson-Morley kísérlet azt mutatta, hogy egy adott vonatkoztatási rendszerben a fény kétirányú sebessége független az iránytól. Megjegyzendő, hogy a kétirányú kifejezést a pontosság kedvéért használjuk, mivel a kísérlet nem kísérli meg az egyirányú sebesség mérését, amihez óraszinkronizálás szükséges.

2. A fénysebesség bármely referenciakeretben mérve azonos, függetlenül az éter nyugalmi kerethez viszonyított sebességétől. A sebesség körülbelül 3 x 108 méter másodpercenként. Jegyezze meg itt, hogy két mértékegység van, egy a távolságra és egy az időre, mivel ez fontos.

3. Egy monokromatikus fényforrás iránytól függetlenül ugyanazt az energiát bocsátja ki egy adott referenciakeretben. Ugyanakkor a monokromatikus fénynek más energiája lesz, ha a forráshoz képest mozgó detektorral mérik. Tehát a detektor fényforráshoz viszonyított sebessége befolyásolja a mért fotonenergiát.

A fenti bizonyítékok alapján két lehetséges következtetés vonható le a fénysebességre vonatkozóan.

A. A fény sebessége minden referenciakeretben állandó, és az éter nyugalmi állapotához/keretéhez viszonyított sebessége nem változtatja meg a fény sebességét.

B. A fénysebesség nem állandó minden referenciakeretben, de az órajel egy mozgó referenciakeretben úgy változik, hogy a fénysebesség egy mozgó vonatkoztatási rendszerben azonosnak tűnik.

Figyelembe kell vennünk a relativisztikus hatásokat a mozgó vonatkoztatási keretekre, hogy kitaláljuk, melyik a helyes a fenti két választás közül. A mozgó referenciakeretben az órajel lassabb, mint az éter nyugalmi keretben, amint azt kísérletileg bebizonyították. Az órajel lassításának alapegyenlete a 11-1 egyenlet, ahol t' az időintervallum a mozgó vonatkoztatási rendszerben, t 0 az időintervallum az éter nyugalmi keretben, v a referenciarendszer sebessége az éter nyugalmi keret és c a fénysebesség.

11-1 egyenlet

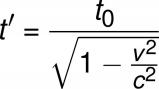
Az éter nyugalmi állapotához képest mozgó vonatkoztatási rendszerben megtett távolság kisebb, mint az éter nyugalmi állapotában a 11-2 egyenletben megtett távolság alapegyenlete szerint, ahol x' a mozgó vonatkoztatási rendszerben megtett távolság és x0 az éter nyugalmi állapotában megtett távolság. Vegye figyelembe, hogy a nevezőben szereplő tag mindkét egyenletben ugyanaz. Az idő és a távolság azonos ütemben változik.

11-2 egyenlet

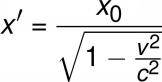
Következésképpen a fénysebesség lassabb az éter nyugalmi keretéhez képest mozgó vonatkoztatási rendszerben, de nem veszik észre, mert az órajel ugyanilyen mértékben lassabb. Bármely mozgó referenciakeretben mért fénysebesség megegyezik valaki által abban a vonatkoztatási keretben mért sebességgel, még akkor is, ha a fénysebesség nem állandó, ha az éter nyugalmi keretben lévő órával mérjük.

Ez újabb választ ad arra a kérdésre, hogy a fény sebessége hogyan független az iránytól. Részben azért, mert az éter nyugalmi állapotának órajele független az iránytól.

Tehát Maxwellnek igaza volt abban, hogy a fénysebesség az éter nyugalmi állapotában a leggyorsabb, és lassabb bármely más vonatkoztatási rendszerben, legalábbis az éter nyugalmi állapotában lévő megfigyelő által mérve. Tévedett, amikor azt gondolta, hogy az éter-ellenállásnak van irányfüggősége, mivel a fény mindig az éter nyugalmi állapotában halad. Mind a fotonenergia, mind a sebesség független attól, hogy a foton milyen irányt bocsát ki a forrásból.

Az az állítás, hogy a fénysebesség minden referenciakeretben állandó, hazugság. A fénysebesség csak azért tűnik állandónak, mert az órajelek egyenlő mértékben változnak, hogy így tűnjön.

A fény sebessége vákuumban csak az éter nyugalmi állapotában állandó, ahol a foton ténylegesen halad, függetlenül a forrás vagy a detektor mozgásától. Tehát valóban állandó, de nem minden referenciakeretben, ahogyan azt mondják, de ez a következő.

21 J. C. Maxwell, „On a Possible Mode of the Detecting a Motion of the Solar System Through the Luminiferous Ether”, Nature, 1880, Vol. XXI, 314., 315. o.

12. hazugság: A Fénysebesség minden megfigyelő számára állandó

A fizikában a 12. legnagyobb hazugság az, hogy a fénysebesség minden megfigyelő számára állandó. Még egyszer hozzáadjuk a figyelmeztetést vákuumban. Ez a hazugság közvetlenül következik a 11. hazugságból, miszerint a fénysebesség minden referenciakeretben állandó. Mint a fizika legtöbb hazugsága, ez is a vákuum-ingadozások, a modern éter létezésének tagadásának köszönhető. A fotonok átviteli közege nélkül a fénysebességnek a foton alapvető tulajdonságának kellett lennie.

A speciális relativitáselmélet megfogalmazásakor Einstein abból a feltételezésből indult ki, hogy a fotonoknak azonos sebességgel kell rendelkezniük minden megfigyelő számára, függetlenül attól, hogy mekkora sebességük van egymáshoz képest. 22 Abban az időben nem hitt az éterben, ezért nem vette figyelembe az éter nyugalmi állapotát a gondolkodásában; valójában eltávolította az étert mások elméleteiből, hogy kidolgozza saját speciális elméletét. Einstein állítólag átélt néhány olyan időszakot életében, amikor úgy gondolta, hogy a vákuum-ingadozások és az éter valós lehet, 23 de többnyire elutasította az éter létezését, és elméletei ezt a nézőpontot tükrözik vissza.

Ezen a ponton fontos figyelembe venni a kétirányú fénysebességet az egyirányú fénysebességgel szemben, mivel egyesek úgy gondolják, hogy ezzel is bizonyítani tudják az éter létezését. Úgy gondolják, hogy a fény egyirányú sebessége az éterhez viszonyított irányától függően eltérő lehet. Ez ismét egy éterellenállás-hipotézisen alapul.

Mivel a fény az éter nyugalmi állapotában halad, nem pedig egy mozgó forrás referenciakeretében, ez a teszt érvénytelen. A fény bármely irányban azonos sebességgel halad egy adott nyugalmi állapotban. Következésképpen minden olyan kísérlet, amely megmutatná, hogy a fény egyirányú sebessége két irányban azonos, nem cáfolná az éter létezését.

A tudósok nem tudják közvetlenül megmérni a csillagokból vagy galaxisokból érkező fény sebességét. Az egyirányú fénysebesség sem mérhető közvetlenül anélkül, hogy előzetesen ne feltételeznénk az órák szinkronizálását és a relativisztikus órajel-változásokat. Kísérletileg nem tudhatjuk, hogy az egyirányú fénysebesség minden megfigyelő számára állandó-e.

Ha egyetlen forrásból származó fotonáramot vesszünk, akkor hipotetikusan csaknem végtelen számú megfigyelő figyelheti meg őket, akik közel végtelen számú különböző relatív sebességgel haladnak. Minden megfigyelő azt mondja, hogy a fotonok a szokásos fénysebességgel haladnak

. Ez felveti a kérdést, hogyan tud egy foton egyszerre csaknem végtelen számú relatív sebességgel mozogni? Ez a kérdés természetesen lenyűgözi a fizikusokat, és úgy tűnik, hogy inkább elbűvölte őket, hogy ezt elfogadják, mintsem hogy elutasítsák, mert irracionálisnak hangzik. A racionálisabb nézet az lenne, ha a relativitáselméletre hagyatkoznánk, és azt mondanánk, hogy a fény csak úgy tűnik, hogy ugyanazt a sebességgel mozog, mert a távolságmérés és az órajel minden mozgó vonatkoztatási rendszerben eltérő. A fény természetesen mindig a nyugalmi állapotában utazik.

A vákuum-ingadozás visszautasítói természetesen helytelenül vélekedtek. Létezik a vákuum-ingadozás és az éter. Az éter a fotonok átviteli közege. Még ennél is fontosabb, hogy a fotonok teljes egészében vákuum-ingadozásokból állnak, így ahhoz, hogy a fotonok relatív sebessége végtelenül változzon, az éter összes vákuum-ingadozásának válaszul végtelen számú foton-dipólus szögsebességgel kell forognia. Valójában végtelen számú éternyugalmi állapotra lenne szükségünk. Ez azonban lehetetlen és teljesen irracionális. Ehelyett az éternek egyetlen nyugalmi állapota van, amint azt a kozmikus mikrohullámú háttérsugárzás mérései kísérletileg igazolták, és az összes fényt ebben a nyugalmi állapotban továbbítják.

Ahogy Maxwell az 1800-as évek közepén arra a következtetésre jutott, hogy a maximális fénysebesség csak az éter nyugalmi állapotában érhető el. Bármely más vonatkoztatási rendszerben a fénysebesség lassabb, ha az éter nyugalmi állapotban lévő órával mérjük, de a mozgó megfigyelő számára a mozgó megfigyelő órájának relativisztikus óralassulása miatt ugyanannak tűnik.

Mint korábban megjegyeztük, mivel a fény ugyanazokból a vákuum-ingadozásokból áll, amelyek az étert alkotják, és a fény áthalad az éteren, helyénvaló az éter nyugalmi állapotában haladó összes fotonra gondolni. Így, ha ténylegesen megpróbáljuk kiszámítani az energia, a távolság vagy az órajel változásait, az éter nyugalmi állapotot használhatjuk szabványos referenciakeretként minden konverzióhoz. Annak ellenére, hogy az uralkodó téves elméletnek nincs szabványos vonatkoztatási kerete, mégis hozzá kell rendelnünk egyet a számítások elvégzéséhez. Számunkra jobb, ha létezik egy szabványos referenciakeret. Ezzel el lehet kerülni, hogy számos paradoxon felbukkanjon.

Az a feltételezés, hogy a fénysebesség minden megfigyelő számára azonos, hazugság. Ez a hazugság az éter elutasítása és a fotonok világító éteren áthaladó rossz feltételezése miatt jött létre.

22 A. Einstein, "Zur Elektrodynamik bewegter Körper", Annalen der Physik 322 (10): 891–921, 1905.

23 A. Einstein, „Æther és a relativitáselmélet”, 1920. május 5-én elhangzott beszéd a Leydeni Egyetemen, Németországban.

13. hazugság: Speciális relativitáselmélet

A fizika legnagyobb hazugságai közül a 13. a speciális relativitáselmélet. Ez nem jelenti azt, hogy minden korábbi relativitáselmélet hazugság, mivel láttuk, hogy ez szükséges az idő, a távolság és az energia megértéséhez a mozgó vonatkoztatási keretekben lévő megfigyelők szemszögéből. A probléma az, hogy Einstein sajátos feltételezést tett a speciális relativitáselmélet kidolgozásakor, ami megkülönböztette elméletét a korábbi relativitáselméletektől. Einstein feltételezte, hogy éter nem létezik. Tehát ez egy újabb eset, amikor egy éter-tagadó érvénytelen elmélettel áll elő.

Míg a népszerűsített tudományban általában azt mondják, hogy Einstein a relativitáselmélet feltalálója, a kifejezést Poincaré francia fizikus alkotta meg. Sok tudós jelentős előrelépést tett a relativitáselmélet terén Einstein előtt, mint például Fitzgerald, Lorentz, Larmor és természetesen Poincaré. 24-31 A relativitáselmélet korai kidolgozói feltételezték, hogy létezik éter, és lépéseket tettek annak érdekében, hogy az étert beépítsék a relativitáselméletbe.

Einstein nem volt hajlandó felismerni, hogy éter létezik, és ami ugyanilyen fontos: nem volt hajlandó elismerni, hogy létezik éter-nyugalmi állapot, és hogy az éter-nyugalmi állapot a relativitáselmélet standard vonatkoztatási kerete. Ez ahhoz a problémához vezetett, hogy egy adott probléma megoldása során bármilyen vonatkoztatási rendszer választható standard referenciakeretként. De attól függően, hogy melyik referenciakeretet választottuk, eltérő eredmények születnek. Az az elképzelés, hogy relativisztikus állapot-transzformációkat végre lehet hajtani szabványos referenciakeret nélkül, hazugság.

Ezek az eltérő eredmények a speciális relativitáselmélet úgynevezett paradoxonjaihoz vezettek, köztük a híres ikerparadoxonhoz. A speciális relativitáselmélet paradox természete figyelmeztetés kellett volna, hogy legyen: minden olyan elmélet, amely feloldhatatlan paradoxonokat vezet be, hazugság!

A fizikusok azt mondják, hogy egy szabványos vonatkoztatási rendszer kiválasztásával feloldották az iker-paradoxont, de ez nem oldja meg a mögöttes alapvető paradoxont. A speciális relativitáselmélet szerint, amikor egy ikerpár közel fénysebességgel távolodik egymástól, nem tudhatjuk, melyik ikertestvér öregszik. A Lorentz-relativitáselméletben megmérjük a sebességüket az éter nyugalmi keretéhez képest, és akkor tudjuk, hogy melyik öregszik gyorsabban, és melyik a lassabb órajel.

A vákuum-ingadozások igazolt létezésének fényében Einstein feltételezései bizonyítottan tévesek. Íme egy lista a legnagyobb hibáiról, amelyeket speciális relativitáselméletének kidolgozása során követett el:

1. Einstein tévesen feltételezte, hogy nincs éter

2. Einstein tévesen feltételezte, hogy nincs szabványos nyugalmi állapot

3. Einstein tévesen feltételezte, hogy a fénysebesség a foton sajátossága

4. Einstein tévesen feltételezte, hogy a szabványosított nyugalmi állapot szükségtelen

5. Einstein tévesen feltételezte, hogy a fénysebesség minden vonatkoztatási rendszerben állandó.

6. Einstein tévesen feltételezte, hogy a fény a fényforrásának vonatkoztatási rendszerében halad.

7. Einstein tévesen feltételezte, hogy a fénysebesség minden megfigyelő számára állandó. Einstein rosszul választott. Mindezen téves feltételezések egyik következménye, hogy számos hiba bukkan fel, amikor valaki megpróbálja alkalmazni a speciális relativitáselméletet. Végül a fizikusoknak valójában az egyenletek Lorentz-Poincaré változatát kell használniuk, gyakran frissített formában, és gondosan ki kell választaniuk egy szabványos vonatkoztatási rendszert a transzformációk végrehajtása során.

Most, hogy a Planck-típusú éter létezését kísérletileg bebizonyították, minden relativitáselmélet alapismeretével rendelkező fizikus tudja, hogy Einstein tévedett, és a speciális relativitáselmélet hazugság. Egyes fizikusok azt mondják, hogy a speciális relativitáselmélet nincs összhangban a kvantumtérelmélettel, amely csak egy másik neve az éterelméletnek, de nem teszik meg azt a fontos és szükséges lépést, hogy hiteltelenítsék a speciális relativitáselméletet. Vegyük észre, hogy a Lorentz-Poincaré relativitáselméletben is vannak hazugságok, amint azt hamarosan látni fogjuk.

24 G.F. FitzGerald, "Az éter és a Föld légköre", Science 13 (328): 390, 1889.

25 H.A. Lorentz, "A Föld és az éter relatív mozgása", Zittingsverlag Akad. V. Nedves. 1: 74–79, 1892.

26 J. Larmor, "Az elektromos és fényes közeg dinamikus elméletéről, 3. rész, Kapcsolatok anyagi médiával", Phil. Trans. Roy. Soc. 190: 205–300, 1897.

27 J. Larmor, Aether and Matter, Cambridge University Press, 1900.

28 W. Voigt, "On the Principle of Doppler", Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen (2): 41–51, 1887.

29 H. Lorentz, "Simplified Theory of Electrical and Optical Phenomena in Moving Systems", Proceedings of the Royal Netherlands Academy of Arts and Sciences 1: 427–442, 1899.

30 H. Lorentz, "Electromagnetic phenomena in a system moving with any velocity smaller than that of light", Proceedings of the Royal Netherlands Academy of Arts and Sciences 6: 809–831, 1904.

31 H. Poincaré Bull. Sci. Math, (2) 28, 317-, November 1904. English translation: Bull. Amer. Math. Soc. 37, 2000, 25 –

14. hazugság: Hossz-összehúzódás

A fizikában a 14. legnagyobb hazugság a hossz-összehúzódás. A hossz-összehúzódás azt jelenti, hogy a fizikai rudak és más tárgyak rövidebbek lesznek, amikor az éter nyugalmi keretéhez képest mozognak. Ez a jelenség a relativitáselmélethez kapcsolódik, ahol az egyik referenciakeretben lévő megfigyelő egy másik referenciakeretben lévő objektumot figyel meg, és amikor az objektum a fénysebességhez közeli sebességgel mozog, akkor a megtett távolság lerövidülését látja. Bár a megtett távolság ilyen rövidülése előfordul, az eredményt gyakran félreértelmezik hossz-összehúzódásként, vagy ami még problematikusabb: rúd- vagy tárgy-összehúzódásként.

A fizikusoknak meg kellett volna kérdőjelezniük a fénysebesség irányfüggésének kezdeti feltevését, ehelyett megpróbálták kitalálni a probléma megoldásának alternatív módját. George Fitzgerald 1889-ben javasolta a hossz-összehúzódás megoldását, Hendrik Lorentz pedig néhány évvel később (1892-ben) önállóan állt elő ugyanezzel az ötlettel, de sikeresebben népszerűsítette. 24,25 Ma Lorentz-Fitzgerald hosszúságú kontrakcióként ismert.

Megoldásuk az volt, hogy a távolságok fizikailag rövidebbek lettek az éter nyugalmi keretéhez viszonyított iránytól függően. A Michelson-Morley-kísérlettel szemben, bár az úthosszakat ott azonosnak mérték, a hossz-összehúzódás elmélete azt mondta, hogy valójában különböznek.

Ezzel sikerült megmenteni az irányfüggőség eredeti feltevését és megoldani a problémát. Azonban új problémát jelentett, hogy hogyan lehet a hosszúságokat azonosra mérni, de amint a fény haladt ezen az utakon, a hosszúságok lerövidültek. Természetesen ez nem racionális megoldás.

A csillagok hullámhosszának eltolódásának Doppler-Fizeau-effektusa akkoriban jól ismert volt, és támpontot kellett volna adnia tévedésükhöz, mivel az is széles körben terjedt el, hogy a fény áthalad a világító éteren. Maxwell éterellenállás-hipotézise arra is utal, hogy a fény energiájának és hullámhosszának irányfüggőnek kell lennie. Ha Fitzgerald és Lorentz tényleg elgondolkodott volna, talán rájöttek volna, hogy a hossz-összehúzódás javítása szükségtelen, és Maxwell irányfüggőség téves feltételezésének megszüntetése megoldja a Michelson-Morely problémát. Hazugság azt állítani, hogy a Michelson-Morley kísérleti eredmények magyarázatához hossz-összehúzódási hipotézis szükséges.

Annak ellenére, hogy a Michelson-Morley-eredmény megoldásához nincs szükség hosszösszehúzásra, relativisztikus távolságmérés eltolódások fordulnak elő, amikor az objektumok mozgó referenciakeretében megtett távolságot mérjük. De ez azt jelenti, hogy a rúd hossza összehúzódik?

Mindenkinek egyet kell értenie abban, hogy egy rúd szabványos hosszúságú lesz, ha az éter nyugalmi állapotából figyelik. Ezután a rudat az éter nyugalmi állapotához viszonyítva rögzített sebességre lehet gyorsítani a rúd hosszának irányában. A hossz-összehúzódás elmélete szerint a rúd most rövidebb lesz, mint amikor egy megfigyelő az éter nyugalmi állapotából nézte. Egy megfigyelő számára, aki a rúddal együtt gyorsult, és még mindig a rúd vonatkoztatási rendszerében van, a rúd hossza soha nem változott.

Ugyanakkor a hossz-összehúzódás elmélete szerint a rúd szélessége mindkét megfigyelő számára azonos. Akárcsak Maxwell elméleténél, a hossz-összehúzódás elméletének továbbra is van egy irányfüggősége, amely viszont nem létezik.

Mivel egy hosszú fizikai rudat nem lehet a fénysebesség közelébe gyorsítani, nem volt lehetőség az elmélet közvetlen kísérleti tesztelésére. A fizikai hossz-összehúzódás nem bizonyított. Vannak olyan kísérletek, amelyekről egyesek úgy gondolják, hogy megerősítik a hossz-összehúzódást, de ezek az étert tartalmazó normál kölcsönhatásokkal magyarázhatók. Amint azt sok más esetben láttuk, az étert tagadók nehezen értik meg, hogy mi is történik fizikailag.

Azt is megfontolhatjuk, hogy mi történne egy fizikai rúddal, ha egyetlen irányba húzódna össze. Ha a rudat olyan sóból vagy ötvözetből alakították ki, amelynek kristályrácsköze ismert, ez azt jelentené, hogy a kristályrács az egyik irányba megváltozott, a másik irányba nem. Az anyagnak az egyik irányban sűrűbbnek kell lennie, mint a másikban. Ehhez a mögöttes anyagfizika megváltoztatására lenne szükség.

Egy másik dolog, amit át kell gondolni, hogy a rúd hogyan lép kölcsönhatásba az éterrel. A vákuum-ingadozások jelenléte mind a rúd körül, mind a rúd szerkezetén belül megváltoztatja-e valamilyen módon a rúd méreteit, amikor a rúd az éterhez képest mozog? Mivel a rúd töltött részecskékből áll, az éter a mozgó rúd hatására forogna, de önmagában az éter forgása nem változtatna a méreteken. Nincs kölcsönhatás a rúd és az éter között, ami megváltoztatná a rúd külső méreteit.

A hossz-összehúzódás hívei nem rendelkeznek olyan fizikai mechanizmus modelljével, amely figyelembe tudná venni a hossz-összehúzódást, függetlenül attól, hogy éter-elutasítók-e vagy sem. Mindkét esetben a hossz-összehúzódás egy másik mágikus elmélet, amelyet a tényleges fizika nem támaszt alá.

Ezen információkon túlmenően azt is figyelembe vehetjük, hogy a megfigyelt megtett távolság változása hogyan történik, így megértjük, hogy a megtett távolság hogyan viszonyul a hosszösszehúzódáshoz. Ahogy az előző fejezetekben említettük, az órajelek változnak az éter nyugalmi keretéhez képest mozgó referenciakeretben.

A mozgó órák lassabban járnak, mint az éter nyugalmi állapotában lévő órák. Ennek az az oka, hogy a távolságok rövidebbnek tűnnek a megfigyelő számára az éter nyugalmi állapotában, mert a megfigyelő órája gyorsabban jár, és nem azért, mert a távolság egységei rövidebbek lettek.

A korai relativitáselmélet kutatói két lehetséges magyarázattal álltak elő a megtett távolság változásaira, a hossz-összehúzódásra és az idődilatációra, és először rosszra megoldásra jutottak. A t’ idő nem egyenlő t-vel. Következésképpen x’ sem egyenlő x-szel, és az éter nyugalmi állapotában lévő megfigyelő számára a mozgó nyugalmi állapotban megtett út rövidebb. Ennek semmi köze a tényleges fizikai távolságokhoz vagy rúdhosszokhoz. Nincs benne semmi rejtély. Valójában ha mindkét korrekciót egyszerre próbálja alkalmazni, ahogy azt a relativitáselmélet sugallja, akkor rossz eredményt kap.

A hossz-összehúzodás tehát hazugság. Kísérletileg soha nem figyelték meg, és nincs tudományos magyarázat arra, hogyan fordulhat elő a rúd rövidülése. A megfigyelt, megtett távolság órajel-különbségek miatti valós lerövidülését tévesen alkalmazták olyan objektumokra, amikor a mozgó referenciakeretben lévő objektumok nem tapasztalnak valódi összehúzódást. A gyorsabb órával rendelkező személy csak azt látja, hogy rövidebb utat tesz meg.

15. hazugság: Térösszehúzódás

A fizikában a 15. legnagyobb hazugság a térösszehúzódás. A térösszehúzódás, akárcsak a hossz-összehúzódás (14. hazugság), a speciális relativitáselmélethez kapcsolódó jelenség (13. hazugság). Észreveszed a mintát? A hosszúság összehúzódásával az éter nyugalmi keretben lévő megfigyelő, aki egy második referenciakeretben a fénysebesség szempontjából jelentős sebességgel mozgó objektumokat figyeli meg, a megtett távolság lerövidülését látja. Ez problémát okoz azon téves feltételezések szigorúan elkötelezett párthíveinek, akik szerint a fénysebesség minden megfigyelő számára azonos.

Hamis feltevésének megmentése érdekében Einstein azzal az ötlettel állt elő, hogy a hossz összehúzódásával a tér összehúzódott, és a fény valójában fénysebességgel mozog, mivel a tér méretei megváltoztak. Elmondása szerint a megfigyelőt csak becsapták azzal a gondolattal, hogy a fény rövidebb távolságra mozog, mivel a fénysebességnél lassabban mozog.

Ez a „logika” problémákba ütközik, amint van egy második megfigyelő, aki ugyanazt a teret figyeli. Tegyük fel például, hogy van egy millió megfigyelőd, akik millió különböző sebességgel mozognak ugyanahhoz a tárgyhoz képest, és mindegyikükhöz viszonyítva fénysebességgel vagy ahhoz közeli sebességgel mozognak. Ha a térösszehúzódás helyes lenne, akkor milliónyi különböző mennyiséget kellene egyidejűleg megrövidíteni.

A térösszehúzódás összeegyeztethetetlen a klasszikus geometriával, de két vagy millió különböző geometria egyidejűleg ugyanabban a térben nevetséges. Minden kritikus gondolkodási képességgel rendelkező személynek azonnal fel kell ismernie ezt tévedésként.

A térösszehúzódási hipotézis figyelmen kívül hagyja azt is, hogy a vákuumnak van energiája, ahogyan ezt Einstein is tagadta, aki a vákuum-ingadozások leghíresebb elutasítója is volt. A legenergetikusabb vákuum-ingadozások a legrövidebb hullámhosszúak. Elméletileg a hullámhosszaknak minden lehetséges hossza megvan, ami végtelen mennyiségű energiájú vákuumhoz vezet bármely tértérfogatban. Hagyományosan a Planck-hosszt (~10-35 méter) használják a lehető legkisebb hullámhossznak vagy határhullámhossznak, mivel nem vagyunk biztosak abban, hogy a fizika normál törvényei érvényesek-e ennél kisebb távolságokon is.

Ha a Planck-hosszt hullámhosszként egységnyi használjuk fel, akkor a vákuumenergia ~1095 gramm/köbcentiméternek felel meg. John Wheeler és Charles Misner eredetileg 1094 gramm/köbcentiméterként tette közzé, 32, de ennél az energiánál egy nagyságrend nem túl fontos. Az ősrobbanás modellje alapján a látható univerzumban jelenleg 1056 grammos becslések alapján a vákuum minden köbcentiméterének sokkal több energiája van, mint a teljes látható univerzumnak.

A vákuum-ingadozásoknak van hullámhossza és frekvenciája, és ezek hullámhosszai határozzák meg a tér fizikai méreteit. Az éter-nyugalmi-keret fizikai méretei minden irányban egységesek.

Nevetséges az az elképzelés, hogy egy gyorsan mozgó objektum valahogyan össze tudja szorítani ezt a sok vákuumenergiát, és megváltoztatja a tér méreteit azáltal, hogy megváltoztatja a vákuum-ingadozások hullámhosszát. Egy fotonnak egyszerűen nincs elég energiája ahhoz, hogy a tér összehúzódjon. Semminek sincs.

A térösszehúzódási hazugság oka ugyanaz, mint a hossz-összehúzódási hazugság. Az éter nyugalmi állapotában lévő megfigyelő, aki a fényt mozgó vonatkoztatási rendszerben figyeli, valóban látja, hogy a fény rövidebb távolságra mozog a mozgó keretben, miközben a vonatkoztatási rendszerében mért megfelelő távolságot mozog. A mozgó vonatkoztatási rendszerben lévő megfigyelő azt fogja látni, hogy a fény a megfelelő távolságra mozog, mert az ő órája lassan jár. Ennek semmi köze a hossz- vagy térösszehúzódáshoz.

Mint korábban, a fizikusok két lehetséges magyarázatot találhattak ki. Az első, amit kitaláltak, a hossz-összehúzódás volt, amelyet később kiterjesztettek a térösszehúzódásra is. A második lehetőség, amely nem sokkal később jött, az óra lassulása volt. Amikor megjelent az óralassulás, a fizikusok már kezdték elfogadni a hossz-összehúzódási modellt, és nem vették észre, hogy az óra lassulása önmagában a megoldás. Azt sem vették észre, hogy ha mindkét korrekciót alkalmazzák, rossz eredményt kapnak.

Nem lehet eléggé hangsúlyozni, hogy az éter nyugalmi állapota a standard viszonyítási keret. Viszonyítási nyugalmi keret nélkül lehetetlenné válik annak meghatározása, hogy melyik megfigyelő áll és melyik mozog. Szabványos referenciakeret nélkül az a probléma is felmerül, hogy kinek az órája gyorsabb és kinek a lassabb, ez az ikerparadoxon mögöttes problémája. Ha létezne olyan jelenség, mint a térösszehúzódás, akkor azt sem tudnánk, hogy melyik megfigyelő tere rövidülne meg. Még jó, hogy van egy szabványos referenciakeret, az éter nyugalmi állapota. Így van egy szabványunk két referenciakeret összehasonlítására.

A térösszehúzódás hazugság. A fénysebesség csak a nyugalmi kerethez képest mozgó megfigyelő számára tűnik azonosnak, mert az órájuk lassabb. A távolság mértékegységei a térben nem változnak, mert a vákuum-fluktuáció hullámhossza nem változik.

32 J. A. Wheeler és C. Misner, Geometrodynamics, Geometrodynamics, Academic Press, New York, 1962.

16. hazugság: A tér idődilatációja, időtágulása

A fizikában a 16. legnagyobb hazugság a tér idődilatációja. Ez nem azt jelenti, hogy nem létezik relativisztikus óralassulás. Az óra lassítása létezik, és kísérletileg is bebizonyosodott, leginkább a globális helymeghatározó rendszer (GPS) óráival. Míg sokan felváltva használják az „időtágulás” és az „óralassítás” kifejezéseket, van egy fontos különbség közöttük, és ez a megkülönböztetés azt sugallja, hogy az időtágulás hazugság.

Jól láthatóan a baj az éter elutasításából ered. Mivel Einstein, az éter-tagadó feltalálta a speciális relativitáselméletet a lorentzi relativitáselmélet helyett, hiányzott neki a fizikai magyarázat az óra lassulására. A vákuum-ingadozások nélküli univerzumban azonban az óra lassulása a tér miatt lelassult idő függvényének kell lennie. Ez azt jelenti, hogy ezek szerint magának a térnek van egy „órája”, amely lelassul, amikor mozog, és más, mechanikai és biológiai órák is lelassulnak. Tehát az idődilatáció, mint a tér tulajdonsága az, ami az idődilatációt hazugsággá teszi.

A speciális relativitáselméletben az idődilatációs koncepciónak van egy további problémája, mivel nincs preferált vonatkoztatási keret. Ha két vonatkoztatási rendszered van megfigyelőkkel, akkor mindkét megfigyelő azt gondolja, hogy mozdulatlan, a másik pedig mozog. Honnan tudja a tér, hogy mikor kell időtágítónak lennie? Természetesen ezt a problémát nem lehet megoldani egy univerzális szabványos referenciakeret, az éter nyugalmi kerete nélkül.

A lorentzi relativitáselméletben az éter létezik, így elmélete összhangban van az éter létezésére vonatkozó fizikai bizonyítékokkal. Ebben az esetben a mechanikus vagy biológiai óralassulás az éterrel való kölcsönhatások következménye. Az óralassulás egy fizikai jelenség, amely az éterrel való fizikai kölcsönhatásokkal magyarázható. Az óra lassulása tehát nem a tér mágikus tulajdonsága.

A fizikai mechanizmus megértése nem olyan nagy kihívás, ha példát a legegyszerűbb fizikai órával, egy forgó vákuum-ingadozási dipólussal kezdjük. Tekinthetünk egy dipólust, mint a fotonban lévőket. Ez a dipólus élettartama során 180 fokkal elfordul, hullámhossza és frekvenciája összhangban van a fénysebességgel, λv = c . A dipólusnak akkor van a leghosszabb hullámhossza, ha egy megfigyelő az éter nyugalmi állapotában/keretében nézi. Ugyanakkor frekvenciája, tulajdonképpen az órája, az éter nyugalmi állapotában leggyorsabb.

Egy mozgó vonatkoztatási rendszerben lévő megfigyelő számára a dipólus az éter nyugalmi keretben lévő éter-dipólusok mozgásával szemben mozog. Úgy tűnik, hogy az éter nyugalmi keret dipólusai valódi fizikai ellenállást fejtenek ki dipólusóránk mozgásával szemben. Úgy tűnik, hogy a dipólusóra rövidebb hullámhosszú (azaz a megtett távolság) egy álló megfigyelőhöz képest. Ugyanakkor az álló megfigyelő azt látja, hogy a dipólus forgási sebessége lelassul, ha egy mozgó megfigyelő szemszögéből nézi. Amint a dipólus lelassítja a frekvenciáját, lecsökken, és így az órája is lassabban jár.

A hullámhossz és a frekvencia szorzatának eredménye mindkét megfigyelőnél azonos, tehát ugyanazt a fénysebességet figyelik meg. Ők azonban a fényt más hullámhossznak látják. A mozgó megfigyelő számára a fény vöröseltolódott. A mozgó dipólus által tapasztalt óralassulás az éterrel való fizikai kölcsönhatásnak köszönhető. Illetve úgy gondoljuk, hogy a dipólus úgy viselkedik, mintha mindig az éter nyugalmi keretében lenne, miközben a mozgó megfigyelő órája lelassul az óra éterrel szembeni mozgása miatt.

A tér időtágulása hazugság. Hazugság azt állítani, hogy az üres térnek még órája is van. Az éter az óra, és az óra lassulása az éterrel való kölcsönhatásoknak köszönhető.

17. hazugság: hatás távolról

Hogy az egyik test távolról vákuumon keresztül, bármi más közvetítése nélkül hathat a másikra, és amelyen keresztül hatásuk és erejük egyikről a másikra közvetíthető, számomra ez olyan nagy abszurditás, hogy szerintem senki sem eshet ebbe bele, akinek filozófiai kérdésekben kompetens gondolkodási képessége van. 33

Sir Isaac Newton, 1693

A 17. legnagyobb hazugság a fizikában a távoli cselekvés vagy hatás. A távoli cselekvés egy másik a sok nagy hazugság közül, amelyek a vákuum-ingadozást elutasítók elméjéből születtek. Az elutasítók úgy gondolják, hogy a tér üres, ezért nem áll rendelkezésükre semmi, ami az erőátvitel közege lenne. Így megmaradt számukra a mágia elmélete, ahol az erők mágikus úton kerülnek át egyik helyről a másikra. Newton a legtöbb modern fizikussal ellentétben elég okos volt ahhoz, hogy felismerje, hogy a mágikus erőátvitel vagy a távoli cselekvés nem megoldás.

Newtont sem hibáztathatjuk azért, mert úgy döntött, hogy nem spekulál az erők átviteléről, mivel az ő korában nem volt meggyőző éter- vagy vákuum-fluktuációs elmélet. Voltak változatai a Descartes-i régi örvényelméletnek, és Nicolas Fatio de Duillier előállt egy elmélettel, amelyet később Georges-Louis Le Sage népszerűsített a vértestekkel kapcsolatban, 34 de mindkét elméletnek voltak problémái, és Newton bölcsen úgy döntött, hogy nem támogatja őket túl erősen. Miután Max Planck leírta a kvantumharmonikus oszcillátorokat, ami a vákuum-ingadozás fogalmához vezetett, a modern fizikusoknak nem volt mentségük arra, hogy ezt ne vegyék figyelembe.

A távolsági cselekvés vagy hatás elmélete rengeteg kérdést vet fel, mint például:

1. Hogyan ugrik a jel egyik helyről a másikra?

2. Hogyan küldik ezt a jelet úgy, hogy a jeladó test ne veszítsen energiát?

3. Milyen jel nem igényel energiát?

4. Hogyan történik az adatok tárolása és továbbítása?

5. Hogyan halad a jel az űrben?

6. Milyen gyorsan halad?

7. Hogyan fogadja a jelet a fogadó szervezet?

8. Hogyan dolgoz fel a fogadó szervezet számos jelből származó nagy mennyiségű adatot?

9. Hogyan mozog a fogadó test a jelekre reagálva?

10. Mi a mozgás mögötti energia forrása?

11. Mi a mozgásért felelős fizikai mechanizmus?

Ahogy Newton kijelentette, senkinek, aki képes a kritikai gondolkodásra, nem szabad hinnie a távoli mágikus cselekvésben. Túl sok megoldhatatlan problémát kell megoldani, ha valaki tagadja az átviteli közeg létezését.

Szerencsére léteznek vákuum-ingadozások, így az egész térben van egy közeg, amely erőket közvetít, és tárgyakat mozgat. Még Casimir által felfedezett modellünk is van arra, hogy az erők hogyan továbbítódnak a vákuumon keresztül. Ő tudományos ugrást hajtott végre annak felismerésében, hogy van der Waals erőkből származó vákuumnyomás van a vákuumfluktuációs dipólusok között. Ez a Casimir-van der Waals erő az összes tárgyat megnyomja, de az erő általában minden irányban azonos, ezért nem észlelhető, hacsak a nyomás nem lesz nagyobb vagy kisebb az anyagtestek közötti tartományban.

A távoli cselekvés vagy hatás hazugság. Az éter és a Casimir-van der Waals erők létezése azt bizonyítja, hogy nincs szükség távoli mágikus cselekvésre.

33 I. Newton, részlet Dr. Bentley-nek írt 1693. február 25-i leveléből.

34 N Fatio de Dullier, „De le Cause de la Pesanteur” (kb. 1690), szerkesztett változat, kiadó: K. Bopp, Drei Untersuchungen zur Geschichte der Mathematik, Walter de Gruyter & Co. 1929. 19-26. o.

18. hazugság: Mérőbozonok

A fizika legnagyobb hazugságai közül a 18. a mérőbozonok. A mérőbozonok a vákuum-ingadozás elutasítóinak téves válaszai a távoli cselekvés/hatás jelenségére, anélkül, hogy ténylegesen megoldanák a problémát. A mérőbozon-elméletben az erők a részecskék, melyek a mérőbozonok cseréjén keresztül közvetítődnek. Ezek a mérőbozonok hipotetikusan áthidalják a rést a térben, így az utasítások átkerülhetnek egyik objektumról a másikra.

Minden egyes erőtípushoz és a hozzá tartozó mezőhöz egy adott típusú mérőbozon tartozik. Vannak fotonok az elektromágneses erőkre, gravitonok a gravitációra, gluonok az erős erőkre és W és Z részecskék a gyenge kölcsönhatásokra. A 7. hazugság néhány okot fed le, amiért a fotonok nem lehetnek mérőbozonok.

Az első az energia megőrzésének a problémája, mivel egyik test sem veszít energiát a feltételezett részecskecsere során. Az energia-megmaradás elve nem sérthető meg. Következésképpen a mérőbozonoknak virtuális részecskepároknak kell lenniük, vagy ahogy itt is hivatkozunk rájuk, vákuum-ingadozásoknak. Vákuumingadozásként a mérőbozonoknak összhangban kell lenniük Planck kvantumharmonikus oszcillációs elméletével, és nem léphetik túl a Heisenberg-féle határozatlansági elv energia-idő korlátait. Ha a mérőbozonok meghaladják a Planck-oszcillációs energiát, akkor megsértik az energiamegmaradás elvét.

A legtöbb fizikus, aki támogatja a mérőbozon elméletét, kényelmesen elhagyja azt a követelményt, hogy a vákuum-ingadozások virtuális részecskepárokból álljanak. Minden párnak tartalmaznia kell egy anyag- és antianyag-részecskét, hogy az anyag és az antianyag egyensúlya megmaradjon. Minden párnak ellentétes töltésekkel kell rendelkeznie, hogy az elektromos semlegesség megfigyelhető legyen, vagy minden részecskének elektromosan semlegesnek kell lennie, feltételezve, hogy vannak olyan valódi elemi részecskék, amelyek semlegesek.

Ott van még a tömeg kényes kérdése is. Egyetlen részecskének, amelynek általában tömege van szabad állapotban, és amely elég sokáig él ahhoz, hogy meghaladja a Planck-energiát, tömeggel kell rendelkeznie. Ez korlátozza azt a távolságot, amelyet egy hipotetikus virtuális egyetlen részecske megtehet. Bizonyos nehéz nyomtávú bozonok esetében nem lehet azt gondolni, hogy rendelkeznek azzal a szükséges hatótávolsággal, amely szükséges ahhoz, hogy mérőbozon funkciójukat sértés nélkül betöltsék.

Ott van még a tömeg kényes kérdése is. Egyetlen részecskének, amelynek általában tömege van szabad állapotban, és amely elég sokáig él ahhoz, hogy meghaladja a Planck-energiát, tömeggel kell rendelkeznie. Ez korlátozza azt a távolságot, amelyet egy hipotetikus virtuális egyetlen részecske megtehet. Bizonyos nehéz méretű bozonok esetében nem lehet azt gondolni, hogy rendelkeznek a szükséges hatótávolsággal, hogy teljesítsék a mérőbozon funkciójukat anélkül, hogy megsértenék az energiamegmaradás elvét. Nagyon könnyű észrevenni e logika hibáit.

Ha a virtuális részecskepárok mérőbozonként működhetnének, akkor szinte végtelen hullámhossz- és energiatartománnyal kellene rendelkezniük. Egy adott energia vákuum-ingadozásának egy hullámhossza és egy frekvenciája van, mivel ezeket a tulajdonságokat egyetlen képlet rögzíti. Következésképpen egy két test közé feszített virtuális részecskepár csak egyetlen adatpontot hordozhat, a két test közötti távolságot.

Mint korábban említettük, a vákuum-ingadozás iránya és energiája nem mérhető egyszerre a Heisenberg-féle határozatlansági elv szerint. Egy elnyelő részecske nem tudja megmondani, honnan származik a feltételezett mérőbozon, hogy ismeri-e az energiáját, és hogy meg tudja-e határozni, honnan származik az energia, ez számára ismeretlen. Tehát bár egy virtuális mérőbozonnak lehet energiája és iránya is, mégis csak egyetlen bit adat továbbítására használható; ellenkező esetben a határozatlanság elve sérülne meg.

A mérőbozon ezért nem hordozhat információt a részecske tömegéről, töltéséről, fizikai méreteiről vagy bármilyen más olyan információról, amely az állítólagosan átvitt erő nagyságának és irányának meghatározásához szükséges.

A mérőbozonok hipotézise tehát nem írja le:

1. Hogyan keletkeznek mérőbozonok?

2. Hogyan marad meg az energia, az impulzus, a szögimpulzus, az anyag-antianyag, az elektromos töltés, a mágneses momentum vagy a spin?

3. Hogyan jutnak el messzebbre a tömegű mérőbozonok, mint amennyit az energiamegmaradás elve vagy a fénysebesség határa megenged?

4. Hol tárolják a mérőbozonok adataikat?

5. Hogyan haladnak a mérőbozonok energia felhasználása nélkül?

6. Honnan tudja a második részecske, hogy van-e mérőbozon?

7. Hogyan fogadja a második részecske a mérőbozont?

8. Honnan tudja a fogadó részecske, hogy a mérőbozon milyen messzire ment el és milyen irányból?

9. Hogyan méri vagy tölti le a fogadó részecske a mérőbozon adatait?

10. Hogyan számítaná ki a fogadó részecske az eredményt?

11. Milyen szuperszámítógéppel integrálják az egyidejűleg több milliárd méretű bozon adatait?

12. Hogyan korrigálja a fogadó részecske a fénysebesség késleltetését, mivel egy mérőbozon csak fénysebességgel tud továbbítani?

13. A számítás befejezése után hogyan mozog a test?

14. Honnan származik az energia, amivel a testet megmozgatja?

A mérőbozon hipotézise lényegében semmivel sem jobb, mint a távoli cselekvés vagy hatás. Sok ugyanazon teszten megbukik, mint ami nyilvánvaló az előző két fejezet listáinak összehasonlításakor is, és semmi esetre sem a teljesség igényével. A mérőbozon-elmélet nem ad megoldást a legtöbb alapvető problémára, hogy miképp lehetséges a távoli cselekvés vagy hatás. Ez csak a problémák természetét változtatja meg.

A mérőbozon-modell hazugság. A vákuum-ingadozások kontinuumának, az éternek kell lennie két test között ahhoz, hogy egy erőt közvetítsen. Newtont átfogalmazva: senki, aki képes a kritikai gondolkodásra, ne higgyen a mérőbozonokban.

19. hazugság: A tömeg belső tulajdonság

A fizikában a 19. legnagyobb hazugság az, hogy a tömeg egy belső tulajdonság. A tömeg minden részecske és anyag alapvető tulajdonsága. A tömeg az anyag mennyiségének mértéke. A tömeg a tömeggel függ össze, mivel a Földön a tömeg a gravitációból adódó gyorsulás tömegének szorzata, és az összes tömeget végső soron ennek gyorsításával mérik. Bármely test tömege a benne lévő részecskék tömegének összege, ami a legfontosabb, a legstabilabb részecskék, elektronok, protonok és neutronok. Az univerzumban az összes stabil anyag ebből a három részecskéből áll.

Ha figyelembe vesszük egy részecske tömegét, problémákba ütközünk. A fizika standard modellje nem tartalmazza a tömeg fizikai magyarázatát. A fizikusok meg tudják mérni a részecskék tömegét, beleértve az elektront, a protont és a neutront, de nem értik, hogy a részecskéknek miként van tömegük. Magyarázat hiányában a fizikusok a tömeget a részecske belső tulajdonságaként kezelik. A tömeg csupán annyi. Még Dirac egyenletében is a tömeg egyszerűen egy szám, amelyet nem valami még alapvetőbből származtattak.

A három legstabilabb részecske csak egy jéghegy méretű probléma csúcsa. Tudományos kísérletek alapján a standard modellen belül 3-féle tömegű elektron, 3-féle tömegű neutrínó, 6-féle tömegű kvark, 3-féle tömegű mérőbozon, 32-féle tömegű mezon és 75-féle tömegű barion létezik. 36 Ez összesen annyi, mint 122-féle tömegű részecske, és a standard modell egyiket sem magyarázza meg. És valószínűleg még sok minden van még, amit még kísérletileg meg kell erősíteni. De semmi esetre sem létezik 122+ belső állandó bármilyen alapvető elméletében.

A tömeget belső tulajdonságként kezelni tudományosan nem megalapozott; valójában ellenkezik a tudomány és a fizika definícióival. A tudomány megköveteli, hogy tanulmányozzuk a dolgok szerkezetét és viselkedését, a fizika pedig azt, hogy képesek legyünk fizikailag és matematikailag megmagyarázni ezt a szerkezetet és viselkedést. Valamit belsőnek nevezni hanyagság; a tudósok akkor nem végezték el a munkájukat.

Mint sok más hazugság, ez is, legalábbis részben, annak köszönhető, hogy a fizikusok figyelmen kívül hagyják az étert. Tudjuk, hogy a tömeg az energiához kapcsolódik az E = mc2 jól ismert egyenlet alapján, ahol c a fénysebesség, E és m pedig energia és tömeg. Ez az egyenlet azt jelenti, hogy képesnek kell lennünk megérteni és fizikailag megmagyarázni a tömeget az energia szempontjából. Az éterelutasítók azonban, akik egy elektront vagy egy protont teljesen üres térben vélnek, megrekednek. Nincs mód a tömeg, mint energia modellezésére, ha a részecskében és körülötte nincs energiaforma.

Szerencsére tudjuk, hogy a vákuum-ingadozások nullponti energiaként léteznek, és a nullponti mezőt, más néven étert alkotják. Még akkor is, ha a Planck-hosszt használják határhullámhosszként, a vákuum energiája ~1095 gramm/köbcentiméter. Ez megnyitja annak lehetőségét, hogy a tömeg modellezhető az éter energiájával kapcsolatban. Őszintén szólva ez az egyetlen fizikailag valós lehetőségünk.

Az is szerencsés, hogy a múlt század egyik legzseniálisabb fizikusa, Dirac már előállt a tömeg magyarázatának ötletével. Dirac úgy gondolta, hogy egy részecske energiája annak az energiának köszönhető, amelyre szüksége van ahhoz, hogy megtartsa helyét a Dirac-tengerben. A Dirac-tenger az elektronokból és pozitronokból álló éter hipotetikus formája volt. A részecskéket nyomja, és a részecskéknek bizonyos mennyiségű energiával kell rendelkezniük, hogy visszanyomják és megtartsák helyüket a Dirac-tengerben. Feltételezte, hogy a „visszatolási” energia a részecske tömege. Sajnálatos módon úgy tűnik, hogy sem ő, sem senki más nem foglalkozott azzal, hogy elvégezze a számítást, hogy megnézze, helyes-e a modellje, egészen 2011-ig, míg magam el nem végeztem.

A legegyszerűbb módja annak, hogy Dirac modelljét könnyen kiszámítható formába helyezzük, ha feltételezzük, hogy a részecske olyan, mint egy gömbhéj. Ekkor felismerhetjük, hogy a héj bármely átmérőjével megegyező vákuum-fluktuációs hullámhossz nem létezhet benne vagy körül. Ezeket a hullámhosszakat ugyanúgy kizárják, mint két párhuzamos lemez között, mint a Casimir-effektusnál. Lényegében egy részecske héjszerű modelljét Casimir-üregként kezelhetjük, és mérhetjük az energiát.

A protonnak ismert töltési sugara van, így ez jó kiindulási pont neki. Az elektron viszont egy kicsit zavaróbb, mivel amikor fényt vagy elektronokat szórunk le egy elektronról, úgy tűnik, hogy fizikai méretű. Az elektron tömege is egy hullámhossznak, a Compton-hullámhossznak felel meg, amely sokkal nagyobb, mint egy proton. Másrészt, ha protonokat szórunk le egy elektronról, az sokkal kisebbnek tűnik, mint a proton, és talán még egy pont is. A ponttömeg-hipotézis nehézségeivel a következő fejezet foglalkozik.

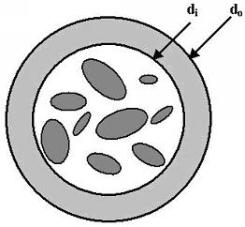
19-1. ábra A részecskehéj illusztrációja ellipszis alakú vákuum-ingadozásokkal a közepén, valamint a belső és külső gömbhéjakat leíró körök átmérőjével.

A számítás azt mutatja, hogy a proton tömege egyenlő a vákuumenergiával, amelyet a proton töltési sugarának átmérőjű héj kizár. Az elektron tömege megegyezik azzal a vákuumenergiával, amelyet a Compton-hullámhossznak megfelelő vagy ahhoz közeli héj kizár. Vegye figyelembe, hogy az elektron töltési sugarát formálisan soha nem határozták meg ezen a skálán szórási kísérletekkel. A tömegek aránya, a fizika egyik nagy rejtélye, egyszerűen a vákuumenergia és a részecskék sugarának függvénye. Ezt részletesebben a Casimir-üreg által kiszorított vákuumenergiaként kapott proton- és elektrontömeg című írásomban fejtem ki. 37

Kiderült, hogy Diracnak igaza volt a tömegenergiára vonatkozó hipotetikus részecskemodelljében, de szomorú, hogy 80 évbe telt, mire valaki elvégezte a számítást, hogy ezt bebizonyítsa. Mivel a neutron mérete hasonló a protonhoz, tömegét hasonló módon magyarázzák.

Az univerzum stabil tömegét alkotó három fő részecske tömegét nagyon egyszerűen megmagyarázzák egy eredetileg Dirac által leírt modellel. A tömeg az eltolt vákuumenergia. El kell ismerni, hogy léteznie kell egy másik típusú vákuumenergia-elmozdulásnak az instabil „részecskék” tömegének, a rezonanciáknak a leírására, de legalább van egy út előre, és jó okunk van azt gondolni, hogy tömegük modellezhető, valamint egy tulajdonság nullponti energiájú. Erre később visszatérünk.

A belső tömeg fogalma hazugság, mivel minden részecsketömeget meg kell magyarázni fizikai és matematikai módon is. A fizika tudománya megköveteli ezt. Az is hazugság, hogy a proton-, elektron- vagy neutrontömeg alapvető állandók.

36 A Wikipédia szerint a mezonok és barionok listái.

37 R. Fleming, „A proton- és elektrontömeg a Casimir-üreg által eltolt vákuumenergiaként származtatott”,

https://www.researchgate.net/publication/283795493_Proton_and_electron_mass_derived_as_the_vacuum_energy_displaced_bymir_20_Cityas_imir_20_acav , 2012

20. hazugság: Tömegpont

A fizikában a legnagyobb hazugságok 20. része a tömegpont. A szabványos modellfizikában a fizikusok alapvetően felhagytak azzal, hogy a részecskéket fizikai testként írják le, és a részecskéket pontként, más szóval fizikai dimenzió nélkül kezelték. A tömegpont-hipotézis annyira abszurd, hogy megérdemli a helyét a fizika legnagyobb hazugságai között.

Az első nehézség a sűrűség. Ha először egy kis térfogatú részecskét veszünk számításba, és a tömeget ezen a térfogaton belül egyenletesen eloszlónak tekintjük, akkor kiszámíthatjuk a sűrűségét, az egységnyi térfogatú tömeget. És ahogy ez a feltételezett részecske egyre kisebb lesz, a sűrűsége növekszik. Ha viszont egy pontszerű részecskének tekintjük, akkor a sűrűsége végtelen lesz, ám a tömegsűrűség soha nem lehet végtelen.

Itt fontos megjegyezni, hogy az egydimenziós modell, mint például a húrelméletben, nem segít. Még mindig több mint 122 különböző egydimenziós húrunk van, és csak úgy lehet feloldani őket, hogy egységnyi hosszonként eltérő tömeggel rendelkezünk. De az egységnyi térfogatra eső tömegsűrűség még mindig végtelen és irracionális. Az egyetlen módja annak, hogy elkerüljük az irracionális végtelen problémát, ha háromdimenziós részecskemodellünk van.

Ezután figyelembe kell vennünk, hogy ha a részecskék tömegét modellezzük, akkor ennek a modellnek vákuumenergiát kell tartalmaznia, mivel a nullponti energia valóban létezik, és végső soron minden energia alapvető forrása. A részecsketömeg leírásához a részecskéknek térfogattal kell rendelkezniük, és ha van térfogatuk, akkor vákuumenergiát váltanak ki. És ahogy Dirac feltételezte, az eltolt energia részecske-tömeg-energia.

Tehát, ha például egy elektronnak 10-15 méter átlagos átmérőjű klasszikus sugarú gömbhéja van, akkor tömege alig lesz kisebb, mint a protoné. Ha 10-18 méter átmérőjű héja van, akkor 1000-szer nagyobb tömegű, mint egy proton, 10-21 méternél pedig milliószoros tömegű. Ha akkora, mint a Planck-hossz, ~10-35 méter, akkor egy kis fekete lyuk lesz.

Ne feledjék, hogy ha egy részecskét szilárd gömbként, nem pedig héjként modelleznénk, akkor a tömeg végtelen lenne, mivel a legkisebb vákuum-ingadozás is kizárt lenne. Ugyanez a probléma a végtelenül sima gömb alakú héjnál is előfordul, mivel a héjon belüli kis vákuum-ingadozások szintén kizártak. A részecske héjszerkezetének, bármilyen legyen is az, porózusnak kell lennie a kis vákuum-ingadozásokkal és a részecskékkel szemben.

A tömegpont fogalma hazugság. Lehetetlen modellezni egy pontszerű részecske tömegét, mivel végtelenül sűrű és végtelen tömegű lenne. Reálisabban nézve nem lenne tömege. A részecskéknek valós fizikai térfogattal kell rendelkezniük.

21. hazugság: Az anyag és az antianyag belső tulajdonság

Saját véleményem az, hogy nem csak a jelenlegi kvantummechanikánkban, hanem tulajdonképpen a klasszikus mechanikában is alapvető változtatások módját kell keresnünk. Mivel a klasszikus mechanika és a kvantummechanika szorosan összefügg, úgy gondolom, hogy még tanulhatunk a klasszikus mechanika további tanulmányozásából. Ebben a nézőpontban eltérek néhány elméleti fizikustól, különösen Bohrtól és Paulitól. 38

Paul Dirac, 1949

A fizika legnagyobb hazugságai közül a 21. az az elképzelés, hogy az anyag és az antianyag belső tulajdonságok. Dirac értelmezése szerint a Dirac-egyenlet megoldásainál az anyag és az antianyag pozitív és negatív „energia” kapcsolatban áll egymással. A legtöbb mainstream fizikus azonban nem próbálja megérteni ezt az „energia” kapcsolatot, és egyszerűen az anyagot és az antianyagot belső tulajdonságként kezeli. Bár ez a felszínen jelentéktelennek tűnhet, óriási hiba, talán a második legnagyobb az éter tagadása után.

A Dirac-féle elektronegyenlet a 20. század fizikájának egyik nagy diadala volt. Elgondolkodtató azonban, hogy volt pozitív és negatív „energia” megoldása is, és nem volt ismert olyan körülmény, amely tiltaná a negatív „energia” megoldást. Dirac negatív és pozitív „energiaként” értelmezte őket, de senki sem tudta biztosan, hogy ez mit jelent. Mindenesetre a negatív „energia” megoldást ma már elfogadják a pozitron előrejelzéseként, bár Dirac elismerte, hogy nem volt elég bátor ahhoz, hogy közzétegye ezt a jóslatot. A fizikatörténészek kedvesek voltak hozzá, és mindenesetre megérdemelten adták neki ezt az elismerést.(Ford: hogy pozitron létezését megjósolta.)

A negatív „energia” megoldás rejtélyes volt és továbbra is rejtélyes, mivel a valódi energia minden formája pozitív. Dirac úgy kerülte meg a problémát, hogy elképzelte, hogy a vákuum virtuális pozitív és negatív elektronok tengeréből, az úgynevezett Dirac-tengerből áll. Mint láttuk, modellje nem állt messze az általunk megismert igazságtól. A Dirac-tenger modellje a nullpont mező és az éter korai modellje volt, és már a kezdetekben előrelépéshez vezethetett volna a fizikában, ha azt komolyan vették volna.

Dirac ezután az elektront és a pozitront lyukként látta a Dirac-tengerben, ami a tömeg egyszerű matematikai levezetéséhez vezet, amelyet a 19. fejezetben ismertetünk. Míg Dirac a tömegenergiát magyarázta, valójában nem foglalkozott sikeresen az egyenletének pozitív és negatív, anyag és antianyag „energia” megoldásával.

Dirac megpróbálta modellezni egyenletének pozitív és negatív „energia” megoldásait a Dirac-tengeri modellje segítségével. Úgy vélte, hogy a negatív energiájú tér felett létezhet egy pozitív energiatér, amelyet egy nulla energiájú tartomány választ el, és a semleges zóna felett elektronok, alatta pedig pozitronok találhatók. Az anyag és az antianyag ekkor ellentétesek, de egyenlők lehetnek valamiben, amit anyag-energiaként fogunk fel, és a megsemmisülés révén kiolthatják egymást.

21-1. ábra A Dirac-tenger szemléltetése, ahol virtuális részecskepárok találhatók a nulla energiát jelző vonal ellentétes oldalán. A fekete körök pozitívak, a szürke körök pedig negatívak.

Alternatív megoldásként az anyagot a térben lévő buboréknak, az antianyagot pedig lyuknak képzelte el, így ezek egyenrangúak, de bizonyos szempontból ellentétesek. Ebben a modellben egy buborék kitölthet egy lyukat, és azt a teret normál vákuummá alakíthatja. Ebben a modellben a lyuk és a buborék semlegesíti egymást egy megsemmisítési folyamat során.

Itt akadtak el Dirac ötletei. Az éter-elutasítók bár hajlandóak voltak meghallgatni Diracot a ragyogása miatt, de nem győzték meg őket, hogy éterszerű Dirac-tenger valódi lehet. Buborék- és lyukmodelljeit puszta érdekességnek tekintették, bár ezt mindig új fizikusok generációival is megismertették.

Ennek megértéséhez először is emlékeztetnünk kell arra, hogy bár Dirac a pozitív és negatív megoldásokat „energiaként” írta le, ezek nem az energiát képviselik, ahogyan azt általában definiálják. Az anyaghoz és az antianyaghoz kapcsolódó új típusú „energiát” talán anyag-energiának kellene nevezni, hogy elkülönítsük.

Talán az elektromos töltés is hasonló matematikai módon modellezhető, mint az anyag és az antianyag a Dirac-egyenletben. Az anyag és az antianyag ugyanolyan típusú kapcsolatban áll egymással, mint a pozitív és a negatív elektromos töltés, miközben teljesen különálló részecsketulajdonságot képviselnek.

Hazugság az az állítás, hogy az anyag és az antianyag belső tulajdonság. A fizikusok lemaradtak egy fontos felfedezésről, amikor úgy döntöttek, hogy figyelmen kívül hagyják a Dirac-egyenlet negatív megoldásainak következményeit. A Dirac-egyenlet értelmezésében és az elektron még felfedezésre váró szerkezetében rejlik az anyag fizikai magyarázata. Amint látni fogjuk, még sokat kell tanulni a pozitív és negatív anyag-energia kölcsönhatásokról.

38 P.A.M. Dirac: A klasszikus és a kvantummechanika kapcsolata. Proceedings of the Second Mathematical Congress, Vancouver, 1949. Toronto: University of Toronto Press. old. 18 (1951).

22. hazugság A tehetetlenség belső tulajdonság

Mert függetlenül attól, hogy van-e lényegileg anyagi tehetetlenség, vagy nincs, minden bizonnyal van elektromos tehetetlenség. […] Valószínűleg nincs is más. Valószínűleg az, amit a közönséges anyag tehetetlenségeként észlelünk, egyszerűen hatalmas számú iontöltés, vagy elektromos atom vagy elektron elektromos tehetetlensége vagy önindukciója. Ez messze a legérdekesebb hipotézis, mert lehetővé teszi számunkra a fejlődést, és határozott. A tulajdonságok keveredése – részben megmagyarázva, ti. az elektromos, részben megmagyarázhatatlan, ti. az anyag – sehova sem vezet bennünket. 39

Oliver Lodge, 1906

A fizikában a 22. legnagyobb hazugság az, hogy a tehetetlenség saját tulajdonság. A tehetetlenség a test azon tulajdonsága, hogy megtartja sebességét, hacsak nem reagál rá. Mint a fizika sok nagy hazugsága, itt is a vákuum-ingadozás elutasítói állnak a háttérben. A nullponti mezőt vagy étert alkotó vákuum-ingadozások nélkül a vákuummodelljükben semmi sem képes kölcsönhatásba lépni egy testtel, ami tehetetlenséget okozna. A visszautasítók ekkor megrekednek a tehetetlenség tényében, amely mintegy varázsütésre történik az anyagban, számukra teljesen megmagyarázhatatlan módon.

Ennél is rosszabb, hogy a vákuum-ingadozás elutasítói nem hajlandók feltenni a kérdést, és lekicsinylik azokat, akik ezt teszik. Ez nagyon szomorú és nem tudományos eljárás, mivel a tehetetlenség a mechanikai erők elméletének a sarokköve. Nincs mindenre elmélet a tehetetlenség fizikai magyarázata nélkül.

Az egyik fő oka annak, hogy a korábbi kísérletek, amelyek a tehetetlenséget a vákuum-ingadozásokkal való kölcsönhatásként írták le, kudarcot vallottak, az az, hogy fotonpárokként modellezték őket. Amint az 5. hazugságban kifejtésre került, a nullpont mező nem állhat fotonpárokból, mivel a virtuális fotonpárok bármely fizikailag valós modellje meghaladja a kvantumharmonikus oszcillátor energiáját, és így meghaladná a Planck-energiát és a Heisenberg-féle bizonytalansági elvet, és így megsértik az energiamegmaradás elvét.

A vákuumfluktuációk valódi virtuális részecskepárok, például elektron-pozitron és proton-antiproton párok. Ezek a részecskepárok elektromos töltési dipólusokat alkotnak, és olyanokat alkotnak, amelyeket anyag-antianyag dipólusoknak tekinthetünk. Ha visszamegyünk a Dirac-féle elektronegyenlethez, akkor az elektronok pozitív „energia”, a pozitronok pedig negatív „energia” megoldást jelentenek. Az anyag és az antianyag az „energia” egyenlő, de ellentétes formája, és kioltják egymást. Valóban olyan dipólust alkotnak, amely határozottan különbözik az elektromos töltés dipólusától.

22-1. ábra A huzalon belül mozgó elektronok a környező vákuumfluktuációs dipólusokban forgást váltanak ki. A vákuumfluktuációs dipólusok forgása áramot indukál a vezetékben.

Van egy jelenség az elektromágneses elméletből, amely nagyon hasonló, ha nem azonos a tehetetlenséggel. Ez a jelenség az önindukció. Ha egy zárt áramkörben folyó áramot tekintünk, akkor az áram mágneses teret indukál a vezeték körüli éterben. A vezeték körüli mágneses tér is áramot indukál a vezetéken. Egy hipotetikus veszteségmentes áramkörben ez az önindukció a végtelenségig folytatódhat, ugyanúgy, ahogy egy mozgó test vákuumban, vagyis üres térben a végtelenségig mozoghat.

Bár az is igaz, hogy az egyébként elektromosan semleges anyagtestek elektromosan töltött részecskékből állnak, ha szubatomi léptékben nézzük, a test még mindig semlegesnek tűnik bármilyen távolságban, és nem hoz létre mágneses teret, amikor mozog. A tehetetlenség nem lehet közönséges elektromágneses önindukció.

22-2. ábra Egy vonal mentén mozgó anyag, amely a környező vákuum-ingadozásokban forgást vált ki.

Az anyagtestek azonban anyagok, és mint ilyenek, kölcsönhatásba léphetnek Dirac anyag-antianyag dipólusával, feltételezve, hogy Dirac „energia” értelmezése érvényes. Ha így igaz, akkor a tehetetlenség egyszerűen önindukció az anyag-antianyag kölcsönhatás keretein belül. Ha a dipólus nem anyag és antianyag, akkor erős érvelés lehet, hogy léteznie kell valamilyen nem elektromos dipólusnak, hogy megmagyarázza a tehetetlenséget és más mechanikai erőket. De ha megvizsgáljuk az elektron-pozitron pár összes tulajdonságát, akkor csak két dipólus létezik, amelyek két ellentétes típusú töltéssel vagy „energiával” rendelkeznek. Tehát az összes lehetőség közül a legegyszerűbb az, hogy a tehetetlenség egyfajta anyag-antianyag önindukció.

Az az állítás tehát, hogy a tehetetlenség belső tulajdonság, hazugság. A tehetetlenség anyag-antianyag dipólus magyarázatával vagy anélkül, világos, hogy hamis az az elképzelés, hogy a tehetetlenség a testben rejlene. A tehetetlenséget olyan testnek kell tekintenünk, amely az önindukcióval összhangban kölcsönhatásba lép a nullponti mezővel.

39 O. Lodge, Electrons or The Nature and Properties of Negative Electricity, George Bell and Sons, London, 1906.

23. hazugság: Nincs mechanikus erő

A fizikában a 23. legnagyobb hazugság az, hogy nincs mechanikai erő. Ha megnézzük a standard modellben szereplő négy alapvető erőt, az elektromágneses, a gravitációs, a gyenge és az erős kölcsönhatást, akkor a mechanikai erőket nem veszik figyelembe. És így, hogy a mechanikai erőket nem vették fel az alapvető erők listájára, a standard modell fizikájának egyik legnagyobb baklövése, mivel így az alapvető erőket nem lehet egyesíteni a mechanikai erők bevonása nélkül.

Newton második törvénye, az F = ma, az erő egyenlő a tömeggel és a gyorsulással, a tehetetlenség utáni mechanikai erő legegyszerűbb matematikai ábrázolását adja. Ezt az erőegységet az ő tiszteletére Newtonnak nevezik. A leggyakoribb mechanikai erő, amellyel nap mint nap szembesülünk, egy tárgy súlya, ahol a gyorsulás a gravitáció miatti gyorsulás.

A mechanikai erők voltak a legkorábbi matematikailag leírható erők. Éppen ezért olyan zavarba ejtő, hogy a mechanikai erőket nem említik az úgynevezett alaperők között. A legvalószínűbb bűnös az, hogy sok fizikus zárt elméletnek tartja a mechanikai erőket. Azt hiszik, már mindent tudnak a mechanikáról, amit tudniuk kell. Mint láttuk, ez nem így van. Nem is értik a tehetetlenséget, a legalapvetőbb mechanikai erőelvet.

A másik hibája az, hogy az elektromossággal és a mágnesességgel ellentétben a mechanikának soha nem volt Michael Faraday pillanata, aki felállt és azt mondta: aha, kell lennie valami mezőnek, ami megmagyarázza az erőket. Ahogyan azt a 22. hazugságnál tárgyaltuk, a tehetetlenségi modell minden racionális tárgyalása egy mező létezéséhez vezet.

Kell lennie egy mezőnek, amely megmagyarázza a tehetetlenséget. Amikor egy test áthalad a térben, mezőt hoz létre az éterben, majd az éterben lévő mező mozgásra készteti a testet. Ez a mechanikus önindukció egyik formája. Valamiféle mező nélkül nincs reményünk a tehetetlenség sikeres modellezésére. Emellett mechanikai tér nélkül nincs remény az elektromágneses és a mechanikai erőelmélet egyesítésére.

A hiányzó mechanikai mező könnyen felismerhető egy búgócsiga vagy giroszkóp tanulmányozásakor. Talán ezért lepnek meg minket annyira ezeknek a működése. Ahogy a csúcsánál el kezd forogni, majd imbolyogni kezd, miután a gravitáció felgyorsítja. Ez a gyorsulás azonban a gravitációra merőleges, a csúcs precessziós irányába mutató mozgássá alakul át, ami megegyezik a csúcs forgási irányával.

Ekkor a precesszió irányú gyorsulás felfelé irányuló gyorsulássá alakul, amely ellentétes a gravitációval. A mechanikában Newton második törvényének megfelelően, ha van gyorsulás, van erő is. A búgócsiga a gravitációval ellentétes mechanikai erőket hoz létre. A fizikusok szeretik ezt forgatónyomatéknak nevezni, és úgy tesznek, mintha valami kisebb lenne, mint egy valódi erő, csak egy úgynevezett álerő.

A csúcsnak azonban valami ellen kell hatást gyakorolnia. És mivel a vákuumban mechanikai erők léteznek, a forgó csúcsnak valamilyen módon meg kell ragadnia a vákuumot, vagy konkrétan a vákuum ingadozásait. Kell lennie egy mezőnek, és a mezőnek vákuum-ingadozásokból kell állnia. A csúcs még az elektromosságra és a mágnesességre vonatkozó szabályokat is betartja, beleértve a hasonló típusú mezőket a polarizációval és a vákuumdipólusok forgásával. Ennek a jellegzetes forgó csúcsnak természetesen nincs nettó elektromos töltése, és nem hoz létre elektromágneses teret, ezért kell lennie más típusú dipólusnak és más típusú mezőnek.

A 19. század vége óta sok fizikus, köztük Oliver Heaviside, Robert Forward és Martin Tajmar felismerte, hogy a mechanikai erőelmélet az elektromossághoz és a mágnesességhez hasonló módon írható le. 40,41,42 Mindegyikük megpróbált kialakítani a mechanikai erő és a gravitáció egyesítése révén egy gravitomágneses elméletet.

Ezek az elméletek nagyrészt kudarcot vallanak a rossz irányban működő gravitáció miatt. Ellentétben az elektromos töltésekkel, a tömeget gravitációs esetben vonzza, nem pedig taszítja. Ezekből az elméletekből hiányzik a töltésszerű dipólus is, így az ellentétes töltések vonzzák, a hasonló töltések taszítják. Nincs negatív tömeg vagy negatív gravitáció.

Ha lenne egy megfelelő irányú erő ahhoz, hogy egy elektromágneses-szerű mechanikai erőelmélet működjön, az azt jelentené, hogy az univerzum gyorsuló ütemben tágulna. Ó várj, ez van.

Ez azt is jelentené, hogy az azonos irányban, egymás mellett haladó csillagok vonzódnának egymáshoz, és a forgó galaxisokban a csillagokra egy mechanikus Lorentz-szerű erő hatna, amely a legnagyobb tangenciális sebességű csillagokat a galaktikus mag felé löki. Ez a két hatás arra kényszerítené a forgó galaxisokat, hogy spirálokat alkossanak, tehát tudjuk, hogy ez helytelen. Hoppá, nos, a fizikusoknak nem kellett volna semmi ilyen nyilvánvalót kihagyniuk. Vicces, hogy ha van egy mechanikai tér és a hozzá kapcsolódó dipólus, akkor a mechanika összes fontosabb megoldatlan problémája könnyen megoldható.

A mögöttes problémák az voltak, hogy a fizikusok nem voltak tudatában a töltésszerű dipólusnak, amely a mechanikai erőelmélethez illik, és a legtöbb fizikus nem tudta felfogni, hogy a mechanika térerő. Kísérletek történtek annak magyarázatára, hogy az elektromos dipólusok miként magyarázhatják a mezőszerű mechanikai kölcsönhatásokat. Ám ezek eddig kudarcot vallottak. Tehát egyelőre csak azt mondhatjuk, hogy ez a mechanikai térerőtér nem az elektromos dipólusoknak köszönhető.

Amikor Dirac előállt az elektron egyenletével, amely pozitív és negatív „energia” elektronokat is megjósolt, egy új lehetőség nyílt meg. Az új részecske pozitronként, a negatív „energia” formája pedig antianyag néven vált ismertté. A fizikusok nem ismerték fel, hogy ezek a pozitív és negatív „energia” megoldások, amelyek az anyagot és az antianyagot képviselik, úgy néznek ki, mint egy új és más típusú töltések, mint egy új dipólus.

Egyes fizikusok egy másik dipólust akarnak javasolni. Megnézhetik egy elektron és pozitron tulajdonságait az alábbi táblázatban, és kiválaszthatnak egyet, de nincs más jó jelölt az ismert részecsketulajdonságok közül. Azt hiszem, valami új sci-fi elméletet alkothatnának helyette, ahogy szokták.

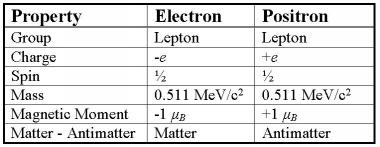
23-1. táblázat Az elektron és a pozitron ismert alapvető tulajdonságainak az összehasonlítása.

A mechanikai erő tagadása valóban az egyik legnagyobb hazugság a fizikában. Minden bizonnyal létezik mechanikai erő, és számos jelenséget le kell írnunk a mechanika területén. Ahhoz, hogy a mechanikai erőelmélet megmagyarázza a testek és a vákuum kölcsönhatását, és hogy egyesüljön az elektromágneses erőelmélettel, a mechanikai erőket térelméletként kell kezelni. Mechanikus dipólusnak kell lennie. További információkért olvassa el az Electro-Matter Force című írásomat vagy a The Zero-Point Universe című könyvemet.43.

40 O. Heaviside, "A gravitációs és elektromágneses analógia" The Electrician 31: 81–82 1893

41 R.L. Forward, "General Relativity for the Experimentalist", Proceedings of the IRE, 892-586, 1961.

42 M. Tajmar et al, Coupling of Electromagnetism and Gravitation in the Weak Field Approximation, Physica C 385:551-554 2003.

43 R. Fleming, „The Electro-Matter Force”,

https://www.researchgate.net/publication/284179658_The_Electro-Matter_Force  , 2012

24. hazugság: A fizika megmagyarázza a mechanikai mozgást

Minden tapasztalatunk, kivétel nélkül, azt a tételt erősíti, hogy egyetlen test sem mozog semmilyen irányban vagy semmilyen módon, kivéve, ha valamilyen más, vele érintkező test nem hat rá a saját mozgásával. […] Matematikai okokból néha kényelmes volt úgy kezelni egy problémát, mintha az egyik test tudna hatni a másikra anélkül, hogy fizikai közeg lenne közöttük; de egy ilyen felfogásnak nincs racionális oka, és nem ismerek senkit, aki ezt tényként hiszi el. Ha ez megadatott, akkor filozófiánk megegyezik tapasztalatunkkal, és minden test azért mozog, mert hatnak rá, és mindenféle jelenség mechanikai előzménye valamilyen szomszédos, energiával rendelkező testben keresendő; vagyis a nyomás vagy nyomás előidézésének képessége. 44

Amos Emerson Dolbear, 1897

A fizikában a 24. legnagyobb hazugság az, hogy a fizika megmagyarázza a mechanikai mozgást. Ez egyenértékű az elektromágneses elméletben ugyanazzal a problémával (9. legnagyobb hazugság), de a mechanikai mozgás esetében. A fizikusok úgy tesznek, mintha tudnák, hogyan mozognak a csúcsok és a giroszkópok, mert ki tudják számítani az eredményt, pedig valójában nem értik, hogyan lépnek kapcsolatba a forgó tárgyak az éterrel, és hogyan nyomulnak neki.

Az elektromágneses elmélethez hasonlóan a fizikusok többsége a mechanikai elméletet lezártnak, teljes elméletnek tekinti, amelyet soha többé nem szabad megvizsgálni. Ne feledje, hogy nem tudnak még egy olyan egyszerű dolgot sem megmagyarázni, mint a búgócsiga. Következésképpen soha nem jutottak el ahhoz, hogy leírják, hogyan mozognak a testek fizikailag mechanikai erők hatására, amikor nincs fizikai érintkezés. És vegye figyelembe: szubatomi szinten még a fizikai érintkezés sem az, mint aminek látszik.

Amint azt korábban említettük, a fizikusok soha nem ismerték fel, hogy a mechanikának térerőnek kell lennie, még kevésbé találtak ki egy fizikai modellt a mezőkre. Aztán a tényleges mozgás tekintetében elhanyagolták azt a kérdést, hogy mit jelent az erőhatás és hogyan jön létre ez az erőhatás? Vagy ha megkérdezték, gyorsan elhallgattatták őket, és azt mondták, hogy ne aggódjanak az ilyen dolgok miatt; eretnekség megvitatni. Szerencsére léteznek vákuum-ingadozások, egy térerő részeként kölcsönhatásba lépnek, és az elektromágneses erőkhöz hasonlóan tökéletes közeget alkotnak a mechanikai erők átvitelére az egyébként fizikailag nem érintkező testek között.

Akárcsak az elektromágneses erőmozgás esetében, Casimir volt az, aki anélkül, hogy észrevette volna, kitalálta a mechanikai erők működésének alapjait a vákuumenergiára adott válaszként. A vákuumfluktuációs dipólusok van der Waals erőket hoznak létre, és ezek az erők a testeket nyomják. A mechanikai erőkben egyszerűen más a dipólusunk. A dipólus kivételével az elvek pontosan ugyanazok.

Az elektromos dipólusokhoz hasonlóan a mechanikai (anyag-antianyag) dipólus miatti van der Waals nyomáserő megváltozik, ha bizonyos vákuum-ingadozásokat kizárunk a tér egy tartományából. Ne feledje, hogy az elektromos és mechanikus dipólusoknak valamilyen módon különbözniük kell ahhoz, hogy a mechanikai mozgás ne hozzon létre elektromágneses teret. Nem fogok ezen itt spekulálni, mivel ez végső soron a részecskeszerkezet kérdéseibe kerül, azon kívül, hogy az elektromos töltés és az anyag töltése bizonyos szempontból merőlegesnek tűnik egymásra. Mindenesetre meg kell határoznunk a mechanikai töltés nagyságát, és származtatnunk kell vagy kísérletileg meg kell határoznunk a megfelelő állandókat a mechanikai erőegyenletekhez.

Az elektromágneses erőkhöz hasonlóan két ellentétes mechanikai töltésű test polarizálja a köztük lévő vákuum-ingadozásokat. Aztán ahogy a dipólusok összeérnek és megsemmisülnek, a mellettük lévő dipólusok közelebb kerülnek egymáshoz. Ez a van der Waals nyomás csökkenéséhez vezet két ellentétes töltésű test között. Ekkor a külső nyomás összenyomja a testeket.

Ha két hasonló töltés (pl. mindkettő anyag) létezik a tér egy tartományában, a vákuum-dipólusok a középső pontban egymással szemben állnak, ami a közöttük lévő van der Walls-erő nyomásának a növekedéséhez vezet, ami a testeket széttolja, és a nyomás leküzdésével egymáshoz nyomja őket.

Ahogy a 22. hazugságban a tehetetlenséggel kapcsolatban említettük, a tehetetlenség az önindukció egyik formája. A mechanikus mozgás hatására a mechanikus dipólusok elfordulnak, a mechanikus dipólusok pedig a tárgyak mozgását okozzák. Ez ugyanúgy igaz a forgó tárgyakra, mint az egyenes vonalban mozgó tárgyakra, tehát a szögimpulzus megőrzése ugyanazt az önindukciós alapelvet követi.

A forgó tárgyak mechanikus-mágneses-szerű mezőt hoznak létre, amely nyomásváltozásokhoz vezet, akárcsak a mágnesek az elektromágneses elméletben. A különbség az, hogy az elektromágneses teret létrehozó elektromos áramok sebessége közel van a fénysebességhez, a mechanikai forgás pedig lényegesen lassabb. Ez azt jelenti, hogy a mechanikai-mágneses erők általában meglehetősen kicsik az elektromágneses erőkhöz képest.

Az az elképzelés, hogy a fizika megmagyarázza a mechanikai mozgást, hazugság. Nincs magyarázat arra, hogy a forgó tárgyak, mint például a búgócsigák és a giroszkópok, hogyan befolyásolják a vákuumot. Ha megértjük, hogy léteznie kell egy mechanikus dipólusnak, és a Casimir elméletének megfelelően kölcsönhatásba lép velük, akkor nyilvánvalóvá válik, hogy az érintésmentes mechanikai mozgás az éterben lévő nyomáskülönbségeknek miatt jön létre a kiterjesztett Casimir-erő részeként.

44 A.E. Dolbear, Mozgásmódok; vagy: A fizikai jelenségek mechanikai felfogása Boston, Lee és Shepard (1897)

25. hazugság: A Sötét Energia nem Erő

A fizikában a 25. legnagyobb hazugság az, hogy a sötét energia nem erő. A sötét energia hipotézise beigazolódott, amikor a csillagászok kimutatták, hogy az egyetemes tágulás üteme gyorsul. Három asztrofizikus Nobel-díjat kapott felfedezéséért. 45 Mivel a szabványos modellben nincs erőelmélet a gyorsuló tágulás magyarázatára, a fizikusok felismerték, hogy valami ismeretlen történik, és a sötét energia nevet adták ennek. Ez egy titokzatos energia, amely szétválasztja a galaxisokat az űr legmélyebb részein.

Newton második törvénye, az F = ma szerint a tömegre ható erő felgyorsítja azt. Ennek az ellenkezője is igaz; ha egy tömeg gyorsul, akkor erő hat rá. A sötét energia nem pusztán energia; ez egy hiányzó alapvető erő. Talán jobb lenne sötét erőnek nevezni, és innentől ezt fogom tenni. A fizikusok gyakran beszélnek az energiaegységekben kifejezett erőkről, de ha ezt az erőt sötét energiaként említik, az az igazság szándékos elhomályosítása. A fizikusok hazudnak, és úgy tesznek, mintha ez a hiányzó alapvető erő nem lenne akkora probléma, mint amilyen valójában az.

Ennek a hazugságnak az a sajnálatos következménye, hogy a hiányzó erőprobléma nem kapja meg a megérdemelt figyelmet. A probléma megoldására tett legtöbb próbálkozás a meglévő, megvalósíthatatlan elméletek kijavítása volt. Az új, korábban ismeretlen erőhipotézisek híveit bolondoknak bélyegzik. A standard modell fizikusai úgy döntöttek, hogy a szabványos modellen túli minden erőmodell peremfizika, még ebben az esetben is, amikor a megfigyelések azt mutatják, hogy egy korábban azonosítatlan erő van jelen.

Szerencsére egy olyan erő, amely az anyagot eltaszítja a többi anyagtól, teljesen összhangban van a mechanikai erőelmélettel, amely a mechanikai erőket az elektromágneses erőkhöz hasonló módon magyarázza. Az elektromágneses elméletben, ahogy a töltések taszítanak, úgy hasonló mechanikai erővel, mint az anyagtestek is taszítanak. Ily módon lehetséges, hogy a sötét erő egyszerűen csak egy mechanikai erő. És figyelje meg a fizikusokat: figyelmen kívül fogják hagyni ezt a nyilvánvaló tényt.

Ez azt jelenti, hogy eddig hat alapvető erő létezik. Ezek:

1. mechanikai erő,

2. elektromágneses erő,

3. gyenge erő,

4. erős erő,

5. gravitációs erő,

6. sötét erő.

Ha azt mondjuk, hogy a sötét energia nem erő, az hazugság. A fizikusok soha nem fogják tudni megfejteni a sötét energia rejtélyét, amíg nem kezelik új, alapvető erőként. Hajlandónak kell lenniük a standard modell megnyitására, hogy új erőt adhassanak hozzá, bármivé is váljon ezáltal a modell.

45 Fizikai Nobel-díj 2011.

26. hazugság: A gravitáció alapvető erő

A fizikában a 26. legnagyobb hazugság az, hogy a gravitáció alapvető erő. De ez ne okozzon sokkot, mert az emelletti érvelés egy pillanat alatt világos lesz. Ugyanakkor azt is vegyük figyelembe, hogy ez nem jelenti, hogy a Napot és a Naprendszerünk bolygóit nem valamilyen erő tartaná egyben, mert igen. Csak hát ez nem olyan egyszerű helyzet, mint ahogyan ezt Newton és Einstein elmélete leírja. - OK, talán még mindig sokkal egyszerűbb, mint Einstein elmélete.

Az ok, amiért a jelenlegi gravitációs elméletek nem alapvetőek, az a sötét energia, pontosabban a sötét erő, ahogyan azt az utolsó fejezetben tárgyaltuk. Ahol van gyorsulás, ott van egy erő, F = ma, és jelenleg a standard modellben nincs olyan erő, amely a nagy, elektromosan semleges anyagtestek távolodását okozná egymástól.

Egyrészt megvan a jól ismert gravitációs erő, amely az anyagtesteket egymáshoz vonzza. Ez az erő Naprendszerünkben a legnyilvánvalóbb. Másrészt ma már tudjuk, hogy van olyan erő, amely gyorsuló ütemben taszítja a testeket.

Ezért nem lehet elkerülni azt a következtetést, hogy a newtoni gravitáció és az Einstein-féle általános relativitáselmélet legalább két erő összege. A két különálló és különálló erőből álló erő nem alapvető erő. A két erő, bármi is legyen, az alapvető.

Az egyik ilyen erő felfogható nagyenergiájú gravitációnak, a másik pedig a sötét erőnek. Ez a két erő ellentétes irányban hat, és közel azonos nagyságúak. Vegye figyelembe, hogy ez megmagyarázza a fizika egyik régóta megválaszolatlan kérdését is, hogy a newtoni gravitáció miért ilyen gyenge erő. Valójában ez a különbség két olyan erő között, amelyek önmagukban sokkal erősebbek. Nagyságrendjükben valószínűleg közelebb állnak az elektromágneses erőkhöz, amint azt várnánk, ha az összes erőt egyetlen elméletben egyesíthetnénk.

Szomorú, hogy a gravitációs elmélet ilyen nyilvánvaló problémáját figyelmen kívül hagyták. Nem mintha a világegyetem gyorsuló tágulása ismeretlen lenne a legtöbb fizikus számára, azonban minden kritikai gondolkodásra képes fizikusnak azonnal tisztában kellett volna lennie e korábban fel nem ismert gyorsító erő létezésének következményeivel.

Szerencsére még mindig használhatjuk a newtoni gravitációt számítási célokra, miközben megpróbáljuk megérteni ennek a kétkomponensű erőnek a valódi természetét. Legalábbis a Naprendszer léptékében a mérnöki szintű matematikán nem kell változtatni. A fizika szempontjából a nagyenergiájú gravitációs erőt a newtoni gravitációhoz hasonló módon, de más állandóval írhatjuk le, vagy kiderülhet, hogy valami egészen más, mint amit Newton kitalált. Az általános relativitáselmélet sokkal problematikusabb, és a későbbi fejezetek témája lesz. Egy görbült térmodell nem működik, ha két erőt kell összeadnunk.

A sötét erő természetének kérdése is nyitott. Természetesen, ha a mechanikai erő térerő, ahogy látszik, akkor ez megmagyarázná a sötét erőt is. A tudósok a sötét energia más formáit is figyelembe vették, ami felveti azt az elképzelést, hogy a gravitáció három vagy több erő kombinációja is lehet. Tudósként nyitottnak kell lennünk minden lehetőségre, miközben a legegyszerűbb megoldásokat kell keresnünk.

Még mindig van a fizikusok egy kis csoportja, akik szerint a gyorsulásmérés tévedés. Ez azonban nem tántoríthat el minket a lényegtől, mivel a mechanikai térerő azt jelenti, hogy van olyan erő, amely az egyik anyagot taszítja a másiktól. A mechanikus Lorentz-erő létezése a spirálgalaxisokban azt mutatja, hogy meg kell küzdenünk egy nagy hatótávolságú taszító erővel.

További kérdés, hogy a nagyenergiájú gravitáció mennyire erősebb a naprendszerek és galaxisok skáláján rövidebb távolságokon, és a sötét erő erősebb intergalaktikus távolságokon. Ez egyelőre nyitott kérdés marad, mivel ennek a két erőnek a nullponti mezőn keresztüli átvitelének módjához van köze.

Tehát most módosítanunk kell a gravitáció nélküli alapvető erők listáját. Ezek:

1. mechanikai erő,

2. elektromágneses erő,

3. gyenge erő,

4. erős erő,

5. sötét erő,

6. nagyenergiájú gravitációs erő.

Az az állítás, hogy a gravitáció alapvető erő, hazugság. A sötét erő létezése azt sugallja, hogy a gravitációnak két vagy több erőből álló erőnek kell lennie.

27. hazugság: A sötét energia nem okoz tágulást

A fizikában a 27. legnagyobb hazugság az, hogy a sötét energia nem okoz tágulást. Bár nem biztos, hogy fizikusok kifejezetten kijelentik ezt a hazugságot, mert ez a sötét erő problémájának nyilvánvaló kiterjesztése. A világegyetem kozmológiájáról szóló bármely cikkben a tágulás és a gyorsulás problémáit külön kezelik. Feltételezésük az, hogy a gyorsulás valahogy úgy történik, hogy közben nem változik a tágulás mögötti mechanizmus.

Ahogy az utolsó két fejezetben tárgyaltuk, ha van gyorsulás, akkor van erő. Lehet, hogy ez az erő új számunkra, de nem egészen új. Alapvető erőről beszélünk, tehát mindig minden anyagra hatott, az idők kezdete óta. Ez azt jelenti, hogy nem csak a sötét erő felelős az egyetemes gyorsulásért, hanem felelősnek kell lennie az intergalaktikus tágulás egy részéért vagy egészéért is.

Az az elképzelés tehát, hogy a sötét energia nem okoz tágulást, hazugság. A sötét erő felelős a tágulás felgyorsításáért, és felelős általában a tágulásért, vagy legalábbis annak egy jelentős részéért. A mainstream fizikusok hazudnak maguknak és másoknak, amikor nem veszik figyelembe a sötét erő hozzájárulását az intergalaktikus terjeszkedéshez.

28. hazugság: A nem-tér létezése

A fizika legnagyobb hazugságai közül a 28. a nem-tér létezése. Ha olyan ön, mint a legtöbb ember, valószínűleg soha nem hallott a nem térről, mivel a fizikában nincs rá hivatalos kifejezés. Ez egy olyan típusú tér, amely nem igazán tér. De miért akarna valaki is olyan teret feltalálni, ami „nem-tér”? A válasz erre a kérdésre a hipotetikus ősrobbanás-modellben rejlik.

Az ősrobbanás modell feltalálói azt feltételezték, hogy az ősrobbanás egy ponton nagy energiával indulhat el. Ekkor az energia kitágulna, részecskék képződnének, végül az anyag atomokká, csillagokká és galaxisokká egyesülne. De várjunk csak, ez azt jelentené, hogy az egész univerzum kezdetben egy kicsiny pont volt? És mi volt akkor az univerzumon kívül?

A válasz, amit javasoltak, nem volt, és ez nem csak egy üres hely nem volt, afféle semmi, de még csak nem is tér. Az általános relativitáselmélet kidolgozása során ekkoriban a fizikusok tisztában voltak a téridő fogalmával, de itt megjelent náluk az univerzumon kívüli üres tér, így kezdetben az volt, hogy nincs se tér, se idő az elképzeléseikben. Egyáltalán nem voltak méretei. Természetesen, mivel az univerzumon kívül volt, ez sem kimutatható, sem mérhető nem volt.

Úgy képzelhetitek el ezt, mint egy léggömb felfújását, ahol a léggömb az egész univerzum, azon kívül pedig a tiszta semmi van. Ahogy a léggömb felrobbant és egyre nagyobb lesz, úgy nő az univerzum mérete, de akármekkora lesz is a léggömb, mindig a semmi veszi körül.

Amit ők kitaláltak, a semmi fogalma volt, amit nem nevezhetünk térnek. És persze ebben a nem-térben nem lehetnek vákuum-ingadozások sem. A vákuum-ingadozásoknak hullámhossza és frekvenciája van; térbeli méretekkel és idővel rendelkeznek. Tehát a nem-térnek vákuum-ingadozás és étermentesnek kell lennie. És ennek az éterelutasítók nagyon örültek.

De várj egy percet; ezek az emberek nem fizikusok? A fizikusoknak fizikai és matematikai leírásokat kell készíteniük a fizikailag valóságos dolgokról. A nem-térnek nincsenek méretei vagy ideje, így nem mérhető, és nem fizikai. A nem-tér kívül esik univerzumunkon, tehát nem megfigyelhető, nem észlelhető és nem is mérhető. És még csak nem is ez a baj.

Valójában nem-tért soha nem figyeltek meg az univerzumunkban. Univerzumunkban minden tér valódi tér. Nem csak az, hogy az univerzumunk minden tere vákuum-ingadozásokat tartalmaz, tehát vannak térbeli méretei és ideje. Univerzumunkban minden térben van éter.

Tetézni a nem-űrt nem is szükséges, hiszen enélkül is kidolgozhatunk egy átfogó elméletet. A nem-térhipotézis szükségtelen bonyodalom. Inkább valláshoz, mint tudományoshoz hasonlítható. A nem-tér egy nem tudományos hipotézis, mivel:

1. Nincs rá tárgyi bizonyíték.

2. Az univerzumot felesleges leírni.

3. Felesleges új bonyodalmakat ad hozzá univerzumunk elméleteihez.

4. Soha nem lehet kimutatni.

A nem-tér hazugság. Van egy kifejezés, amely olyasmire vonatkozik, ami nem megfigyelhető, nem észlelhető és nem mérhető. Fikciónak hívják. Vagy ebben az esetben, mivel ezt a tudósok találták ki, ez sci-fi. Nincs olyan valami, hogy „nem-tér”.

29. hazugság: Az ősrobbanás figyelmen kívül hagyhatja a sötét energiát

A fizikában a 29. legnagyobb hazugság az, hogy az ősrobbanás figyelmen kívül hagyhatja a sötét energiát. Sok év telt el azóta, hogy megállapították, hogy az univerzum tágulási üteme felgyorsul, és évekkel ezelőtt kiosztották ezért a munkáért a Nobel-díjat. Időközben az ősrobbanás teoretikusainak nem sikerült az ismeretlen sötét erőt beépíteni az ősrobbanás modelljébe. Vagy talán senki sem volt hajlandó közzétenni ezeket az eredményeket, mert nem kedveznek a modellnek.

A legjobb helyzetben a hipotetikus ősrobbanás-modell nagyon törékeny, mivel finoman kiegyensúlyozott. Az ősrobbanással kapcsolatos egyik finomhangolási probléma az úgynevezett lapossági probléma. A gravitációs elmélet alapján az univerzum sűrűsége pontosan egyensúlyban van a lassú, egyenletes tágulás és az összeomlás között. Az ősrobbanás modell hatókörén belül, ha valamivel több lett volna a tömeg és az energia, akkor az univerzum a gravitáció hatására összeomlott volna, ha pedig valamivel kevesebb lenne a tömeg és az energia, akkor sokkal nagyobb ütemben tágulna. E kényes egyensúly eléréséhez a kezdeti tömegnek és energiának sok tíz nagyságrenddel pontosnak kellett volna lennie. Ez lényegében statisztikailag, következésképpen tudományosan lehetetlen, és a fizikusok mégis ragaszkodnak az ősrobbanás hipotézisének alátámasztásához.

Most hozzá kell adnunk a sötét erőt ehhez a finoman kiegyensúlyozott modellhez, de ha csak egy kis új erőt is megkísérelünk hozzáadni az ősrobbanás egyenletéhez, akkor azok már nem működnek. Ezt minden fizikusnak azonnal fel kellett volna ismernie, ha feltételezi, hogy az erőelmélet alapjaival is rendelkezik. De ehelyett egyszerűen nem vetik fel, abban a reményben, hogy a probléma valahogy elmúlik, és úgy tesznek, mintha a sötét erőnek valahogy nem kellene integrálódnia az ősrobbanás modelljébe.

Valaki megbecsülni a sötét erő nagyságát a gyorsulási sebesség alapján. Aztán beépíthetik ezt a feltételezett sötét erőt az ősrobbanás számításaiba. Ne feledje, hogy a sötét erő nem valami újdonság, hanem olyasvalami, ami minden testre hatott minden idők óta. Tehát ha úgy gondolja, hogy az univerzum 13,7 milliárd éves, akkor a sötét erő 13,7 milliárd éve gyorsítja egymástól a galaxisokat és más anyagokat.

Ez felveti a kérdést: az intergalaktikus sebesség, az univerzális tágulás mekkora része köszönhető a sötét erőnek? A válasz talán 50%, 100% vagy esetleg néhány százaléknál van? De elhagyom inkább a kicsiny becsléseket, és megjósolom: 100%!

Az ősrobbanás elmélete szerint az intergalaktikus tágulás az ősrobbanásnak köszönhető. Az elmélet szerint a kezdeti sebességek nagyon nagyok, és az idő múlásával lelassultak. De mekkora része maradna a feltételezett ősrobbanás miatti tágulásból, ha a számításhoz hozzáadná a sötét erőt is? A válasz 0%.

Az az elképzelés, hogy az ősrobbanás figyelmen kívül hagyhatja a sötét energiát, hazugság. A gyorsuló tágulásért felelős hiányzó alapvető sötét erő szinte biztosan felelős az univerzum jelenlegi tágulási üteméért. Nem lehetett nagy durranás a feltételezett ősrobbanásban.

30. hazugság: Az ősrobbanás meghaladhatja a fénysebességet

A fizikában a 30. legnagyobb hazugság az, hogy az ősrobbanás meghaladhatja a fénysebességet. Az anyagtestek fénysebesség-határértéke a fizika egyik kísérletileg megerősített alapelve. Lehetetlen, hogy bármely anyagi test fénysebességgel mozogjon. A fizikusok mégis úgy tesznek, mintha az ősrobbanás-modell valamilyen módon megsérti a fénysebesség-határt.

A hipotetikus ősrobbanás-modell legegyszerűbb változatában az univerzum szingularitásként, egyetlen térbeli pontként kezdődik, vagy legalábbis valami olyasvalamiként, amely közel áll ahhoz, mint egy végtelenül sűrű energiacsomag. Aztán az ősrobbanás után az újonnan keletkezett anyag kifelé tágul.

De várjunk csak. Amint az összes energia, anyaggal vagy anélkül, felbukkan a semmiből, azonnal fekete lyukat képez. És mint minden más fekete lyuk esetében, az anyag vagy az energia nem tud kilépni a fizikai határain. A fekete lyukban lévő anyag és energia nem tud mozogni. Az anyagnak és az energiának meg kell haladnia a fény sebességét, hogy egyáltalán táguljon.

Ez még nagyobb probléma, mint egyetlen fekete lyuk, mivel a szupersűrű anyag és energia, mint egy neutroncsillag, melyről úgy gondolják, hogy a napunk tömegénél körülbelül háromszor nagyobb fekete lyuk lesz. Ez azt jelenti, hogy az ősrobbanást nagyon kis anyag- és energiadarabokra kell felosztani, jóval a fekete lyuk küszöbértéke alatt.

Az ősrobbanás kezdetére vonatkozó szabványos modellek mindegyike megsérti a fénysebesség-korlátozást a fekete lyukak képződése tekintetében. Tehát hazugság a hazugságban az, hogy a fizikusok úgy gondolják, hogy az univerzum összes energiája nem hoz létre fekete lyukat.

Mellesleg, ha a látható univerzumban lévő becsült tömeg egy helyen lenne, egy fekete lyukat képezne, amelynek eseményhorizontjának sugara kb. 20 milliárd fényév. Ne feledje, hogy a számítás alapja egy alacsony tömegbecslés, tehát sokkal nagyobb is lehet. Vagy a gravitáció nem követi a gravitáció univerzális léptékű elveit, vagy a fekete lyuk belsejének standard modellje borzasztóan rossz, vagy mindkettő. Ha mindkettőre gondolsz, reklamálj a tanáraidnál.

Feltételezve, hogy megsérthetjük a fizika ezen alapelvét, és az anyagot és energiát a fekete lyukon kívülre juttathatjuk, még mindig van egy problémánk. A tágulási sebesség megközelítheti a fénysebességet, de kisebbnek kell lennie. Ahogy aztán kialakulnak a csillagok és galaxisok, fényük fénysebességgel jut át ​​az univerzumon. És hogy egyértelmű legyen, a fény sem mozog gyorsabban a fénysebességnél, bár a sebesség változik az átviteli közeggel.

Ha egy hipotetikus, 13,7 milliárd éves univerzumot tekintünk, amely egy ponttól közel fénysebességgel tágul, akkor 6,85 milliárd év elteltével a világegyetem peremén olyan galaxisok lesznek, amelyek minden irányban fényt bocsátanak ki. Tegyük fel, hogy van egy megfigyelőnk, aki még mindig az eredeti kiindulási pont közelében van, valaki olyan, mint mi, de nem mi, mert nem lehetünk olyan szerencsések, hogy pontosan a középpontban vagyunk. További 6,85 milliárd évre lenne szükség ahhoz, hogy a fény az univerzum pereméről visszajusson a kiindulási pontra. Tehát amikor a megfigyelő egy 6,85 milliárd fényévnyire lévő galaxist lát, a feltételezett ősrobbanás-univerzum már 13,7 milliárd éves.

Természetesen ez a galaxis, ha továbbra is közel fénysebességgel mozogna, most 13,7 milliárd fényévre lenne a kiindulási ponttól, de a kiindulási ponton lévő megfigyelő ezt a fényt további 13,7 milliárd évig nem láthatja, csak amikor a világegyetem már 27,4 milliárd éves.

A csillagászok csaknem számtalan objektumot figyeltek már meg, amelyek 6,85 milliárd fényévnél távolabb vannak a Hubble-skála alapján, ami azt jelenti, hogy a hipotetikus ősrobbanás-modell, amely egy pontszingularitásból indul ki, megsérti a fénysebesség határát. Nemcsak az anyag fénysebesség-határát sérti meg, hanem ahhoz, hogy az univerzum széléhez közeli objektumok most láthatóak legyenek számunkra, a fénysebesség határát is meg kell szegni.

Vegye figyelembe a szingularitástól kezdődő ősrobbanás figyelmeztetését. Egyes fizikusok szerint ennek nem kell szingularitásnak lennie. Ahhoz, hogy a fény 13,7 milliárd fényév távolságból 13,7 milliárd évet utazhasson, egy feltételezett ősrobbanásnak azonnal meg kellett volna töltenie egy legalább 13,7 milliárd fényév sugarú gömböt. Valóban nagyobb kell, mert nem valószínű, hogy középen vagyunk, bár így látszik. Valószínűleg más okból is úgy tűnik, hogy pontosan mi vagyunk a középpontban.

Ha figyelembe vesszük egy ilyen alternatív ősrobbanás modellt, amely azonnal kitölti az ismert látható univerzum térfogatát, ez még mindig nem magyarázza meg a tágulást, legalábbis a sötét erőhöz való visszatérés nélkül. Az más kérdés, hogy egyszerre tölt-e be minden teret; de miért nem gondolunk egyszerűen egy állandó állapotú univerzum modellre? Az anyag valahogy megjelenik. Miért nem foglalkoznak először ezzel a problémával, és megnéznék, hová ez vezet?

Ez a probléma még súlyosabbá válik, ha figyelembe vesszük, hogy az asztrofizikusok azt állítják, hogy a világegyetem átmérője 93 milliárd fényév, vagy talán még nagyobb. 46 Nincs mód arra, hogy az univerzum akkora legyen, hacsak nem ekkora vagy nagyobb volt.

Az az elképzelés, hogy az ősrobbanás-modell meghaladhatja a fénysebesség határértékét, hazugság. Ez a fizika egyik legnagyobb hazugsága. Maga az ősrobbanás-modell követeli meg, hogy az anyag és a fény fénysebesség-határait megszegjék.

46 I. Bars, J. Terning, Extra Dimensions in Space and Time, Springer 27. o., 2009.

31. hazugság: Az inflációs hipotézis

A fizikában a 31. legnagyobb hazugság az inflációs hipotézis. Amint arra a 30. hazugság rámutatott, az ősrobbanás modell megköveteli a fénysebesség-korlátozás megsértését. A Hubble-skála szerint olyan galaxisokat látunk, amelyek több mint 7 milliárd fényévnyire vannak tőlünk. Ahhoz, hogy ez igaz legyen egy pontból induló világegyetemre, az anyagnak gyorsabban kellett volna mozognia, mint a fénysebesség. És ahhoz, hogy a tárgyak 13,7 milliárd fényévnyire legyenek láthatók, a fénynek gyorsabban kell mozognia, mint a fénysebesség. Természetesen mindkét fénysebesség-sértés lehetetlen.

A fizika által ismert talán legnagyobb önbecsapás az, hogy az inflációs hipotézist javasolták, hogy a lehetetlent lehetővé tegyék. 47 Az inflációs hipotézis hívei szerint így a fénysebesség-határérték már biztonságosan áthágható.

Az inflációs hipotézis szerint az univerzum tere egy pillanat alatt kitágul, és az anyag csak normálisan tágult, és soha nem haladt gyorsabban, mint a világűrhöz viszonyított fénysebesség. Tehát nemcsak nem-tér volt az univerzumon kívül, hanem kvázi nem-tér is az univerzumon belül is. És ez a kvázi nem-tér megváltoztathatja a dimenziókat és gyorsan tágulhat. Így az legtéveszmésebb fizikusok azt gondolhatták, hogy a fénysebesség határértékét nem sértették meg.

Ezek a fizikusok természetesen elutasítják a vákuum-ingadozást, vagy már el sem hitték az ilyen ostobaságokat. A valós tér viszont vákuum-ingadozásokat tartalmaz, tehát ahhoz, hogy bármely fizikailag valós tér a fénysebességnél jóval nagyobb ütemben táguljon, elegendő energiának kell lennie ahhoz, hogy az összes vákuum-ingadozást ezen a sebességen kinyomja. Ennek a szuperluminális anyagnak is le kell győznie a vákuum-ingadozások miatti normál mozgási ellenállást. És igen, a tehetetlenség még mindig a mozgással szembeni ellenállás egyik formája.

Ne feledje, hogy egy köbcentiméter vákuumban legalább 1095 gramm anyag energiaegyenértéke van, ami sokkal nagyobb, mint a teljes látható univerzum tömegenergiája az ősrobbanás modellje szerint. Nincs elég energia az egész hipotetikus ősrobbanásban ahhoz, hogy akár egy köbcentiméteres vákuum-ingadozást is kiterjesszen, még kevésbé felfújjon lehetetlen sebességgel.

A mi univerzumunkban nem létezik olyan, hogy kvázi nem-tér, bárminek is nevezzük. Ilyesmit még sohasem figyeltek meg. Bármerre nézünk, mindenhol tér van: van vákuum, és vannak vákuum-ingadozások. Az inflációs hipotézis nem fizika, hanem sci-fi, és így hazugság.

47 A. Guth, The Inflationary Universe: The Quest for a New Theory of Cosmic Origins, Perseus, 1997.

32. hazugság: A kozmikus mikrohullámú háttér az ősrobbanást bizonyítja

…a töltött részecskékkel termikus egyensúlyban lévő sugárzás esetén visszatérhetünk Planck, Einstein és Bose megfontolásaihoz, amelyek minden ν frekvenciára megadják a Planck-képletet a sugárzás intenzitására (anyaggal egyensúlyban). …látni fogjuk, hogy ennek a képletnek milyen óriási jelentősége van a kozmológiában, mivel rendkívül jó összhangban van a kozmikus mikrohullámú háttér sugárzási spektrumával. 48

Roger Penrose, 2016

A fizikában a 32. legnagyobb hazugság a Cosmic Microwave Background (CMB) a kozmikus mikrohullámú háttérsugárzás bizonyítja az ősrobbanást. Íme, ez egy másik nevetséges állítás, amelyről a vákuum-ingadozást elutasítók csak álmodozhatnának. A háttérben két amerikai rádiócsillagász, Arno Penzias és Robert Woodrow Wilson véletlenül fedezte fel a CMB-t 1964-ben, amikor háttérzajt észleltek kürtantennájukban, amely egyenletes volt az égen. 49 Az általuk mért mikrohullámú hullámhossz nagyjából 3 Kelvin (K) hőmérsékletnek felelt meg, amelyet jelenleg 2,7 K-nak fogadnak el. Penziast és Wilsont később Nobel-díjjal tüntették ki ezért a felfedezésükért.

Az az elképzelés, hogy a tér vákuumának hőmérséklete nem nulla, nem volt újdonság. 1896-ban Charles-Edouard Guillaume kiszámította, hogy az űr hőmérséklete 5,6 K a csillagfény-sugárzás miatt. 50 Sir Arthur Eddington hasonló számítást végzett, és 3,18 K hőmérsékletet számított, ami nagyon közel áll a jelenleg mért hőmérséklethez.

Később, az ősrobbanás-modell megalkotása után, több fizikus kiszámította egy feltételezett ősrobbanásból származó maradék hőenergiát, és általában azt találta, hogy az a jelenleg elfogadott hőmérsékletnél körülbelül 10-szer nagyobb hőmérsékleti jelet hagy maga után. Mindazonáltal, miután felfedezték a CMB-t, az ősrobbanás teoretikusai azonnal azt állították, hogy a CMB az ősrobbanás modelljének bizonyítéka. Ezután módosították a becsléseiket, hogy illeszkedjenek az adatokhoz.

A mikrohullámú háttérsugárzás mérése az űrben valójában nagyon keveset árul el arról, hogy mi okozza ezt további információk nélkül. Amint azt korábban említettük, a tudósok képesek voltak észlelni egy Doppler-eltolódást, amely azt jelzi, hogy Naprendszerünk a CMB-hez képest hogyan mozog, ez azt jelenti, hogy az univerzumnak valóban van alapállapota. És mivel fizikailag nem lehetséges, hogy két kiindulási alapállapot legyen, egy az éternek, egy a CMB-nek, ennek kell lennie az éter alapállapotának is.

Vegye figyelembe azt is, hogy csak két dolog, amiről tudjuk, hogy egységes a látható univerzumban: az éter és a CMB. A CMB sugárzásának valamilyen módon az éterből kell származnia. Ahogy Roger Penrose állítja, a CMB eloszlásból származó fekete test sugárzás alakja megegyezik Planck előrejelzésével. A CMB fekete test sugárzást bocsát ki egy étert tartalmazó mechanizmuson keresztül. Az üres tér nem sugározhatna, ha nem lenne tele éterrel. A CMB bizonyítékai igazolják, hogy az éter-alapállapot mellett Planck típusú éter is létezik.

Fontos még megjegyezni, hogy a CMB minden időből és térből származik, hiszen minél távolabbra tekintünk az időben, annál távolabbra tekintünk vissza. A CMB nem csupán egyetlen, réges-régi időpontból származik az univerzum történetében. A múltból származik, és változatlan. Ez azt jelenti, hogy nem történt olyan jelentős változás az alapvető állandókban, amelyek idővel megváltoztathatnák a CMB feketetest-spektrumát. Bármi okozza is a CMB-t, az egy állandó folyamat.

Ezen túlmenően csak azt mondhatjuk, hogy kell lennie egy mögöttes folyamatnak, amely a CMB-hez vezető háttérhőmérsékletet okozza. Ennek a hőmérsékletnek a forrását még nem azonosították be teljes bizonyossággal.

A korai első modellekkel a probléma kettős; a csillagok nem egyenletesen oszlanak el az univerzumban, és a vákuum ingadozása nem nyeli el a fotonokat. Egymilliárd fényév átmérőjű üregek vannak. A csillagok hője és fénye nem egyenletes, így hacsak a hő nem terjed az éteren a fénysebességnél sokkal gyorsabban, a CMB nem a fénynek köszönhető. Szükségünk lenne egy fizikai mechanizmusra is, amely leírja, hogyan lépnek kölcsönhatásba a fotonok a vákuum-ingadozásokkal, amely felmelegíti őket, majd szükségünk van egy olyan mechanizmusra, amely felszabadítja a fekete test spektrumú fotonokat. Nekünk nincs egy sem a standard modellünkben.

Általában úgy gondoljuk, hogy az éternek, amely betartja a Planck- és Heisenberg-határokat, nem lenne érzékelhető nulla feletti hőmérséklete, mivel minden vákuum-ingadozás nulla energiájúvá válik. De lehet, hogy újra meg kell vizsgálnunk ezt a feltételezést. A gáz hőmérséklete a gázmolekulák kinetikus energiájának függvénye. Talán a vákuum van der Waals energiája látszólagos hőmérsékletet ad a van der Waals által indukált mozgás miatt. Aztán amikor a vákuum ingadozása időnként megsemmisül, ez a van der Waals hőmérséklet kisugározhat, és fekete test spektrumot bocsát ki. Egy ilyen fizikai mechanizmus, ha megfelelő effektív hőmérséklettel rendelkezik, megmagyarázná a CMB-t.

Alternatív megoldásként tudjuk, hogy az anyag létezik, tehát azt is tudjuk, hogy valamilyen módon elő kell állítani. És tudjuk, hogy az ősrobbanás-modell valójában nem magyarázza meg az antianyag nélküli anyag előállításának folyamatát. Valójában ez egy másik, az ősrobbanás modelljében rejtett hazugság, hogy ez megmagyarázza az anyag keletkezését.

Az anyagtermelés mögött meghúzódó fizikai mechanizmus, bármi legyen is az, lehet az oka a túlmelegedésnek. A CMB-sugárzás ekkor abból az anyagból származó sugárzás lenne, a hőmérséklete miatt. Ha ez a helyzet, a CMB egységessége az univerzumban előforduló, térben és időben is egységes anyagtermelési folyamatnak kedvez, nem pedig egy egyszeri ősrobbanás-típusú eseményhez.

Az az állítás, hogy a CMB bizonyítja az ősrobbanást, hazugság. A CMB valamilyen termikus folyamat bizonyítéka, esetleg nullponti energia- vagy anyagtermelés, talán esélye van a külső fényelnyelési jelenségnek is. Ezek semmiképpen sem csak a képzeleten alapulnak, mint az ősrobbanási modell bizonyítékai. A CMB azonban a Planck típusú éter és az éteralapállapot bizonyítéka.

48 R. Penrose, Fashion Faith and Fantasy in the New Physics of the Universe, 195. oldal, Princeton University Press, 2016

49 A.A. Penzis, R.W. Wilson, „A Measurement of Antenna hőmérséklet 4080 Mc/s”, Astrophysical Journal, Vol. 142 pp.419-421, 1965.

50 Guillaume, Charles-Edouard (1896). "La Température de L'Espace (A tér hőmérséklete)". La Nature. 24.

51 Eddington, A. 1926, 371-372. A csillagok belső felépítése. Cambridge, Cambridge, Egyesült Királyság: Cambridge University Press.

33. hazugság: Az ősrobbanás megsértheti az energia-megőrzést

A fizikában a 33. legnagyobb hazugság az, hogy az ősrobbanás megsértheti az energia-megmaradás törvényét. Bárki, aki csak egy kicsit is tanult fizikát, tudja, hogy az energia-megmaradás a fizika legfontosabb alapelvei között szerepel. Az energia nem keletkezik és nem is semmisül meg, az energia csak egyik energiafajtából a másikba alakulhat át. A leghíresebb transzformáció talán a tömeg energiává alakítása az E = mc2 képlet szerint.

Sokkal gyakoribbak a kémiai energiát, hőenergiát, mechanikai energiát, elektromos energiát és atomenergiát tartalmazó átalakítások. Az olyan energia, mint a vegyi és a nukleáris energia tárolható, majd később hőtermelés céljából felszabadítható. Az elektromos üzemekben a hő fel tudja melegíteni a gőzt, a gőz kitágulása pedig mechanikai energiává, majd elektromos energiává alakítható. Az energiaátalakítás egyik vagy olyan formája gyakori, és megtalálható a legtöbb naponta üzemeltetett készülékünkben.

Az egyetlen dolog, amit azonban nem tehetünk, az az, hogy energiát állítunk elő a semmiből. Csak olyan energiát tudunk kinyerni, amely már jelen van. Az energia raktározódhat atommagokban, vagy atomok és molekulák közötti kémiai kötésekben. Az atomok közötti elektromos potenciálkülönbségek, vagy a vezető vagy félvezető rétegek közötti elektromos mezők hatására energiát tárolhatunk és nyerhetünk ki. Az energia minden esetben már el van tárolva, vagy más energiaforrásból kell hozzáadnunk egy rendszerhez a későbbi visszanyeréshez.

Az ősrobbanás-modellről azt mondják, hogy egy egyediséggel, vagy esetleg egy nagyobb léptékű azonnali eseménnyel kezdődik. Az ősrobbanás modelljében az univerzum összes energiája egy pillanat alatt előkerül a semmiből. Ez a semmi különleges fajtája. Ez nem egy normál térvákuum, amely vákuum-ingadozásokat és nullapont energiát tartalmaz. Az ősrobbanás teoretikusai azt mondják, hogy az ősrobbanás előtt létezett egyfajta tértől eltérő tér, egy tér vákuum-ingadozások, dimenziók, idő és energia nélkül. Emlékezhetsz ezzel kapcsolatban a nem-térre a 28. hazugságból.

Az ősrobbanás teoretikusai úgy vélik, hogy a semmiből kihozhatnak valamit. Úgy gondolják, hogy az energia varázslatosan megjelenhet, ahol korábban nem volt energia. Ez az energia-megmaradás megsértése igazi univerzális léptékben. Sok fizikus, akinek önámítási képessége korlátlannak tűnik, egyszerűen figyelmen kívül hagyja ezt a problémát.

Az ősrobbanás teoretikusai úgy vélik, hogy a semmiből kihozhatnak valamit. Úgy gondolják, hogy az energia varázslatosan megjelenhet, ahol korábban nem volt energia. Ez az energia-megmaradás megsértése valóban univerzális léptékben. Sok fizikus, akinek önámítási képessége korlátlannak tűnik, egyszerűen figyelmen kívül hagyja ezt a problémát.

Az ok, amiért az ősrobbanás teoretikusai úgy érzik, hogy figyelmen kívül hagyhatják az energia-megmaradás megsértését, arra vezethető vissza, hogy a legtöbben a vákuum-ingadozásokat is elutasítják. Ha nincs vákuum-ingadozás, nincs nullaponti energia, tehát a térről alkotott elképzelésüknek nincs energiája. Ez arra készteti őket, hogy azt gondolják, hogy mivel az anyagnak a semmiből kell származnia, legyen az ősrobbanás vagy más modell, akkor rendben kell lennie, hogy anyagot és energiát nyerjünk a semmiből. De ez nincs rendben.

Ha a 19. hazugságból felidézzük azt a feltételezést, hogy a tömeg egy belső tulajdonság, akkor az elektron, a proton és a neutron tömege megegyezik az általuk kiszorított nullponti energia mennyiségével. Ez egyben azt is jelenti, hogy a közönséges anyag létezése nem változtatja meg a térben lévő energia teljes mennyiségét. Ha a tér csak vákuum-ingadozásokat tartalmaz, akkor egy mennyiségű energiája van. Ha bevezetünk egy elektront, akkor is ugyanannyi energiája van. Az anyag nem létezhet vákuumenergia nélkül, és az anyag létezése nem változtatja meg az energia mennyiségét a térben.

Hazugság azt állítani, hogy az ősrobbanás-modell sértheti az energia-megmaradás elvét. A fizika megköveteli, hogy ne sértsék meg az energia-megmaradás elvét, és az ősrobbanás-modell az energia-megmaradás lehető legnagyobb megsértése. Szerencsére ismerjük az univerzumban található összes tömegenergia mögött az energiaforrást. Ez a nullpont energia, és ez volt itt először.

Vegye figyelembe, hogy ez elvezet bennünket a hazugság tágabb változatához. Minden olyan kozmológiai modell, amely nem feltételezi, hogy éterrel töltött tér a végtelenségig létezett, sérti az energia-megmaradás elvét, ezért hazugság.

34. hazugság: Az ősrobbanás

Soha nem gondoltam volna, hogy a gravitáció által uralt ősrobbanás sima, homogén univerzumából megszerezheti azt a rendkívül rögös, heterogén univerzumot, amely ma van, és amelyet erősen befolyásolnak a plazmafolyamatok. 52

Hannes Alfvén

A fizika legnagyobb hazugságai közül a 34. az ősrobbanás. A könyvben található utolsó néhány fizikai hazugság alapján nyilvánvalóvá kell tenni, hogy az ősrobbanás egy nagy hazugság. Egy egész könyvet lehetne írni, és sokat írtak már arról a sok hazugságról, amit az ősrobbanás hazugságának elfedésére gyártottak. Több tucat jó oka van annak, hogy miért nem működik a modell. Íme néhány:

1. Sérti az energia-megmaradás elvét.

2. A sci-fi nem-tér-fogalom.

3. A fekete lyuk probléma.

4. A fénysebesség-korlátozás megsértése.

5. A nagy méret, 1093 milliárd fényév problémája.

6. A nevetséges inflációs elmélet.

7. A sötét erő létezése.

A Hubble-teleszkóp megfigyelési adatokat is szolgáltatott számunkra erősen vöröseltolódású galaxisokról, galaktikus halmazokról és szuperhalmazokról. Nagyon távoli objektumokat látunk, amelyek nem fiatalok, de gyakran nagyon öregek, körülbelül 10 milliárd évesek vagy még ennél is idősebbek. Aztán a Hubble-skála alapján ezek az objektumok 10 milliárd plusz fényévnyire vannak tőlünk. Csak ezek a megfigyelések alapján az univerzumnak több, mint 20 milliárd évesnek kell lennie.

Tehát még ha azt hiszik is, hogy az anyag gyorsabban mozgott a fénysebességnél a korai univerzumban, ezek az objektumok még mindig idősebbek, mint a feltételezett ősrobbanás 13,7 milliárd éves kora. Az ezekről a megfigyelésekről számoló leírások furcsa módon vitatják az ősrobbanást, miközben nem vitatják meg, mivel a mainstream szakfolyóiratok nem teszik lehetővé a fizikusok számára, hogy nyíltan megtámadják az ősrobbanás modelljét.

Vannak olyan üregek és falak is, amelyek kialakulása sokkal tovább tart. A környező csillagok megfigyelései alapján körülbelül egymilliárd fényév átmérőjű üreg van, ahol nem láthatók galaxisok. Ha a galaxisok egyszer elfoglalták a térnek azt a régióját, és névleges, de gyors, mondjuk 1000 kilométer/másodperces intergalaktikus sebességgel távolodtak el egymástól, akkor több száz milliárd évbe telt volna az űr kialakulása. Egy lassan fejlődő, állandósult állapotú modellben az univerzumnak több, mint 1000 milliárd évesnek kell lennie, és ez a modell sokkal jobban illeszkedik a megfigyeléshez, mint az ősrobbanás.

Számos könyv, újság és internetes oldal tárgyalja az ősrobbanás modelljébe ágyazott számos hazugságot. Kérjük, bátran kutasson tovább. Minden tudományosan gondolkodó, racionális gondolkodásra képes ember, aki tanulmányozza az ősrobbanás modell hibáit, arra a következtetésre jut, hogy az ősrobbanás modell hazugság.

52 Idézi Anthony L. Peratt, „Dean of the Plasma Dissidents”, Washington Times, melléklet: The World and I (1988. május), 196.

35. hazugság: Ciklikus univerzum

A fizikában a 35. legnagyobb hazugság a ciklikus univerzum. A ciklikus univerzum modell az ősrobbanás modell következményeként jött létre. Történelmileg az ősrobbanás-modell ugyanazt akarja kifejezni e tekintetben, hogy az univerzum örökké tágul-e vagy visszafordul és összeomlik. Az összeomló univerzumot néha nagy reccsnek is nevezik.

Ez a lapossági probléma, és ez a korábban tárgyalt finomhangolási probléma az ősrobbanás modellnél. Ha valamivel több lett volna a tömeg, az univerzum már rég összeomlott volna. Ha valamivel kevesebb lenne a tömeg, az univerzum már sokkal gyorsabban tágulna, és nem lenne remény arra, hogy valaha is összeomlik. A tömeg és a gravitáció közötti egyensúlyozásnak nevetségesen sok számú tizedes jegyig tökéletesnek kellett lennie. Természetesen ilyen pontos eredmény fizikailag lehetetlen.

Mindenesetre az egyik lehetőség az volt, hogy az univerzum végül összeomlik, nyilvánvalóvá vált, hogy a minta hipotetikusan megismétlődhet, ha hajlandó figyelmen kívül hagyni a fizika néhány alapelvét. Elképzelhető, hogy végtelen számú ősrobbanás következhet be, amit a kiterjedés és az összeomlás időszakai követnek, és ugyanennyi nagy durranás következik be. Ezt gyakran ciklikus univerzum modellnek nevezik. A ciklikus univerzum-modell előnye az egyetlen ősrobbanás-modellhez képest, hogy az egyik ősrobbanás-univerzumból származó energia hozzájárulhat a következőhöz, így megoldja az energia-megmaradás problémáját, ha feltételezzük, hogy ez a folyamat örökké tart.

Miután tudományos bizonyítékok támasztották alá az univerzum gyorsuló tágulását, az összeomló univerzum modelljét a ciklikus univerzum modellel együtt érvénytelenítették. Ha az univerzum tágulási üteme gyorsul, lehetetlen, hogy összedőljön. Ennek ellenére sok évvel később is találhatunk utalásokat egy összeomló univerzumra vagy ciklikus univerzumra.

Mint sok mindennél, az ősrobbanással kapcsolatos dolognál is a hazugság ennél sokkal rosszabb. Ha úgy vesszük, hogy az összeroppanásnál az anyag összeolvad, fekete lyukat képez, akkor ez az anyag és energia nem lesz képes átlépni az eseményhorizontot, mivel ez örökké tartana, ami örökkévalóságban végtelen sok időt jelent. A nagy összeroppanás fogalma hazugság. Amint ez a fekete lyuk kialakul, nem lesz olyan mechanizmus, ami lehetővé tenné, hogy ismét ősrobbanássá váljon, mivel az anyag és az energia örökre a fekete lyuk eseményhorizontjában ragad.

Természetesen az ősrobbanás modell hazugság, amit a ciklikus univerzum-modellt még rosszabb hazugsággá teszi. Ahhoz, hogy a ciklikus univerzum igaz legyen, az univerzum-modellnek egy bizonyos típusú ősrobbanás-modellnek kell lennie, amely egy szingularitásból vagy másképpen térbeli és időbeli pontból indul ki. Amint azt korábban tárgyaltuk, egy ilyen ősrobbanás-modell megsérti a fénysebesség határait a fekete lyukak, az anyagtestek és a fény esetében, emellett számos egyéb problémája is van.

36. hazugság: A gravitáció sebessége a fény sebessége

A fizikában a 36. legnagyobb hazugság, hogy a gravitáció sebessége a fénysebességgel hat. Íme egy újabb hazugság, amit a vákuum-ingadozás elutasítói hoztak nekünk. Először is tagadják a vákuum-ingadozások létezését, és a fénysebességet a fény belső tulajdonságává teszik, nem pedig a fotonok és a nullponti mező közötti kölcsönhatások eredményeként. Innentől kezdve úgy döntöttek, hogy mindennek a maximális sebessége az alapértelmezés szerinti fénysebesség.

Newton korától egészen a 20. század elejéig jól ismert volt, hogy a gravitációs erő átviteli sebességének pillanatnyinak vagy csaknem annak kell lennie, különben az általunk látott bolygópályák instabilok lennének. Ha viszont a gravitáció sebessége a fény sebessége lenne, akkor az erőhatás vételekor a testek elmozdulnának, ami olyan erőket eredményezne, amelyek nem irányulnak az egyes testek aktuális helyzetére. Ezt egyszerűen szemlélteti az alábbi rajz, ahol egy test A pozícióban van az erő hatásakor, de a B helyzetben van, amikor azt kapja, így a testet rossz irányba vonzzák.

36-1. ábra Egy csillag van középen, és bolygó körülte kering. A nyilak azt mutatják, hogy ha a gravitációs erő nem pillanatnyi, akkor nem a másik test felé irányul.

Csillagászati megfigyelések igazolják, hogy a Földet érő gravitációs erő nem a Nap helyzetére irányul a látott fény alapján, ami természetesen késik. A gravitációs erő a Nap tényleges helyzetére irányul. 53

A gravitációs sebesség ezen végzetes hibájának a következménye az a megállapítás, hogy az a fénysebességgel lenne egyenlő, így a pályán keringő bolygók fokozatosan egyre távolabb kerülnének. Elliptikus pályák esetén jelentős további precesszió is előfordulhat, mivel a testek távolabb kerülnek egymástól. A lassú gravitációs rendszerben nem létezhetnek stabil pályák. Tom van Flandern jó elemzést végzett, amikor kiszámolta, hogy a gravitáció sebességének legalább 2 x 1010-szeresnek kell lennie a fény sebességének. 53 De valószínűleg sok nagyságrenddel gyorsabb ennél.

A mainstream fizikusok számos önbecsapó módszert találtak ki a probléma elmagyarázására. Egy ívelt térmodellben azt mondják, hogy a testek a tér geometriai görbületét követik, és nincs valódi erőátvitel. Azt mondják, ez nem más, mint az egymás mellett párhuzamosan mozgó testek.

Aztán azt kérdezed, honnan tudta a tér, hogy merre kell görbülni, azt mondják, hogy minden tér azonnal tudja, hogy hol van az anyag a világegyetem minden részében. Felfogtad? A pillanatnyi ebben az esetben azt jelenti, hogy az információt sokkal gyorsabban kell továbbítani, mint a fénysebesség, így elméletük szerint a gravitáció egyébként is sokkal gyorsabb, mint a fénysebesség. Hazugságaikat sokféle módon újrafogalmazták önmaguk és mások megtévesztésére, de ha elég közelről megnézzük, azt találjuk, hogy megpróbálják elrejteni azt a részt, ahol az erő vagy az erőről szóló információ gyorsabban sugárzott, mint a fény.

Azok a fizikusok, akik elhiszik ezt az ostobaságot, azt is állítják majd, hogy kísérleti bizonyítékaik vannak az alapvető bizonyítékok megcáfolására, miszerint a gravitáció sebessége azonnali. Ha valaki tanulmányozza ezeket az úgynevezett bizonyítékokat, rájön, hogy a kísérletek valójában a fénysebességet mérik. És jellemzően egyáltalán nem a gravitációt mérik, hanem a mechanikai erő egyik összetevőjét.

Ekkor figyelembe kell vennünk, hogy a newtoni gravitáció és az általános relativitáselmélet két ellentétes erő összege kell, hogy legyen, a testeket egymáshoz szorító erő, a nagyenergiájú gravitáció és az univerzum tágulásának gyorsításáért felelős testeket széttoló erő, a sötét erő. A nagyenergiájú gravitációt és a sötét erőt is a fénysebességnél sokkal nagyobb sebességgel kell továbbítani ahhoz, hogy stabil keringési pályák jöjjenek létre. Ha mindkét erő fénysebességgel terjedne, akkor tényleg nem lenne olyan, hogy stabil pálya.

Az az állítás, hogy a gravitáció sebessége a fény sebessége, hazugság. Ez szintén egy újabb hazugság, amit az éterelutasítók hoztak el nekünk.

53 T. van Flandern, „The Speed of Gravity – What the Experiments Say”, Meta Research, Physics Letters A, 250:1-11, 1998.

37. hazugság: Az elektromágneses mezők sebessége végtelen

A fizikában a 37. legnagyobb hazugság az elektromágneses terek sebessége végtelen. Bár a mainstream fizikusok most tömegesen tiltakoznak ez ellen, és tagadják ezt. És teljesen igazuk van: ezt az állítást soha, egyetlen tankönyvben sem találjuk meg. Ha bármit is mondanak az elektromágneses terek terjedési sebességéről, az a fénysebesség.

Az a gondolat, hogy az elektromágneses terek sebessége végtelen, benne van a fizikusok feltevéseiben és egyenleteiben, még akkor is, ha nincs kijelentve. Mint sok más nagy hazugságuk, ez is a vákuum-ingadozás elutasítóinak köszönhető. Mivel nem voltak hajlandók elfogadni a nullponti energia bizonyítékát, amely a fotonátvitel közege, ezért az elektromos és mágneses mezőt a foton belső tulajdonságává kellett tenniük, a fénysebességgel együtt.

Az intrinsic (belső tulajdonság) szónak figyelmeztetnie kellett volna őket, hogy nagy hibát követnek el, egy újabb hazugság a hazugságon belül. A fizikusok egyrészt ragaszkodnak ahhoz, hogy az elektromágneses terek fénysebességgel terjedjenek, másrészt pedig azt állítják, hogy a terjedési sebesség végtelen, de csak belső tulajdonságként. Ez hasonló a gravitációs erőátvitelhez. A Newton-féle gravitációs egyenlethez hasonlóan az elektromosságra és a mágnesességre vonatkozó Maxwell-egyenletek azt feltételezik, hogy az erőátvitel pillanatnyi, vagy majdnem az.

Szemléltetésképpen vegyük figyelembe, hogy amikor egy foton keletkezik, annak egymásra merőleges elektromos és mágneses mezője van. Ezek a mezők a foton hullámfrontjának részét képezik. Mivel a foton minden fél hullámhosszon új pontból származik, az elektromágneses mezőknek végtelen sebességgel kell terjedniük ahhoz, hogy észlelhetők legyenek. Ha nem, akkor nem lennének kimutathatók fél hullámhosszon túl.

Ha egy foton elektromos és mágneses tere csak fénysebességgel terjedne kifelé a központi dipólustól, a mezők nem lennének kimutathatók az egyes dipólusok fénykúpján kívül. Az elektromágneses tér nem tudja előre, hogy a foton mikor nyelődik el.

37-1. ábra Egy foton elnyelődik egy felületen. Ha az elektromágneses tér terjedésének fénysebesség-korlátja van, akkor csak a fénykúpon belüli és az utolsó dipólus melletti térenergiát lehetne elnyelni.

Amikor egy foton elnyelődik, mondjuk egy milliárd fényév megtétele után, csak a központi dipólus energiája nyelődik el. Ez az energia csak a foton fél-hullámhosszán belüli tartományból származna. A fénysebesség határértéke alatt az elektromágneses tér többi része elveszne, és az éterbe vagy a közeli anyagba kellene elnyelődnie.

Honnan tudják a mezők, hogy meg kell szűnniük? A mezők terjedésének feltételezett fénysebesség-korlátja alapján a foton-dipólus és a kiterjesztett mezők közötti kommunikáció lehetetlen lenne. Ahhoz, hogy az elektromágneses mezők a megfelelő pillanatban összeomoljanak, összegyűjtve a foton teljes energiáját, ezeknek a tereknek a terjedési sebességének végtelennek kell lennie. Ez az az implicit feltevés, amelyet az ember akkor tesz, ha korábban átvette a foton standard modellnézetét.

Mivel léteznek vákuum-ingadozások, ezek a dipólusok polarizációjuk és forgásuk révén alkotják az elektromos és mágneses teret. Ezek a mezők dipólusról dipólusra terjednek a térben. Fizikailag lehetetlen, hogy ez a terjedés végtelen sebességgel történjen, pedig rendkívül gyors.

Ezért hazugság az elektromágneses terek végtelen terjedési sebességének implicit feltételezése. Része annak a hazugságnak, hogy az elektromos és mágneses mezők a fotonok belső tulajdonságai.

38. hazugság: Az elektromágneses mezők fénysebességgel terjednek

A fizika legnagyobb hazugságai közül a 38. az elektromágneses terek fénysebességgel terjednek. Az utolsó fejezet után ez a hazugság elég nyilvánvaló. Szokás szerint ezért a hazugságért a vákuum-ingadozást figyelmen kívül hagyók a felelősek. És ez a hazugság ismét abból a téves feltételezésből indult ki, hogy az elektromos és mágneses mezők és a fénysebesség a fotonokra jellemző tulajdonság, nem pedig a vákuum-fluktuációra, a foton-átvivő közeggel való kölcsönhatásra.

Az a feltételezés, hogy az elektromos és mágneses mezők fénysebességgel mozognak, könnyen megcáfolható. Az első esetben ugyanaz a probléma van, mint a gravitációval, ahogyan azt a 36. hazugság kifejti. A Maxwell-egyenletek, mint ahogy a Newton-féle gravitáció is, valójában egy olyan implicit feltételezést tartalmaznak, hogy az erők azonnal terjednek, és a Maxwell-egyenletek kiváló előrejelzéseket adnak a töltések részecskéinek elektromos és mágneses mezőiben történő görbületi pályáiról. Ha az erők csak fénysebességgel haladnának, akkor ezek a pályák eltérőek lennének. Az erő információvétele után az információt továbbító objektum egy másik helyen lesz, ami miatt az erők más irányban hatnak.

Ha ez önmagában nem meggyőző, segíthet egy egyszerű elemzés arról, hogyan terjednek fizikailag a mezők az éteren keresztül. Mint tudjuk, a Casimir-effektusnak köszönhetően léteznek vákuum-fluktuációs dipólusok. Dipólusként polarizálhatók és a mozgó töltésekre reagálva foroghatnak, és van der Waals erőket és nyomatékokat hoznak létre. Mikor a vákuumfluktuációs dipólusok polarizálódnak, elektromos mezőt hoznak létre, forgásukkor pedig mágneses teret. Mindkét mező dipólusról dipólusra terjed a térben.

Tömeg-energia-ekvivalencia alapján 1095 gramm vákuumenergia jut köbcentiméterenként, ami ~1094-szer több energia, mint a Földön található tipikus anyag.

Ez azt jelenti, hogy a töltések aránya hasonló, tehát a mi szempontunkból a vákuumnak csaknem végtelen számú töltése van, és csaknem végtelen kapacitása van elektromos és mágneses terek kialakítására. Mindegyik dipólus 180 fokkal el tud forogni fénysebességgel, de a vákuumfluktuációs dipóloknak csak egy kis töredékére van szükség ahhoz, hogy elektromos vagy mágneses teret hozzon létre.

Ennél is fontosabb, hogy a vákuum-ingadozásoknak nem kell teljes 180 fokkal elfordulniuk ahhoz, hogy elektromos vagy mágneses tér létezzen és terjedjen; csak a fok töredékét kell elforgatniuk. Ha 180 fokkal el kellene forgatniuk egy mező létrehozásához, akkor a mezők fénysebességgel terjednének, de mivel a mezők ennyi forgás nélkül terjednek, sokkal gyorsabban terjednek, mint a fénysebesség. Még az 1/1010 fokos elforgatás is sokkal erősebb elektromos vagy mágneses teret hoz létre, mint bármi, amit létrehozhatunk. A mezők a fénysebesség több mint 1010-szeresével terjedhetnek és terjednek is az éteren keresztül.

Milyen gyors a terjedési sebesség? Ezt nehéz megmondani. Tekintettel az anyag energiája és a vákuum energiája közötti nagy eltérésekre, az elektromágneses mezők a fénysebesség 1094-szeresével vagy gyorsabban terjedhetnek. Vegyük észre, hogy bár jelenleg nem tudunk ilyen kis különbséget mérni a végtelen sebességhez képest, az mégsem végtelen.

Hazugság az a feltételezés, hogy az elektromos és a mágneses terek terjedési sebessége a fény sebessége. Az étert kitöltő dipólusok lehetővé teszik, hogy ezek a mezők sokkal gyorsabban terjedjenek, mint a fénysebesség.

39. hazugság: A horizont probléma

A fizika legnagyobb hazugságai közül a 39. a horizont probléma. A horizont problémát néha homogenitási problémának is nevezik. Ez azért van így, mert a CMB és más jelenségek egységesek az egész látható univerzumban; amikor a feltételezett fénysebesség-korlát miatt az univerzum egyes részeinek nem volt idejük érintkezni egymással egy ősrobbanás típusú modellben. E feltételezett sebességkorlátozás mellett ez a probléma minden olyan kozmológiai modellnél előfordulna, amely egy nem végtelenül ősi univerzumot feltételez.

A 32-es hazugságban megemlítették, hogy az éter termikus egyenletessége, amint azt a mért CMB-sugárzás is mutatja, azt jelzi, hogy a hő, bármi is okozza a CMB-t, a fénysebességnél sokkal gyorsabban átadható. Az utolsó fejezet elmondja, hogy az elektromágneses terek sokkal gyorsabban terjednek, mint a fénysebesség, tehát a van der Waals-erők is sokkal gyorsabban terjednek, mint a fénysebesség. A vákuum-dipólusok remegése a van der Waals-erők hatására áll a legközelebb az éter által generált klasszikus hőhöz.

Ez azt sugallja, hogy a hő a fénysebességnél sokkal gyorsabban átadható. A Van der Waals erők nem a 180 fokkal elforduló vákuum-dipólusoktól függenek, mint a fotonoknál. A CMB termikus tulajdonságai, akárcsak az erők, sokkal gyorsabban terjedhetnek át az éteren, mint a fényé. A CMB és az univerzum egyéb tulajdonságainak egységessége nem meglepő, függetlenül attól, hogy mi okozza a CMB-t.

A horizont probléma hazugság. De az univerzum még így is végtelenül régi lehet.

40. hazugság: Az általános relativitáselmélet megmagyarázza a gravitációs gyorsulást

A fizikában a 40. legnagyobb hazugság az, hogy az általános relativitáselmélet megmagyarázza a gravitációs gyorsulást. Az általános relativitáselmélet modellje a vákuum-ingadozások elutasítása és a mechanika alapjául szolgáló alapvető térerő felfedezésének elmulasztása miatt alakult ki. Ezeknek a helytelen feltételezéseknek köszönhetően az általános relativitáselméletnek számos hibája van, amelyek közül az egyik legnagyobb az, hogy valójában nem magyarázza meg a gravitációs gyorsulásért felelős mechanizmust.

Ennek a figyelmen kívül hagyásnak a feltárásához nem kell mást tennünk, mint egy kéttestes problémát megvizsgálni, ahol két test egymással szomszédos térben van, de kezdetben nem mozog egymáshoz képest. Az általános relativitáselmélet leírja, hogy van köztük egy út, amelyet követni fognak. Relatív tangenciális sebesség vagy más közeli testek nélkül ez az út egyenes vonal a két test között, nem pedig valamiféle pálya.

Az általános relativitáselmélet azonban nem azt mutatja meg, hogyan vonzódnak a testek egymáshoz, így azok egymás felé gyorsulnak. Mint ilyen, az általános relativitáselméletben a két test a végtelenségig ott marad, ahol volt. Még ha vannak is a közelben más testek, az általános relativitáselmélet nem mondja meg, hogy ezek a további testek hogyan gyorsulnak fel, vagy hogyan nyomják az első kettőt. Ha egy hipotézis még egy egyszerű kéttest problémát sem magyaráz meg, akkor nem érdemli meg, hogy elméletnek nevezzük. A gravitációs teoretikusoknak abba kell hagyniuk a számításokat, és meg kell találniuk a fizikai magyarázatot.

Fontos megjegyezni, hogy a newtoni gravitáció sem árulja el, hogy honnan jön a gyorsulás, tehát nincs úgy, hogy vissza tudunk térni egy régebbi modellhez. A Newton-egyenletek elegendőek a naprendszeren belüli gyorsulás eredményeinek meghatározásához, de nem arra, hogy a gyorsulás hogyan történik.

Ezt a problémát jelentősen súlyosbítja az is, ha megjegyezzük, hogy úgy tűnik, hogy a testeket taszító erő is létezik, amellett, hogy vonzza őket. A newtoni gravitációnak vagy az általános relativitáselméletnek meg kell magyaráznia, hogy mindkét erő hogyan vonzza-taszítja a testeket ahhoz, hogy ezek a modellek sikeresek legyenek. Ezt a két erőt egyetlen modellbe kell integrálni.

Amikor azt nézzük, honnan jön a gravitációs hatás, az egyetlen dolog a térben a vákuum, és az egyetlen jelentős dolog a vákuumban a vákuum ingadozása. Mint ilyen, a nyomásnak a vákuum-ingadozások közötti kölcsönhatások miatti nyomásból kell származnia. Ez visszavezet minket a Casimir-effektushoz. Az egyik vagy másik irányú gyorsulás a vákuum nyomáskülönbségeinek köszönhető.

Kiderült, hogy nem is Casimir volt az első, aki ezt javasolta. Az első egy fiatal svájci tudós volt, Nicolas Fatio de Duillier, Newton kortársa. 54 Ő alkotta meg a gravitációs hatás elméletét, amelyet a gravitáció árnyékelméletének is neveznek. Ezt az elméletet később Georges-Louis Le Sage népszerűsítette, és gyakran Le Sage gravitációs elméleteként emlegetik. Le Sage jól ismerte Fatio munkáját, de azt nem igazán fogadta el.

40-1. ábra Az árnyék szemléltetése az elmélet árnyékgravitációs részéből.

Fatio ötlete az volt, hogy az űr tele van testecskékkel, és ahogy ezek a testek az űrben haladnak, véletlenszerűen ütköznek egymással és csillagászati testekkel, lökve őket. Ha két testet tekintünk, az első test az első test mögül érkező korpuszkuláris nyomási erőtől beárnyékolja a második testet, és így nagyobb erő nyomja a testeket egymáshoz, mint széttolja őket. A koncepciót az alábbi rajz szemlélteti.

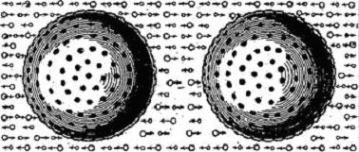
40-2 ábra A Fatio-féle tológravitációs elmélet illusztrációja. (Le Sage rajza)

Ahogy az éterelmélet a Michelson-Morley korában, Fatio elmélete is szenvedett a testek viselkedésének kinetikai értelmezései miatt. Lord Kelvin és mások rámutattak, hogy a testek és a csillagászati testek pusztán kinetikus kölcsönhatása hőt termel. 55,56,57,58

Egészen Planckig és Casimirig nem voltunk tisztában vele, hogy mik is azok a testecskék. A testecskék a vákuum-ingadozások és dipólusok. A Casimir-erőhöz hasonlóan a vákuum-ingadozások sem okozzák a testek felmelegedését.

Mivel a gravitáció, ahogy ismertük, valójában egy kétkomponensű erő, a Fatio-Casimir modell a nagyenergiájú gravitációs részre vonatkozik. A vákuum-ingadozások közötti Van der Waals erők olyan nyomást hoznak létre, amely minden testet megnyom. Az árnyékoló hatás miatt két egymástól távolodó test közötti nyomás csökken az őket összenyomó nyomáshoz képest. A nettó hatás az, hogy a testek egymáshoz tolódnak. A mechanikai erő magyarázza a sötét erőt, ahogy azt korábban a 24. fejezetben leírtuk.

Azt is fontos megjegyezni, hogy Fatio elmélete valódi kvantumgravitációs elmélet, mivel teljes mértékben kvantumelektrodinamikai elveken alapul. Ezenkívül egyesíti a gravitációs erőt az elektromágneses és mechanikai erőkkel. A Casimir-erő létezése azt sugallja, hogy a Fatio-Casimir-erőnek léteznie kell; ez nem is vita tárgya.

Ahelyett, hogy megpróbálnák kitalálni, hogyan gyorsulnak fel a testek a gravitáció hatására, a mainstream fizikusok úgy tettek, mintha elméleteik megmagyaráznák a gyorsulást, azonban ez hazugság.

Van még egy utolsó kérdés, ami eddig megakadályozta a Fatio-Casimir tológravitációs elmélet elfogadását, és így jön létre az 1/r 2 változó van der Waals erő? Ez a következő hazugság témája.

54 N Fatio de Dullier, „De le Cause de la Pesanteur” (kb. 1690), szerkesztett változat, kiadó: K. Bopp, Drei Untersuchungen zur Geschichte der Mathematik, Walter de Gruyter & Co. 1929. 19-26.

55 W. Thomson, (Lord Kelvin), "On the ultramundane corpuscles of Le Sage", Phil. Mag. 45: 321–332, 1873.

56 J. C. Maxwell, "Atom", egyikben sem, Encyclopedia Britannica, 3 (9. kiadás), 38–47. (1875).

87 H. Poincaré, "Theory of Lesage", A tudomány alapjai (Science and Method, 1908), New York: Science Press, 517–522. o., 1913.

58 R.P. Feynman, The Character of Physical Law, The 1964 Messenger Lectures, 37-39., 1967.

41. hazugság: A Van der Waals erők nem magyarázzák meg a gravitációt

A fizika legnagyobb hazugságai közül a 41. van der Waals erők nem magyarázzák a gravitációt. Amint azt korábban tárgyaltuk, a van der Waals-erők a dipólusok közötti kölcsönhatások következményei. Ebben az esetben a dipólusok vákuum-ingadozások. A nehézséget az jelenti, hogy az elektromos töltésdipólusok közötti van der Waals-erők hatótávolsága rövid.

Ezeknek a rövid hatótávolságú van der Waals-erőknek nincs mérhető hatása a csillagok közötti távolságra, mivel sokkal gyorsabban csökkennek, mint 1/r2. A gravitáció magyarázatához ezen erők némelyikének inverz négyzettörvényben kell következnie.

A Van der Waals-erők azonban az egyetlen ismert erőtípus a vákuum-dipólusok között, amelyek a gravitációhoz szükséges lökést képesek létrehozni. Következésképpen a tudósok megpróbálták levezetni a van der Waals-erőt, amely az inverz négyzettörvényt követi. 59 A mai napig ezek a próbálkozások nem jártak sikerrel. 60 Következésképpen a gravitációs hatás Fatio-Casimir elmélete nem kapott széles körű elfogadottságot.

A probléma része a fizikusok általános meggyőződése, hogy erők mágikus cselekvés révén hatnak távolról, és a mágikus sugárcsomagok vagy bármi hasonlók azok, amelyek meghajtást hoznak létre. Ha megpróbáljuk megérteni, hogy a vákuum hogyan befolyásolja a tárgyakat, például a mágneseket, fel kell ismernünk, hogy valamiféle kiterjesztett Casimir-erő valóban létezik.

Vákuum-ingadozási nyomás nehezedik minden testre, és ez a nyomóerő felelős minden mozgásért az elektromágneses, mechanikai és gravitációs erők miatt. Ezen erők mindegyike a távolság függvényében változik a fordított négyzettörvény szerint. Ez azt jelenti, hogy minden térben léteznie kell egy alapvető van der Waals nyomásnak, amely összhangban van a fordított négyzettörvénnyel.

Következésképpen nem foglalkozunk azzal a kérdéssel, hogy van-e 1/r2 változó van der Waals nyomás a térben. Az alapvető erőkre vonatkozó fordított négyzettörvény fizikai bizonyítéka azt mutatja, hogy létezik 1/r2 változó nyomású erő. Ennek tárgyi bizonyítéka megkérdőjelezhetetlen, mivel nincs más magyarázatunk a mozgásra, amely összhangban állna a vákuumdipólusok létezésével.

Tehát csak arról a kérdés van szó, hogyan származtatjuk ezt matematikailag. Az erő levezetésének korábbi kudarcai egyszerűen azt mondják nekünk, hogy még nem fedeztük fel az erő helyes fizikai magyarázatát az elektromágneses van der Waals erőelmélet keretein belül.

Ennek a nehézségnek az az oka, hogy a fizikusok általában nem vették észre, hogy a mechanikai erők térerőként viselkednek, és ezért léteznie kell egy második dipólusnak, egy mechanikus dipólusnak. Ennek a dipólusnak különböznie kell a pozitív és negatív elektromos dipólustól. A mechanikus tárgyaknak, például a forgólapoknak nincs elektromos töltése, és nem hoznak létre elektromágneses teret.

Amint azt más fejezetekben említettük, a legvalószínűbb mechanikai dipólus Dirac pozitív és negatív „energia” dipólusa, az anyag és az antianyag. Az 1/r2 változó van der Waals nyomáserő levezetése egyszerű, ha felismerjük, hogy két különböző típusú dipólus létezik, és mindegyik részecskének kétféle töltése van. Még az sem számít, ha a mechanikai dipólust másnak tekintjük, mint az anyagot és az antianyagot; valamilyen típusú mechanikus dipólus megléte elegendő a probléma megoldásához.

Ennek egyszerű az oka, ugyanis kétféle dipólus létezik, két különböző töltéspolaritás-kombinációval. Az egyik dipólus egyik végén pozitív elektromos és negatív mechanikai (anyag), a másik végén negatív elektromos és pozitív mechanikai (antianyag) töltéssel rendelkezik. Ennek a dipólusnak olyan töltései vannak, mint egy elektron-pozitron párnak.

Létezik egy második típusú dipólus is, amelynek egyik végén pozitív elektromos és mechanikai (anyag), a másik végén negatív elektromos és mechanikai (antianyag) töltés található. Ennek a dipólusnak olyan töltései vannak, mint egy proton-antiproton párnak.

41-1. ábra Két dipólus, egy elektronszerű és egy protonszerű, mindegyik szomszédos elektromos dipólusai kioltóak és anyag-dipólusaik taszítóak.

Ennek az a jelentősége, hogy ez a két különböző dipólus-típus mindig taszítja egymást, bármilyen irányultságú is legyen. Ne feledje, hogy az elektronok taszítják a protonokat, amikor közel kerülnek. Ha úgy sorakoznak fel, hogy pozitív és negatív elektromos töltéseik a közelben vannak, akkor mechanikai töltésük taszító igazodásban van (anyag az anyaghoz vagy antianyag az antianyaghoz). Ezt a 41-1. ábra szemlélteti. Ha viszont mechanikai töltéseik a közeli ellentétekhez igazodnak (az anyag az antianyaghoz), akkor elektromos töltéseik taszítják (pozitív a pozitív és negatív a negatív felé).

Ha valaki elutasítja azt az elképzelést, hogy a mechanikai erők egy térerő, akkor az elektronok, a protonok, valamint a protonok és elektronok közötti kis hatótávolságú taszító erők elegendőek az 1/r2 változó van der Waals nyomáserő létrehozásához, amikor elektrosztatikus taszítással kombinálják. Még ha ezeket az erőket a Pauli-féle kizárási elvnek akarjuk is tulajdonítani, ezeknek az anyagrészecskék közötti taszítóerőknek a bizonyított létezése elegendő az 1/r2 változó van der Waals nyomáserő magyarázatához.

Ez a helyzet egy teljesen új típusú van der Waals erőhöz vezet, egy olyan erőhöz, ahol állandó taszítás van a dipólusok között, függetlenül attól, hogy milyen irányban vannak. Ez az új van der Waals erő a forrása a gravitációért felelős 1/r2 változó nyomású erőnek, valamint az elektromágneses és mechanikai erők fordított négyzetes törvényének.

Az az elképzelés, hogy a van der Waals-erők nem magyarázzák a gravitációt, hazugság. Az elektromágneses erő a fordított négyzettörvényt követi, és az elektromágneses mozgást a kiterjesztett Casimir-erőnek kell okoznia. Ez azt jelzi, hogy a vákuumból származó 1/r2 változó van der Waals nyomásnak kell lennie. Ez a van der Waals-erő az anyagrészecskék közötti, valamint az antianyag-részecskék közötti taszító erőknek köszönhető.

59 H.E. Puthoff, „Gravitation as a Zero-Point-Fluctuation Force”, Phys Rev A 39:2333, 1989.

60 S. Carlip, Phys. Rev., 47: 3452, 1993.

42. hazugság: Az általános relativitáselmélet figyelmen kívül hagyhatja a nullapont energiát

A fizikában a 42. legnagyobb hazugság az, hogy az általános relativitáselmélet figyelmen kívül hagyhatja a nullapont energiáját. Ezt a hazugságot a legnagyobb vákuum-ingadozás-tagadónk, Albert Einstein lába elé rakhatjuk. Ő és mások, akik kidolgozták az általános relativitáselméletet, egyszerűen figyelmen kívül hagyták a nullapont energiáját, jól tudva, hogy ha nullapont energiát kellene hozzáadniuk az elmélethez, az nem fog működni.

Az éter tömegenergiája körülbelül 1095 gramm/köbcentiméternek felel meg, feltételezve, hogy a Planck-hossznál határértéket vesznek fel. Egy köbcentiméter vákuum több energiát tartalmaz, mint a teljes látható univerzum. Az általános relativitáselmélet modelljében minden energia felelős a gravitációs erőért. Tehát, ha a vákuumenergiát beleszámítanák az általános relativitáselmélet számításába, az univerzumban lévő összes anyag a gravitáció hatására a lehető legnagyobb sűrűségű anyagformába tömörülne, egy nagy fekete lyukba. Ennek tudatában a mainstream fizikusok, akik az általános relativitáselméletet részesítik előnyben, amit nagyra éltékelnek, továbbra is figyelmen kívül hagyják a vákuumenergiát, és állandósítják a hazugságot.

Vegye figyelembe, hogy a fekete lyuk-elmélet szerint egy köbcentiméter vákuum 1068 méter átmérőjű fekete lyukat hozna létre, amely körülbelül 1042-szer nagyobb, mint a látható univerzum. Tehát nyilvánvalóan a vákuumenergiának nincs gravitációs hatása a fényre vagy az anyagra.

A fizikusok hazugsága tovább súlyosbodik, ha figyelembe vesszük, hogy – ahogy Dirac először javasolta – a tömeg a vákuumenergia elmozdulásának köszönhető, így a tömegenergia egyenlő az eltolt vákuumenergiával. Ez azt jelenti, hogy a térben lévő teljes energia mindig egyenlő az üres tér kezdeti vákuumenergiájával. Következésképpen az univerzumban nincs energiagradiens. Az az elképzelés, hogy a gravitációt a térbeli teljes energiagradienshez viszonyítjuk, ostobaság.

Amint az utolsó hazugságban tárgyaltuk, a gravitációval kapcsolatos vákuumenergia-probléma könnyen megkerülhető. A vákuum ingadozása minden irányban egyenletes nyomást fejt ki, így az egyébként üres térben lévő testet minden oldalról egyformán nyomják. A test sem melegszik fel, amint azt a Casimir-erő bizonyítja. A Fatio árnyékoló hatása miatti nyomáskülönbségek gravitációs gyorsulást okoznak.

Az alap vákuumnyomás pozitív és egyenletes minden irányból. Más szóval, az éter anélkül gravitál, hogy érzékelhető gravitációs erőt hozna létre, mivel minden oldalról egyformán nyomódik. Csak nyomáskülönbség esetén észleljük.

Hazugság, hogy az általános relativitáselmélet figyelmen kívül hagyhatja a nullapont energiáját. A vákuum-ingadozások és az éter valóságosak, és ezeket minden gravitációs elméletben figyelembe kell venni.

43. hazugság: Görbült tér

A fizikában a 43. legnagyobb hazugság a görbült tér. Mint a fizika sok más nagy hazugsága, ez is az éter elutasításának eredménye. Ha figyelembe vesszük a nullapont energiáját, könnyen felismerhetjük, hogy nincs elég tömegenergia vagy más energiaforma a vákuum elmozdításához vagy más módon görbítéséhez. Túl sok a vákuumenergia ahhoz, hogy a tömegenergiának bármiféle hatása legyen. Ez a hazugság annak is az eredménye, hogy a fizikusok nem vették észre, hogy sokkal egyszerűbb magyarázata van a mechanikai erőjelenségeknek, amelyeket megpróbáltak megmagyarázni, mint például a Merkúr perihéliumának precessziója.

A vákuum tömeg-energia-egyenértéke ~1095 gramm/köbcentiméter, feltételezve, hogy a Planck-hossznál egy korlát-érték van. A vákuumenergia több mint 1094-szerese a Földön jellemző, nem vákuum energiájának. A látható világegyetem teljes tömegét 1056 grammra becsülték. 61 Tehát hogyan módosíthatja egy ilyen kis mennyiségű tömegenergia a vákuum geometriáját és a hozzá kapcsolódó nagy energiát? Ez nem lehetséges. A tömeg az összes többi nem-vákuum energiával együtt egyszerűen nem módosíthatja a vákuumot semmilyen módon, csak egy nagyon kis mennyiségű vákuumenergia kiszorítására.

Ezt a hazugságot tovább súlyosbítja, ha figyelembe vesszük, hogy a stabil részecskék, az elektron, a proton és a neutron tömegenergiája megegyezik az általuk kiszorított vákuumenergiával. Ebből arra következtethetünk, hogy a térben a teljes energia állandó. A térhez nincs energiagradiens, így a térgörbület gondolata teljes nonszensz.

Történelmi szempontból a görbült tér modelljét azért fejlesztették ki, mert a fizikusok nem ismerték fel, hogy a mozgó anyag ugyanolyan típusú erőket hoz létre, mint a mozgó elektromos töltések (lásd a 24. hazugságot). A forgó testek, például a bugócsigák és a giroszkópok vákuum-ingadozási dipólusok forgó mezőit állítják elő, amelyek lehetővé teszik, hogy a forgó testek a vákuumnak ütközzenek. Hasonlóképpen, minden test és részecske a vákuumot tolja.

A mechanikai erő sokkal szélesebb skálán jelenik meg, mint az csak egyszerű forgó csúcsoknál tapasztalható. Az anyagtestek közötti lineáris mechanikai erő hatására az anyagtestek felgyorsulnak egymástól. A Nap forgása a bolygók elliptikus pályáinak precesszióját okozza. A forgó galaxisok csillagaira ható mechanikus Lorentz-erők hatására a csillagok spirálokká alakulnak. Még a csillagokban és bolygókon belül is a forgás ellentétes forgást okoz, ami dinamóhatásokhoz vezet. Összességében a mechanikai térerő megmagyarázza mindazokat a jelenségeket, amelyeket népszerűen a görbült térmodellnek tulajdonítanak.

Az ívelt térmodell komoly nehézségekbe ütközik, ha kettőnél több objektumot veszünk figyelembe, amelyek nagyon eltérő pályán vannak. Például a Földnek közel kör alakú pályája van, de a Föld közelében elhaladó üstökös nagy ellipszis alakú pályát követ, amely közel merőleges a Föld pályájára. Hogyan lehet a teret egyszerre két merőleges irányba görbíteni? Semmi értelme.

Ha figyelembe vesszük, hogy több millió foton keresztezi a tér egyetlen pontját különböző irányokból, akkor ennek még kevésbé van értelme. Nincs értelme ívelt térmodellt elfogadni, ha egy geometriailag sík térmodell működik, és működik, ha van éter. Miért vágynak a fizikusok egy ilyen bonyolult és szükségtelen modellre? Valószínűleg azért teszik ezt, mert a sci-fin szórakoztatóbb és érdekesebb gondolkodni, mint a valódi tudományon. Viszont bármely igazi tudós a sík tér geometriáját részesíti előnyben az ívelt tér geometriájával szemben, és megfelelő síktér-elméleteket keres. Ja, és nem mellesleg a CMB egységessége bizonyítja, hogy az éter-nyugalmi állapot geometriailag sík.

A görbült tér egyértelműen a fizika egyik legnagyobb hazugsága. Óriási, szükségtelen visszalépése volt ez a fizikusoknak, hogy a világegyetem működését megértsék.

61 P. Davies, The Goldilocks Enigma, First Mariner Books, p. 43, 2006

44. hazugság: Általános relativitáselmélet

A fizika legnagyobb hazugságai közül a 44. az általános relativitáselmélet. Az utolsó néhány hazugság után nyilvánvalóan jön ez a hazugság. Mint a fizika sok más nagy hazugsága, ez is nagyrészt a vákuumenergia tagadásának köszönhető. Ha ugyanis a vákuumenergiát vesszük figyelembe, az általános relativitáselmélet kudarcot vall.

A fizikusok korábban azt sem ismerték fel, hogy még a legegyszerűbb mechanikai erőkölcsönhatások is, mint például a tehetetlenség és a gravitáció, melyek a forgó giroszkópokkal ellentétes erőt fejtenek ki, megkövetelik, hogy legyen egy alapvető mechanikai erő, amely magában foglalja a vákuum-ingadozások mezőit is. Íme egy rövid lista az általános relativitáselmélet modelljének néhány legjelentősebb hibájáról.

A. Ez összeegyeztethetetlen az éter ismert létezésével, mivel az éter-nyugalmi állapot a vákuum-ingadozásokból származó fizikai és időbeli méretei egységesek, és geometriailag sík.

B. Nem magyarázza meg, hogy a tömegenergiáról és más, nem-vákuumenergiáról szóló információk hogyan jutnak el azonnal az univerzumba.

C. Nem magyarázza meg, hogyan gyorsulnak fel a testek.

D. Túl kevés anyag van az univerzumban ahhoz, hogy az általános relativitáselmélet modellje érvényes legyen, ez az úgynevezett hiányzó anyag vagy sötét anyag problémája.

E. Nem magyarázza meg fizikailag, hogyan görbül a tér.

F. Nem magyarázza meg, hogy a tér különbözőképpen görbül ugyanabban a pontban és időben különböző sebességgel és/vagy irányban mozgó testek vagy fotonok számára.

G. Ha a nullponti energiát is beleszámítanák, az általános relativitáselmélet modelljének együtthatóinak megváltoztatása nélkül, az univerzum a lehető legkisebb térfogatra omlana össze.

H. Ha az általános relativitáselmélet modelljébe a nullpont energiáját is beszámítanák, és az együtthatókat állandó vákuumenergiát feltételezve módosítanák, a gravitációs hatások elhanyagolhatóak lennének, mivel a nem-vákuum energia az összenergia elenyésző százalékát teszi ki.

I. A tér összenergiája állandó, miután felismertük, hogy a tömeg és az egyéb energiaformák egyenlők az általuk kizárt vákuumenergiával, így a teljes energiasűrűségben nincs változás, és nincs alapja annak, hogy a gravitáció a lokális energiasűrűség változásának tudható be.

J. Ha a nullponti energiát beleszámítjuk, nincs elegendő tömegenergia a tér görbítéséhez.

K. Egy alapvető mechanikai erő könnyebben megmagyarázza az általános relativitáselmélet úgynevezett bizonyítékait, és még több kapcsolódó jelenséget, amelyet az általános relativitáselmélet nem magyaráz meg.

L. Ha van választási lehetőség, a sík térmodell előnyösebb, mint a görbült térmodell.

M. A CMB egységessége tudományos bizonyítéka annak, hogy az éter-nyugalmi keret geometriailag sík.

N. A sötét erőt, a nagyenergiájú gravitációs erőt és a mechanikai erőt nem lehet egyetlen görbült térmodellben összevonni.

O. A nagyenergiájú gravitációt legjobban a Fatio-Casimir erő magyarázza, amelynek amúgy is léteznie kell.

P. Lehetetlen, hogy mind a Fatio-Casimir erő, mind az általános relativitáselmélet egyszerre létezzen.

Az általános relativitáselméletnek természetesen számos egyéb megvalósítási szintű problémája is van, de ezek az alapvető hibák azt mutatják, hogy az általános relativitáselmélet soha nem volt érvényes, és nem is kellett volna figyelembe venni.

45. hazugság: Gravitációs idődilatáció

A fizikában a 45. legnagyobb hazugság a gravitációs idődilatáció. Íme egy olyan koncepció, amelyet a fizikusok több szinten elrontanak a számos tévhit és hazugság miatt. Azt tudjuk, hogy az órák lassabban járnak az anyagtestek, különösen a Föld közelében, ahogy ezt kísérletileg is bebizonyították. A legtöbb bizonyíték a pályán lévő órák órajeleiből származik, különösen a globális helymeghatározó rendszerben használtakból. A GPS-órák gyorsabban futnak a Földhöz viszonyított helyzetük miatt, és valamivel lassabban a sebességük miatt, azzal a nettó különbséggel, hogy gyorsabban futnak, mint a földi órák, miközben még a Föld felszínén vannak.

Szóval most valószínűleg néhányan azon gondolkodnak, hogy ez hogyan lehet hazugság, ha bebizonyosodott? A hazugság azért van, mert a mainstream fizikusok valójában nem azonosították az óra lassításáért felelős fizikai mechanizmust. Az az elképzelés, hogy az óra lassulása összefügg a gravitációval és a tér valamiféle kitágításával, csupán rossz feltételezések, amelyek együtt hazugságot alkotnak.

Ahogy korábban említettük, a gravitáció két vagy három erő összege, tehát a gravitáció miatti óralassulásnak minden erőtől függetlenül kell bekövetkeznie. Ehhez általánosabb modellre van szükség, mint egyszerűen azt mondani, hogy a gravitáció felelős az óra lassításáért.

Ugyancsak a 16. hazugságban említettük, hogy a tér idődilatációja hazugság a speciális relativitáselméletben. A tér időbeli dilatációja szintén hazugság az általános relativitáselmélet vagy bármely más gravitációs modellben. A 16. hazugságot cáfoló érvek miatt az sem lehetséges, hogy két ellentétes, de megközelítőleg egyenlő erő által téridő-tágulás történjen.

Hasznos megérteni az ekvivalencia elvét. Általában ez az a kijelentés, hogy a gravitációs és a tehetetlenségi tömeg, vagy a gravitációs és a tehetetlenségi gyorsulás nem különböztethető meg. Az Einstein által használt egyenértékűségi elv legegyszerűbb példája a lift. Amikor egy lift felfelé vagy lefelé gyorsul, a versenyzők nehezebbnek vagy könnyebbnek érzik magukat. Ezek a hatások megkülönböztethetetlenek egy magasabb vagy alacsonyabb felszíni gravitációjú bolygón való erőhatásoktól.

Az ekvivalencia-elv azt mondja nekünk, hogy az óra lassulását nem csak a gravitáció okozza, mivel bármi okozhatja, ami gyorsulást okoz, vagy akárcsak a tehetetlenséget. Általában az ekvivalencia elvét közvetlenül a potenciális energiához kell kötni. Vagy az ekvivalenciaelv még tágabb értelmezésében az órajelek nem közvetlenül a tehetetlenséghez, a gyorsuláshoz vagy a potenciális energiához kapcsolódnak, hanem a nullponti mező valamely más tulajdonságához. A legalapvetőbb formájában azt mondja nekünk, hogy a mechanikai erők és a gravitációs erők ugyanúgy befolyásolják az órajelet.

Ahhoz, hogy ténylegesen megfejtsük az órajelek változásával kapcsolatos rejtvényt, tudnunk kell, hogy milyen fizikai dolog szabályozza az egyetemes órajelet, és mi lassítja azt az anyagtestek közelében. Először is, a szabványos órák az éter nyugalmi keret vákuum-ingadozásai. Az univerzális órajel, amely a lehető leggyorsabb órajel (nem Casimir-üregben 62 ), akkor érhető el, ha egy óra nyugalomban van az éter nyugalmi keretéhez képest, feltéve, hogy nincs anyag a közelben. Az órajelet ugyanazzal a mechanizmussal kell szabályozni, amely a vákuum ingadozását szabályozza.

A relativitáselméletből kiindulva, amint azt a 16. hazugság tárgyalja, az órajelek lelassulnak, ha az órák ehhez az univerzális nyugalmi kerethez képest sebességgel mozognak. Ez azt mutatja, hogy az órajel-változásnak a vákuum-ingadozásokkal való kölcsönhatások miatt kell lennie, vagy hogy megfordítsuk, a vákuum-ingadozások szabályozzák az órajeleket.

Itt meg kell jegyeznünk, hogy a vákuumfluktuáció a fénysebességhez tartozó maximális hullámhosszal (távolsággal) és frekvenciával (idővel) forog, c = λν . A fénysebesség a mozgó nyugalmi keretekben és az anyagtestek közelében is ugyanolyan mértékben lassul, mint a lassuló órajel.

A vákuum-ingadozások forgása lelassul a vákuum van der Waals nyomatékának a környező vákuum-ingadozási mező által kiváltott növekedése miatt. A van der Waals nyomaték nagyobb, ha mozgó nyugalmi keretben mérjük, és nagyobb egy anyagtest közelében is. Amikor a van der Waals nyomaték növekszik, az órák lelassulnak.

A gravitációs idődilatáció tehát hazugság. Az óra lassulása nem közvetlenül a gravitációnak köszönhető, és a tér nem tágul.

62 A Casimir-üreg belsejében bizonyos vákuum-fluktuációs hullámhosszak ki vannak zárva. A hullámhosszak kizárása a vákuum van der Waals nyomatékának csökkenéséhez vezet. Klaus Scharnhorst feltételezte, hogy a Casimir-üregben nagyobb a fénysebesség. 63,64 Ha ez igaz, akkor az is, hogy a Casimir-üregben gyorsabbak az órajelek. A fénysebesség és az órajel változása arányos.

63 G. Barton, K. Scharnhorst (1993). "QED párhuzamos tükrök között: c-nél gyorsabb vagy a vákuum által felerősített fényjelek". Fizikai folyóirat A. 26 (8): 2037.

64 K. Scharnhorst, "A fény sebessége módosított QED vákuumban". Annalen der Physik. 7 (7–8): 700–709, 1998. arXiv:hep-th/9810221.

46. hazugság: A gravitációs időtágulás az általános relativitáselmélet bizonyítéka

A fizika legnagyobb hazugságai közül a 46. a gravitációs idődilatáció az általános relativitáselmélet bizonyítéka. Természetesen, ha az általános relativitáselmélet hazugság, ennek az állításnak is hamisnak kell lennie. Ezt az állítást azonban újra és újra megismétlik az általános relativitáselmélet modelljének hívei, így megérdemli, hogy helyet kapjon a fizika ostobaságok top 100-ában.

A fizikusok egyszer sem mondják el nekünk, hogyan változnak a fizikai órajelek az általános relativitáselmélet modellje miatt. Legjobb esetben azt a homályos érvet kapjuk, hogy az óra lassul, ha felgyorsítják, anélkül, hogy megmondanánk, hogy a gyorsítás hogyan lassítja az órát. Vagy ami még rosszabb, azt mondják, hogy a térnek megvan a maga órája, amely a gravitáció, a tér mitikus időtágulása miatt valahogy lelassul. Az egyetlen fontos információ, amit ebből kaptunk, az az, hogy a mechanikai és a gravitációs erők ugyanúgy változtatják az órajelet.

Az az állítás, hogy a gravitációs idődilatáció az általános relativitáselmélet bizonyítéka, hazugság. A 45-ös hazugság alapján könnyen belátható, hogy az órajelnek semmi köze a gravitációhoz, legalábbis nem közvetlenül, és nincs tágulás. Az órajel-sebességek a vákuum-ingadozások forgási sebességéhez kapcsolódnak helyi körülmények között, tekintettel az anyagnak az éter nyugalmi keretéhez viszonyított közelségére és sebességére.

47. hazugság: Az ekvivalencia elv bizonyítja az általános relativitáselméletet

A fizikában a 47. legnagyobb hazugság az ekvivalencia-elv, amely az általános relativitáselméletet bizonyítaná. E fejezet megírásnak a napján nyílt meg az elavult fizika bástyájának, a Wikipédiának az ekvivalenciaelv oldala:

Az általános relativitáselmélet fizikájában az ekvivalenciaelv a gravitációs és a tehetetlenségi tömeg ekvivalenciájával foglalkozó számos rokon fogalom bármelyikére vonatkozik.(…)Einstein azt javasolta, hogy emeljék az általános elv státuszává, amit ő „az egyenértékűség elvének” nevezett, amikor a relativitáselméletét megalkotta…

Itt van tehát egy eset, amikor Einsteinnek igaza volt. Az ekvivalencia elve általános elv. Az ekvivalencia elve igaz, még akkor is, ha az általános relativitáselmélet hazugság.

Az ekvivalencia-elv álarcában a tehetetlenségi tömeget inkább ál-, semmint valódi erőnek tekintik, és ezt az ál-erőt egy valós erővel, a gravitációval egyenértékűnek mondják. A nyilvánvaló hiba itt az, hogy mindketten valódi erők. A tehetetlenségi erő valódi mechanikai erő, és nem pszeudo-erő.

Az ekvivalencia elve leegyszerűsíthető, ha csak azt mondjuk, hogy az erő az erő. Az ekvivalenciaelv valójában nem biztosít mechanizmust az anyagtestek vagy fotonok közötti gravitációs kölcsönhatásokhoz, így valójában nem oldja meg a kapcsolódó fizikai problémákat. Ez egy másik szabály, amely figyelmen kívül hagyja a mögöttes fizikai mechanizmust, a tényleges fizikát. Ez azonban jobb módot ad bizonyos problémákra, ha megfordítjuk a szemléletet.

Ahelyett, hogy azt mondanánk, hogy a tehetetlenség egyenértékű a gravitációval, azt kellene mondanunk, hogy a gravitáció egyenlő a tehetetlenséggel. A gravitációs erő megegyezik az éter által a testre kifejtett kombinált elektromechanikus erőkkel. Vagy még általánosabban, a gravitáció nem is erő, mivel az elektromágneses és mechanikai erők az alapvetőek.

Az az állítás, hogy az ekvivalenciaelv bizonyítja a relativitáselméletet, hazugság. Einstein az ekvivalencia-elv értelmezését használta fel általános relativitáselméletének alátámasztására, míg az ekvivalenciaelv valójában egy különálló magasabb szintű elv. Az erő az erő.

48. hazugság: Sötét anyag

Az a tény, hogy a galaxisok és galaxishalmazok dinamikája nem egyezik a standard gravitációs elmélettel a megfigyelt vagy világító anyaggal, elvileg kétféleképpen magyarázható: rossz gravitációs elméletet használunk, vagy nem látjuk az összes anyagot. Ez utóbbi az elterjedtebb nézet. Arról azonban nincs egyértelmű konszenzus, hogy mi lehet a sötét anyag. 65

Paul S. Wesson

A fizika legnagyobb hazugságai közül a 48. a sötét anyag. Úgy gondolják, hogy a sötét anyag az univerzumban más anyag, mint a protonokból, neutronokból és elektronokból álló normál anyag. A fizikusok azért hisznek a sötét anyagban, mert a népszerű gravitációs modellek helyes működéséhez szükséges anyag 70-90%-a hiányzik. Ezt az anyaghiányt spirálgalaxisokban és galaktikus halmazokban fedezték fel, ahol a csillagok, illetve a galaxisok sebessége túl nagy volt ahhoz, hogy a gravitáció önmagában összetartsa őket, tekintettel a jelenlévő tömeg nagyságára. Ezért ezt nevezik hiányzó tömegnek, hiányzó sötét anyagnak vagy csak sötét anyag problémának, és gyakran a fizika tíz megoldatlan problémája közé sorolják.

A fizikusok még mindig azt akarják hinni, hogy a gravitációs modellek helyesek, még akkor is, ha 90%-ban tévesnek tűnnek. Ez olyan, mintha ha egy vizsgán csak a kérdések 10%-ára válaszolna, mégis 100%-osan ismernék el a teljesítményét. Ez a hozzáállás mindenki számára megdöbbentő, akinek van józan esze. Egy dolog ragaszkodni egy olyan elmélethez, amely fokozatos fejlesztést igényel, és egy másik dolog támogatni egy olyan elméletet, amely szinte teljesen hibás.

A helyes következtetésnek mindvégig az kellett volna lennie, hogy a fizikusok rossz gravitációs elméletet alkalmaznak, vagy további, jelenleg nem ismert erők működnek. Ennek még világosabbnak kell lennie most, hogy tudjuk, hogy a népszerű gravitációs elméletek valójában két vagy három erő kombinációját próbálják modellezni.

A spirális galaxisok kialakulásának megértésével kapcsolatos probléma könnyen megoldható, ha figyelembe vesszük a mechanikai erőt. A csillagok tangenciális sebessége egy forgó galaxisban egy mechanikus Lorentz-erőhöz vezet, amely a gyorsan mozgó csillagokat a galaxis közepe felé löki. E Lorentz-erő nélkül a spirálgalaxis legkülső csillagai az intergalaktikus térbe repülnének. Ez az erő megoldja a galaktikus klaszter sebességi problémáját is.

Az alapvető elektromágneses erőknél ismert, hogy két párhuzamos, azonos irányú áramot vivő vezeték vonzza egymást. Ugyanez igaz két párhuzamos úton lévő csillagra is. Így alkotnak sávokat a csillagok a forgó galaxisokban. A mechanikai erő nélkül galaktikus spirálok nem léteznének. Soha nem volt probléma a sötét anyaggal; mindig is hiányzó erő volt a probléma.

Így a sötét anyag elképzelése hazugság. A jelenlegi ismert gravitációs modellek vagy hiányosak, vagy teljesen hibásak.

65 P. Wesson, Fundamental Unsolved Problems in physics and Astrophysics, előkészítve a California Institute for Physics and Astrophysics számára,  http://www.calphysics.org/problems.pdf

49. hazugság: Gravitonok

A fizika legnagyobb hazugságai közül a 49. a graviton. Mint korábban említettük, a gravitonok hipotetikus elemi részecskék, amelyekről azt mondják, hogy a gravitáció mérőbozonjai. Más szavakkal, ez egy intelligens részecske, amelynek feladata a gravitációról szóló információk átvitele részecskéről részecskére és testről testre. Amint azt a 18. hazugságban tárgyaltuk, minden mérőbozon-modell hazugság a fizikai valósággal kapcsolodó számos következetlensége miatt, ez a gravitonokra épp úgy vonatkozik.

A gravitonok egy módja annak, hogy a newtoni gravitációs elméletet az elektromágneses elmélethez hasonlóvá alakítsák. Az elektromágneses esetben a fotonokat tekintik a mérőbozonnak vagy erőhordozónak (7. hazugság). Annak érdekében, hogy a gravitációs elméletet jobban hasonlítson az elektromágneses elmélethez, a fizikusok feltalálták a graviton hipotézist. Vegyük észre, hogy Einstein általános relativitáselméleti modellje nem támaszkodik a gravitonra, mivel ezek szerint a térgörbék létrejötte valami titkos, pillanatnyi kézfogás lenne az univerzumban található összes anyaggal és energiával, ahelyett, hogy a testek egy erő hatására mozognának.

Annak ellenére, hogy a gravitonok soha nem jutottak túl a hipotetikus elméleti szakaszon, és sem közvetlenül, sem közvetve nem észlelték őket, még mindig szerepelnek az elemi részecskék szabványos modelltáblázataiban.

A gravitonok kitalálóinak sohasem kellett volna idáig eljutniuk. A valódi kvantumgravitációban, ahogy azt Fatio és Casimir leírta, a vákuum-ingadozások felelősek a vákuumnyomásért, amely a gravitációt okozza, és lökést ad a testeknek, hogy felgyorsítsák azokat. Fatio-Casimir kvantumgravitációja teljes mértékben összhangban van az elektromechanikus erőelmélettel, és annak része. Nincs szükség gravitonokra. Graviton egy hazugság. Gravitonok nem léteznek, és soha nem lett volna szabad egyetlen elmélet részévé sem tenni.

50. hazugság: A gravitáció az energia minden formájának köszönhető

A fizikában a legnagyobb hazugságok 50. része az, hogy a gravitáció az energia minden formájának köszönhető. Az általános relativitáselmélet részeként Einstein azt feltételezte, hogy az energia minden formája gravitál vagy gravitációt okoz. Ez a rossz feltételezés részben felelős a modern éterelmélet lassú elfogadásáért. Amint arról korábban szó esett, ha a nullponti energia gravitál, az általános relativitáselmélet modellje szerint az univerzum egy fekete lyukba tömörülne.

Einstein tette ezt a feltételezést, mivel Poincaré, Pietro Olinto és később maga Einstein kimutatta, hogy az anyag és az energia egyenértékűek az E = mc2 képlettel, vagy ahogy Poincaré közzétette, m = E/c2 . 66,67,68 Ennek ellenére mások is fontolgatták ezt az összefüggést Poincaré előtt.

Newton gravitációs elmélete szerint a gravitáció arányos a tömeggel. Tehát Poincaré megállapításának nyilvánvaló kiterjesztése az volt, hogy mivel az energia egyenlő a tömeggel, az energiának gravitációhoz is kell vezetnie.

Ez vezetett a kérdésekhez: a nullpont energia gravitál vagy nem? Ha gravitál, ahogy azt az általános relativitáselmélet modellje megköveteli, akkor érvényteleníti a modellt. Ha nem gravitál, az érvényteleníti Einstein feltevését! És ha az általános relativitáselmélettel összeegyeztethetetlen módon gravitál, érvényteleníti a modellt. Azaz nem számít, milyen variációban, de a nullpont energia nagy probléma az általános relativitáselmélet modelljében. Így Einstein és követői nagy éter-elutasítókká váltak, ha már korábban nem lettek azok.

A Fatio-Casimir effektus alapján a nullponti energia igenis gravitál. A testeket vonzó és taszító van der Waals erők révén gravitál. Ennek azért nincsenek katasztrofális következményei, mert a nyomás szinte tökéletesen egyenlő minden irányból. Ez a hatás nem omlik össze, és a részecskék nem esnek össze e nyomás alatt.

Csak kis nyomáskülönbségek vezetnek mozgáshoz, ami azt az erőt eredményezi, amelyet gravitációnak nevezünk. A gravitáció valójában nem egy különálló erő, hanem csak egy másik eredmény a vákuumenergia által keltett van der Waals-erők miatt, mely az elektromágneses és mechanikai erőelmélet része.

Az a feltételezés, hogy a gravitáció az energia minden formájának köszönhető, hazugság. Legalábbis hazugság az általános relativitáselmélet modelljében. Azt a kérdést, hogy mi okozza a gravitációt, a következő hazugság tárgyalja.

66 J.H. Poincaré, Arch. neerland. Sci., 2, 5,232, 1900, J.H. Poincaré, In Boscha, 1900:252.

67 O. De Pretto: "Ipotesi dell'etere nella vita dell'universo (Az éter hipotézise a világegyetem életében)." "Reale Istituto Veneto di Scienze, Lettere ed Arti" (The Royal Veneto Institute of Science, Letters and Arts) LXIII (II): 439–500. (elfogadva 1903. november 23-án és kinyomtatva 1904. február 27-én).

68 A. Einstein, „Zur Elektrodynamik bewegter Korper”, Annalen der Physik 17:891, 1905.

51. hazugság: A gravitáció a tömegnek köszönhető

A fizika legnagyobb hazugságai közül az 51. a gravitáció a tömegnek köszönhető. Megdöbbentő lehet, hogy bárki megkérdőjelezheti azt a Newton kora óta elfogadott elméletet, amely szerint a tömeg okozza a gravitációt, de a Fatio-Casimir effektus megléte újra megnyitja ezt a kérdést. Ha jobban belegondolunk, soha nem született sikeres válasz arra a kérdésre, hogy a tömeg pontosan hogyan okozza a gravitációt. Szóval, talán ez soha nem is a tömeg miatt volt.

Úgy tűnik, hogy a tömeg-gravitáció kapcsolat nagyon jól működik, de gyakran elfelejtjük, hogy a testek tömegei valamelyest körkörös levezetésből származnak. Meghatározzuk például a Jupiter tömegét úgy, hogy megmérjük a pályáját, és a Newton-egyenlet alapján kiszámítjuk a tömegét, majd azt mondjuk, hogy rendelkezik ezzel a tömeggel. A Jupiter tömegét független eszközökkel nem tudjuk mérni, mivel az űrben nincs olyan skála vagy mérleg, amelyet használhatnánk. Valóban fele akkora-e a Szaturnusz sűrűsége, mint a Jupiternek, vagy ez csak egy feltevés a gravitációs elméletből hiányzó további erő miatt. Jelenleg bízunk abban, hogy Newton képlete helyes, és haladunk tovább.

Soha nem gondoljuk, hogy mivel Newton és követői nem tudják, hogy a tömeg hogyan okozza a gravitációt, talán a Jupiter vagy a Szaturnusz tömege némileg különbözik, és a gravitáció tényleges oka valami más lehet. Ennek ellenére a newtoni modell olyan jól működik, legalábbis a Naprendszerben, hogy a tömegnek jó közelítésnek kell lennie ahhoz, hogy mi okozza a gravitációt.

Elgondolkodhatunk a gravitáció elfogadható fizikai magyarázatán, ha alaposabban megvizsgáljuk a Fatio-Casimir hatást. Fatio felismerte, hogy amikor egy testet mozgatnak, az erőt nem szabad tökéletesen átvinni a test másik oldalára, különben az árnyékhatás nem jön létre. Ez azt jelenti, hogy a vákuumenergia rányomja a részecskéket, de a részecskék nem egyformán nyomják az ellenkező oldalon lévő vákuumenergia-dipólusokat. Ez rugalmatlan válasz, mivel az energia egy része valahogy elvész. Ez az energiaveszteség vezet az árnyékoló hatáshoz, ami a gravitációhoz vezet.

Röviden szólva Fatio azt is felismerte, hogy a testeknek többnyire üres térnek kell lenniük, különben az általa javasolt erő túl erős lenne. Talán ő volt az első, aki felismerte ezt a tényt.

Ha ezt a részecske szemszögéből nézzük, akkor a vákuum-ingadozások van der Waals erői képesek rányomni a részecskét, de a részecske nem, vagy kevésbé képes visszanyomni. Ez a különbség okozza a gravitációt a részecskeszinten. Ez is elárul egy kicsit a részecskék szerkezetéről, de ez a nyúlnak egy nagyon mély ürege, amelybe ebben a könyvben nem fogunk belemenni.

Hogyan viszonyul ez a szerkezeti különbség a tömeghez? A válasz a mérettől függ. A kisebb vákuum-ingadozások energikusabbak, és amikor van der Waals erők nyomják a részecskéket, ez a lökés olyan vákuum-ingadozásokból származik, amelyek körülbelül akkora méretűek, mint az általuk rányomott részecskék.

A legnagyobb gravitációs erő ekkor a legkisebb részecskékre, a protonokra és a neutronokra hat. A nagyobb elektronokra gyakorolt nyomás sokkal kisebb, így az elektronok kisebb hatást fejtenek ki egy nagyjából azonos számú protonból és elektronból álló testben.

Ez a kapcsolat Dirac tömegenergiáról alkotott elképzelésén alapul, amit számításaim is megerősítenek; hogy a részecske tömege összefügg az átmérőjével és a részecske által kiszorított vákuum-ingadozási hullámhosszokkal. A tömeg gyakorlatilag egy másik méretmérő, ha a tartósan stabil részecskékről van szó.

És mi a helyzet a tömeg vagy energia más formáival? Minden azon múlik, hogy akadályozzák-e és hogyan a van der Waals-erők átadását. Ha egy vákuum-ingadozás egy mozgó test tehetetlenségi mezejének részeként forog, és így ténylegesen tehetetlenségi tömeg, akkor kevésbé valószínű, hogy reagál más dipólusokra a tipikus van der Waals-kölcsönhatásokban.

Végső soron a nullponttól eltérő energia és tömegenergia minden formája annak köszönhető, hogy a nullponti dipólusok részt vesznek bármely folyamatban, amely ezt az energiát termeli vagy tárolja. Amint a dipólusoknak más funkciójuk van, csökken a van der Waals erők átvitelének képessége.

Azt állítani, hogy a gravitáció a tömegnek köszönhető, hazugság. A gravitáció annak köszönhető, hogy a részecskék rugalmatlan válaszolnak a van der Waals erőkre a vákuum-ingadozások között, ami a Fatio-Casimir effektushoz vezet. Ezeknek az erőknek az erőssége a részecskemérethez kapcsolódik, amely azután a tömeghez van kötve. Más vákuum-ingadozások, amelyek olyan folyamatokhoz kötődnek, amelyek vákuum-ingadozási mező formájában energiát termelnek vagy tárolnak, szintén gátolják a van der Waals-erők átvitelét, ami gravitációs hatáshoz vezet.

Mindezek ellenére a tömeg valószínűleg továbbra is a gravitáció mérnöki célú közelítésének legegyszerűbb módja marad.

52. hazugság: A Pauli-féle kizárási elv

A fizikában az 52. legnagyobb hazugság a Pauli-féle kizárási elv. A Pauli-kizárási elv a kvantummechanikában az az elv, amely szerint két azonos fermion, ½ spinű önmagában teljes egész spinrészecske, például elektronok, nem foglalhatják el egyszerre ugyanazt a kvantumállapotot. Vegye figyelembe, hogy ez az elv nem vonatkozik a bozonokra, például a fotonokra. A hazugság ebben az esetben nem abból fakad, hogy két részecske nem ugyanazt az állapotot foglalja el, hanem az, hogy a fizikát nem a fizikai jelenségek magyarázata felől közelíti meg.

A baj a spinnel kezdődött, mivel a spin egy nem fizikai tulajdonság, és azt mondják, hogy ez a részecskék belső tulajdonsága. Soha nem létezett fizikai modell a pörgésre, és még a pörgés szó is helytelen gondolkodásmód lehet. Másrészt, amikor a fizikusok egyszer képesek lesznek fizikailag leírni a részecskéket, hogy akkor ez a spin miféle spin lesz majd, azt egyszerűen még nem tudjuk. A kizárási elv és a spin volt a kezdete annak, hogy a fizikusok önkényes, szabályalapú megközelítést alkalmaztak a részecskék tulajdonságaival kapcsolatban, ahelyett, hogy a tulajdonságokat fizikai jelenségekre alapozták volna. Más szóval, nem valós fizikát végeznek.

A héliummag körül keringő két elektronnak például két különböző spinállapota van, tehát eltérő kvantumállapotban vannak. Köztudott, hogy ezek az állapotok különböző átmeneti energiákhoz vezetnek, tehát valami fizikailag történik, csak fogalmunk sincs, hogy mi az. Aztán ezt a tanácstalan, szabályalapú megközelítést az energiaállapotok különbségének megértéséhez egy szélesebb spin-elméletté bővítik.

Vegye figyelembe, hogy az atomelméletben az első három kvantumszám a főkvantumszám, az azimutális vagy szögimpulzus-kvantumszám és a mágneses kvantumszám. Mindegyik fizikai tulajdonságon alapul. Az elvi kvantumszám a Bohr-modell perspektívájából egy elektron esetében az éppen elfoglalt héj, amely lényegében az atommagtól való távolsághoz kapcsolódik. Ezt a távolságot kvantáltnak mondják, mivel csak bizonyos távolságokat vagy energiaállapotokat lehet elfoglalni. A részecske szögimpulzusa és mágneses tere is ezeken a valós fizikai tulajdonságokon alapul. Az elektromos töltés a másik kvantumszám, amelyet általában belső tulajdonságként kezelnek, de valószínűleg fizikai tulajdonság, erről a következő fejezetben olvashat bővebben.

A spin-kvantumtulajdonság a Pauli-kizárási elvből következő első tévedés, de azóta ez az elv még sokszor megbukott. Minden alkalommal, amikor ez az elv csődött mond, egy új kvantumtulajdonságot találnak ki a hiba kijavítására, és ezeknek az új látszat-kvantumtulajdonságoknak nincs fizikai alapja. Ezeket a további kvantumszámokat ma már gyakrabban ízeknek nevezik.

Egyéb ízek közé tartozik a gyenge izospin, a leptonszám, a barionszám, a túltöltés, a furcsaság, a felsőség és a mélység. Aztán ezeket és más kitalált belső kvantumtulajdonságokat egyesítették, hogy egy numerológiai részecskeelmélet, a kvantumkromodinamika, más néven kvarkelmélet alapját képezzék. Sajnos ezeknek a tulajdonságoknak egyikére sincs fizikai magyarázat. A részecskefizikusok egyszerűen elfelejtik, hogy úgynevezett fizikai magyarázatokat kell készíteniük. Elfelejtik, hogy fizikusok.

A Pauli-féle kizárási elv a fizika egyik szabályalapú elve, amelynek nincs alapja a fizikai valóságban, és nem is igazán érdemes elvnek nevezni. A részecskék nem „ismerik” ezt a szabályt. Ez az elv egy példa arra, hogy milyen veszélyek fenyegetnek, ha önkényes szabályokat állítunk fel, és elvnek nevezzük azokat, ahelyett, hogy a mögöttes problémákra fizikai megoldásokat találnának.

A Pauli-féle kizárási elv hazugság. Inkább tesztként fogalmazzuk meg, hogy megmondja, mikor kell keresnünk fizikai különbségeket az egyébként azonosnak látszó részecskék vagy rezonanciák között.

53. hazugság A töltés belső

A fizikában a legnagyobb hazugságok közül az 53. a töltés sajátossága. A töltés a részecskék egyik legfontosabb tulajdonsága. A legjobban érthető és legalapvetőbb erő, az elektromosság és a mágnesesség az elektromos töltésnek köszönhető. A statikus töltés hatására a térben lévő dipólusok polarizálódnak, és elektromos mezőt képeznek. A mozgó töltések hatására a térben lévő dipólusok elfordulnak, és mágneses mezőt képeznek. A dipólusok csak azért léteznek, mert van töltés, és ugyanilyen fontos kétféle töltés, amelyeket pozitívként és negatívként határozunk meg.

Bármennyire is fontos a töltés fogalma az univerzum megértéséhez, fogalmunk sincs, hogy mi a töltés. Fogalmunk sincs, hogyan magyarázzuk el fizikailag, hogy mi a töltés. Mi a töltés? Nem tudjuk. Hogyan válnak töltéssé a részecskék? Nem tudjuk. Hogyan erednek a pozitív és a negatív töltések? Ezt sem tudjuk.

Mivel a fizikusok nem ismerik a töltést, hazárdíroznak, és a töltést belső részecsketulajdonságként kezelik. Csak ez megy náluk. Még Dirac is, amikor a nevét viselő egyenletet megfogalmazta, a töltést belső tulajdonságként kezelte, viszont egy elektron teljes egyenletében mind a töltést, mind a tömeget alaposabban kellene leírni.

A tömeghez hasonlóan (19. hazugság), az elektromos töltés belső tulajdonságként való kezelése a felelősség elengedése. A fizikusok feladata a fizikai tulajdonságok mélyebb megértése a fizikai megértés és a matematika segítségével. A töltés az elektromágneses elmélet alapja, tehát ha nem értjük, hogy mi a töltés, akkor nem értjük igazán az elektromágneses elméletet sem.

És bár több mint 122-féle részecsketömeg van, szerencsére amit meg kell magyarázni, csak két töltés: pozitív és negatív, azonos nagyságú, feltételezve, hogy a kvarkelmélet tört töltéseit figyelmen kívül hagyjuk. Így azt gondolhatnánk, hogy két töltést sokkal egyszerűbb kezelni.

Az egyik szempont, amely kihívást jelent a töltésrejtvényben az az, hogy a két stabil részecske, az elektron és a proton azonos, de ellentétes töltésű, de fizikailag eltérő méretűek és eltérő tömegűek. És akkor az antianyag ellentéteik is ugyanolyan nagyságúak, de ellentétesek. A töltés vagy független a mérettől, vagy egy konkrét szerkezeti problémához kötött megoldás, így csak ez a két méret stabil, ami valahogyan azonos töltési nagyságokhoz vezet.

Hogy elkerüljük ezeket a problémákat, és hogy egyáltalán fizikai magyarázatot adjunk, a fizikusok egyszerűen úgy döntöttek, hogy minden részecske pontszerű részecske, és ezeknek a pontszerű részecskéknek ponttöltésük van. A ponttöltés viszont egy másik hazugság a belső töltés hazugsága mellett.

A ponttöltés fogalmával a végtelenség a probléma. Tudjuk, hogy a részecske töltésének fix értéke van. Ha a részecske egy pont, más szóval végtelenül kicsi, akkor a töltéssűrűség is végtelen, feltéve, hogy a töltés osztható tulajdonság. A tömeghez hasonlóan a végtelen töltéssűrűséget sem tudjuk modellezni. Fizikailag nem lehet valós.

De meg is fordíthatjuk: ha van egy fizikai modellünk a töltésre, amely kisebb töltésegységekből áll, és ezt a modellt végtelenül kicsire vesszük, akkor két következtetésre jutunk. A töltés nulla lesz, vagy végtelenül nagy lesz az osztás nullával hiba miatt.

Voltak kísérletek a fizikai méretű részecskék töltésének fizikai modellezésére. A legelterjedtebb megközelítés az, hogy a töltés egyenletesen oszlik el egy felületen vagy térfogaton, végtelenül egyenletes módon, vagy számos kisebb töltési egységgel. Ez a töltés egyenlő egy csomó kisebb töltés megközelítő összegével. Ezek a közelítő töltésösszegek szintén nem foglalkoznak azzal a kérdéssel, hogy MI a töltés, vagy hogyan magyarázható fizikailag a töltés. Alapvetően azt mondják, hogy a töltés belső tulajdonság, de kisebb méretarányban.

Ahhoz, hogy jó fizikusok legyünk, és megtaláljuk a töltés fizikai magyarázatát, túl kell lépnünk a „töltés az töltés” fogalmakon, és inkább olyasmit kell keresnünk, ami nem töltés, hanem inkább egy fizikai jelenség, amely vonzást és taszítást okoz, töltést utánzó interakciókat. A töltés, mint a pozitív és negatív töltésenergia egyik formája az egyik lehetséges megközelítés. Egyelőre azonban nincs általánosan elfogadott magyarázat a töltés működésére.

Ebben a könyvben az összes hazugság közül talán ez a legspekulatívabb; mivel fennáll annak az esélye, hogy a töltés végső soron nagyon kevés valóban alapvető paraméter egyike lehet. De mivel említve volt, hogy az elektron és a proton töltése azonos nagyságú, és két egyedüli tartósan stabil részecske, véleményem szerint végül úgy találják, hogy ez egyetlen általános egyenlet két megoldása, ahol az elektromos töltés nagyságát a következőképpen írják le: valami más, mint a töltés. Matematikailag ez nagyon hasonlít az anyag és az antianyag megoldására a Dirac-egyenletben. Fizikailag és szerkezetileg, de ki tudja, így van-e?

A fizika sok más hazugságával ellentétben, bár bizonyos magabiztossággal kijelenthetjük, hogy a belső töltés elgondolása hazugság, és ellentétes a fizika tudományával, mégis nincs jó magyarázatunk arra, hogy mi az valójában. A töltés valódi természete tehát egy olyan kérdés, amely a fizikusok megoldandó tennivalói között marad.

54.Hazugság A pontszerű részecskék

A fizikában a legnagyobb hazugságok 54. része a pontrészecskék. A pontrészecske-probléma csak a intellektuális lustaságnak nevezhető dologból adódik. A fizikusok ahelyett, hogy a részecskék fizikai leírásával próbálkoznának, azt feltételezik, hogy a részecskék egy pontban léteznek, és minden tulajdonságuk belső.

A pontszerű részecskék tulajdonságaival kapcsolatos problémákat a 19., 20. és 53. számú hazugság tárgyalja a tömegre és a töltésre vonatkozóan. A ponttömeggel vagy ponttöltéssel kapcsolatos alapvető probléma a végtelen. A részecske tömege és töltése jól ismert értékeken van rögzítve. Ha a részecske egy pont lenne, más szóval végtelenül kicsi, akkor a tömeg vagy a töltéssűrűség végtelenül nagy lenne, feltételezve, hogy a tömeg és a töltés olyan tulajdonságok, amelyek oszthatóak. A végtelen tömeg vagy töltéssűrűség fizikailag nem lehet valóságos. Így a belső tömeg vagy töltés továbbosztott kisebb egységei sem lehetnek fizikailag valóságosak.

A tömeg azonnal megszakítja a pontszerű részecske modellt. Dirac feltételezte, hogy az elektron és a pozitron tömege a Dirac-tengerben egy lyuk, az éter fenntartásához szükséges energiának köszönhető. Ez nem csak az elektronok, hanem a protonok és neutronok esetében is helyesnek bizonyult, kísérletileg igazolható fizikai méreteik alapján. A rezonanciák tömegei némileg eltérőek, de látni fogjuk, hogy végső soron a nullaponti energia kizárásának is köszönhetőek.

Ha elképzelünk egy részecskét, amely sokkal kisebb, mint az ismert sugara, akkor az a kisebb, energikusabb vákuum-ingadozásokat kizárná, így tömege sokkal nagyobb lenne. Ha egy részecske akkora lenne, mint a Planck-hossz, akkor gyakorlatilag egy kis fekete lyuk lenne, hatalmas tömeggel. Ha egyszer elér egy valódi ponttömeghez, annak végtelenül nagynak vagy nullának kell lennie, de egyik válasz sem helyes.

Az elektromos töltéssel ugyanaz a probléma van, mint az előző fejezetben leírtakkal. Egy ponttöltés nulla lesz, vagy végtelenül nagy lesz a nullával osztás hiba miatt. Az elosztott töltésű részecskék nem lehetnek pontrészecskék, és az elosztott töltés nem tudja megmagyarázni, mi a töltés. Tehát a töltést más, jelenleg ismeretlen módon kell modellezni.

Az anyag és az antianyag olyan problémát jelent, mint az elektromos töltés, mivel a Dirac-egyenlet azt mutatja, hogy pozitív és negatív „energia” megoldások. Egy pontrészecskében a részecske anyagát vagy antianyag jellegét meghatározó „energiának” nullának vagy végtelennek kell lennie. Az elektromos töltéshez hasonlóan az anyagot és az antianyagot is másképp kell modellezni, valami fizikai dimenzióval és olyasvalamivel, ami nem oszlik el az anyag vagy az antianyag kisebb alegységei között.

A részecskék szögimpulzussal, mágneses mezővel és spinnel is rendelkeznek. Mindhárom tulajdonság azt is megköveteli, hogy a részecskék fizikai méretekkel rendelkezzenek ahhoz, hogy sikeresen modellezhessük őket. Egy pontnak nincs szögimpulzusa. Egy pont nem hozhat létre mágneses teret. Valójában nem tudjuk, mit jelent a spin, de lehetetlen, hogy a spin egy belső ponttulajdonság, mivel mérhető energiakülönbségekhez vezet.

A helyzet az, hogy a legtöbb fizikus látja ezeket a problémákat, mégis folyamatosan ismételgeti ezt a pontrészecske hazugságot. Úgy tűnik, hogy ez valóban az intellektuális lustaságuknak köszönhető, valamint annak képtelenségnek a beismerésének, hogy egyszerűen nem ismerik a részecskék szerkezetét. A fizikusok láthatóan inkább hazudnak, minthogy azt mondják: „nem tudjuk”.

55. hazugság: Kis elektronok

A fizikában a legnagyobb hazugságok 55. része a kis elektronok. A kicsi olyan elméletekre utal, amelyek egy pontrészecskéből eltérően helyezik el az elektron méretét, a Planck-hullámhossz méretét, 10-22 métert, 10-18 métert, 10-15 métert vagy bármilyen más fizikai átmérőt, amely kisebb, mint 10-12 méter. Az elektron sugara ismeretlen, mert az elektron szerkezete ismeretlen; bár egyes fizikusok odáig mennek, hogy azt mondják, nincs szerkezete. Általánosságban azonban elmondható, hogy a fizika főárama úgy gondolja, hogy egy elektron kisebb, mint 10-12 méter, ami a Compton-hullámhossznak felel meg.

A zűrzavar nagy része az elektronszerkezettel kapcsolatos feltételezésekből adódik. Amikor egy elektron modellezését próbálják megkísérelni, a fizikusok gyakran azt feltételezik, hogy az elektron tömegét kisebb tömegek, az egységnyi töltést pedig kisebb töltések összessége okozza. És akkor feltételezzük, hogy a mágneses momentum a kisebb töltések mozgásának köszönhető. A spint és más tulajdonságokat általában figyelmen kívül hagyják, míg a fizikusok ezekre az alapvető tulajdonságokra összpontosítanak. Az elosztott tömegeket és töltéseket ezután valamilyen módon megszervezték. A lehetséges szilárd geometriai objektumok, felületek vagy vonalak sokaságát próbálták ki, kezdve a legkézenfekvőbb gömb- vagy gömbhéj-modellekkel.

Az egyik legalapvetőbb érv a nagy elektronok ellen az, hogy ha egy elektron elosztott töltésekből áll, és a mágneses momentum ezek mozgásából adódik, akkor az elektron külső felületének meg kell haladnia a fénysebességet.

Ez a modell nem működik, ha feltételezzük, hogy a fénysebesség valóban korlátozza a forgási sebességet. Másrészt, ha a töltés nem oszlik el, hanem valami egészen más, akkor lehet, hogy nincs alapja annak, hogy a forgási sebességét a fénysebességre korlátozzuk, vagy nem szükséges, hogy túllépje a fénysebességet. Ahogy az lenni szokott, a fizikusok figyelmen kívül hagyták a nyilvánvaló alternatív választ. Az elektrontöltés nem a kisebb töltések összegyűjtéséből adódik. A töltés alapvető alapja valami más, mint a kisebb, de mégis belsőleg létező töltések.

Hasonlóképpen, az elektrontömeg nem a kisebb tömegek összegéből adódik. Mert ahogy Dirac is megjósolta, az elektron és a pozitron tömege az éterben való létezéshez szükséges energiának köszönhető. Ezek a részecskék egy bizonyos mennyiségű vákuumenergiát szorítanak ki. Ahhoz tehát, hogy Dirac hipotézise helyes legyen, számításaim szerint az elektron sugarának 1,6 x 10-12 méter körül kell lennie. Az elektron elektron tömege megköveteli, hogy sugara körülbelül fele akkora legyen a Compton-hullámhosszának. A Dirac elektrontömeg-modellje alapján a kisebb elektronok túl nagy tömegűek lennének, amint azt a 19. hazugság tárgyalja.

Sajnos a fizikusok nem végeztek foton- vagy elektronszórási kísérleteket egy Compton-méretű elektron méretének hivatalos meghatározására, így a pontos érték nem ismert. A fenti kísérleteket azért nem végzik el, mert a fizikusok úgy döntöttek, hogy a protonszórási kísérletek pontosabbak lennének. De ahelyett, hogy Compton-méretűek lettek volna, a protonszórási kísérletek sokkal kisebb méréseket eredményeztek. A protonszórási kísérletek alapján a fizikusok arra a következtetésre jutottak, hogy az elektronok sokkal kisebbek, mint a protonok, talán kevesebb, mint 10-18 méter, talán egy pont.

A fizikusok úgy döntöttek, hogy nem egyeztetik össze ezt a két nagymértékben eltérő mérést, de szigorúan ad hoc alapon úgy döntöttek, hogy a protonszórási kísérletek helyesek. Nem sikerült felismerniük, hogy a protonszórási kísérleteknek kétféle értelmezése van; az egyik az, hogy az elektronok kicsik, a másik az, hogy az elektronok átlátszóak a protonok számára. A fizikusok figyelmen kívül hagyták a második, kézenfekvőbb választ, amely életképes magyarázatot ad a tömegre.

A probléma másik része, hogy ha egy elektron nagy, a Compton-hullámhossz nagyságrendjében van, és átlátszó a protonok számára, az azt jelenti, hogy van szerkezete. És ha egy elektronnak van szerkezete, akkor talán nem elemi részecske, mivel bármiből is áll, annak eleminek kell lennie. Ne törődj azzal, hogy bármiből is készült, nem biztos, hogy létezik, kivéve, ha egy elektron vagy más részecske szerkezetében van. Ugyanez az érv szól a protonokról is, hogy nem lehetnek elemiek, mivel kimutatható szerkezettel rendelkeznek.

Egyelőre nincs bizonyíték arra, hogy bármi, ami elektronszerkezetet ad, létezik anélkül, hogy része lenne az elektronnak, kivéve a vákuum ingadozásait, amelyek az elektron belsejében laknak. De kiterjesztve, ha az elektronoknak van szerkezete, akkor a virtuális elektronoknak és a pozitronoknak hasonló szerkezettel kell rendelkezniük. Azt azonban nem tudjuk, hogy miből állnak, és bármi legyen is az, nem jelenik meg ezektől a virtuális részecskéktől függetlenül. Az eddigi bizonyítékok alapján csak azt feltételezhetjük, hogy bármi is alkotja az elektron szerkezetét, az csak egy elektron részeként, és esetleg más, hasonló részecskék részeként fordul elő.

A kis elektron-elméletek hazugságok. A továbblépés a Compton-méretű elektronok fizikai szerkezetének megismerése a szórási kísérletekkel, mivel az elektron tömege ennek a fizikai dimenziónak köszönhetően fizikai tulajdonság.

56. hazugság: Az elektronok és a protonok között nincs taszító erő

A fizikában a legnagyobb hazugságok 56. pontja az, hogy nincs taszító erő az elektronok és a protonok között. A fizika standard modelljében az egyetlen erő az elektronok és a protonok között a coulomb-vonzás. Ez az alapvető elektromos vonzás, amely abból adódik, hogy a proton pozitív, az elektron pedig negatív töltésű.

A standard modellben nincs taszító erő az elektronok és a protonok között. De ha valóban nem lenne taszító erő az elektronok és a protonok között, akkor az elektronok a Coulomb-vonzás következtében protonokba hullanának, és neutronokat képeznének. Így nem lenne hidrogén az univerzumban.

Kísérletileg tudjuk, hogy amikor az elektronok közel kerülnek a protonokhoz, akkor taszítóerő lép fel, amelyet körülbelül 780 keV (kilo-elektron-volt) energiával mértek. Összehasonlításképpen egy elektron tömegenergiája 511 keV, tehát ez a potenciálgát óriási mennyiségű energiát képvisel a részecskeskálán. Ez nem elhanyagolható dolog, vagy olyan dolog, amelyet könnyen el kell vetni, és a szabványos modellfizikusok azonban figyelmen kívül hagyják az erőelméletek mérlegelésekor.

Ez a potenciális gátenergia megakadályozza, hogy az elektronok egyszerűen a protonokba essenek, de a fizikusok meg sem próbálják meghatározni ennek az erőnek a természetét. Ehelyett egy hullámegyenletet használnak az atom energiaállapotainak leírására, és figyelmen kívül hagyják, hogy van egy erő, amely kiegyensúlyozhatja az egyenleteiket.

Tehát most módosítanunk kell az alapvető erők listáját.

Ezek:

1. mechanikai erő,

2. elektromágneses erő,

3. gyenge erő,

4. erős erő,

5. sötét erő,

6. nagy energiájú gravitációs erő,

7. taszítóerő elektronok és protonok között.

Az alapvető erők listája azonban kezd túl bonyolulttá válni, ezért egyszerű módot kell találni annak egyszerűsítésére. Az elektronok és protonok közötti taszító erő két anyagrészecske közötti taszító erő, tehát olyan erőt jelent, amely az anyagot taszítja az anyagtól. A sötét erő egyben olyan erő is, amely az anyagot az anyag által taszítja. Ezenkívül a mechanikai erő hatására az anyag taszítja az anyagot.

Ezzel szemben az anyagot nagyon közelről vonzza az antianyag. Érdekes lenne pozitronokat lőni a protonokra, és megnézni, hogy ez mérhető-e. Azonban a két pozitív töltésű részecske közötti coulomb taszítás uralja a kölcsönhatást normál távolságokban.

Az a hazugság, hogy az elektronok és a protonok között nincs taszító erő, valóban a fizika egyik legnagyobb hazugsága. Ez egy hazugság, amely erősen korlátozta a fizika fejlődését az elmúlt 90 évben, mivel a fizikusok folyamatosan nem vették észre, hogy elméleteikből hiányzik egy erő.

57. hazugság: A Schrödinger-egyenlet az elektronok mozgását írja le

A nullponti energia következménye az volt, hogy egy stacionárius atomállapotban lévő elektron nem mozog spirálisan az atommagba, ha olyan sebességgel nyeli el a nullponti energiát, amely kiegyenlíti az energiasugárzás sebességét. Csak akkor sugárzik, ha az utóbbi meghaladja az előbbit. A nullponti sugárzás valójában lehetővé teszi az alapállapot fogalmát, amelyből nem következik be további bomlás. 69

Peter Finley Browne, 1995

A fizikában az 57. legnagyobb hazugság a Schrödinger-egyenlet, amely leírja az elektronok mozgását. A Schrödinger-egyenlet Erwin Schrödinger által kidolgozott hullámegyenlet a hidrogénatom atommagja körüli elektronok energiaállapotainak magyarázatára. A fejlesztés célja a Bohr-modell nehézségeinek orvoslása volt. Azóta más rendszerekre is kiterjesztették, és széles körben a kvantummechanika egyik legfontosabb egyenletének tartják.

A Schrödinger-egyenlet alapvető magyarázatot ad az elektronállapotok kvantálására, amelyeket általában pályáknak neveznek, bár ezeket nem a klasszikus értelemben vett pályáknak, hanem energiaállapotoknak kell tekinteni. Azt is gondolták, hogy a hullámegyenlet megoldotta azt a problémát, hogy az elektron nem sugároz ki fotonokat, miközben irányt változtat a pályáján, ahogyan azt a klasszikus elmélet szerint az elektronok teszik.

Noha a Schrödinger-egyenlet kétségtelenül nagyon sikeres, nem ad választ bizonyos alapvető kérdésekre az elektronok mozgásával kapcsolatban.

A Nem magyarázza meg, hogy az elektromos erő hatására felgyorsított elektron, amely közvetlenül a proton felé halad, hogyan nem esik a protonba.

B. Nem magyarázza meg, hogy egy közvetlenül a proton felé mozgó elektron hogyan változtatna irányt, és hogyan kezd el „keringeni” a proton körül a hullámegyenletnek megfelelő módon.

C. Nem tartalmazza az elektron és a proton közötti taszító erőt.

D. Valójában nem magyarázza meg, hogy az elektron hogyan nem sugároz ki fotonokat mozgás közben, a fizikai mechanizmus biztosítása szempontjából.

E. Ismeretes, hogy az elektronok felhőnek tűnő kvantumállapotot foglalnak el, miközben egyik helyről a másikra ugrálnak a felhőn belül. Az egyenlet nem írja le ezt az ugró mozgást.

F. Minden elektronfelhő egy sor távolságot tartalmaz az atommagtól, tehát klasszikus értelemben minden ugrás kis energiaváltozást tartalmaz, miközben nem sugárzik. Ez nincs megmagyarázva.

G. Az elektronok egyik pályaállapotból a másikba ugrálnak anélkül, hogy gyorsítanák, lassítanák vagy elfoglalnák a közbenső teret, ami megsérti a fizika klasszikus elveit. Ez nincs megmagyarázva.

H. Ezeket a pályaugrásokat egy foton emissziója vagy abszorpciója kíséri, attól függően, hogy az energiaállapot csökken vagy növekszik. Ezeket a foton-kölcsönhatásokat nem magyarázza meg a hullámegyenlet. Vegye figyelembe, hogy ezt a következő fejezetben fogjuk megvizsgálni.

I. Nem magyarázza meg fizikai értelemben, hogy az elektronok hogyan nem foglalnak el azonos kvantumállapotokat. A Pauli-féle kizárási elv végül is egy szabályalapú megközelítés, amely nem tartalmaz fizikai mechanizmust. Mint ilyen, tehát hiányos.

Az első három A, B és C pont azt mondja nekünk, hogy szükség van egy erőkiegyenlítő egyenletre, amely magában foglalja a proton és az elektron közötti ~780 keV taszítópotenciált. Ha ezt az erőt be lehetne építeni egy hullámegyenletbe, az még jobb lenne. D-től H-ig azt mondja nekünk, hogy hiányzik valamilyen fizikai mechanizmus a kvantummodelleinkből, és rámutatok egy másik fizikai mechanizmusra vagy erőre, amely hiányzik a modelleinkből.

A D-től H-ig terjedő kérdések szerencsére könnyen megmagyarázhatók, ha felismerjük, hogy az atom belsejében lévő tér még mindig tele van virtuális elektron-pozitron párokkal, és a virtuális pozitronok megsemmisülhetnek és meg is teszik a szabad elektronokkal. Tehát amikor egy virtuális pozitron túl közel kerül egy szabad elektronhoz, megsemmisítik egymást. Ez a megsemmisülés szabadon hagyja a virtuális elektront, hogy örökölje a megsemmisült szabad elektron kvantumállapotát. Ez a mechanizmus olyan, mint a Hawking-sugárzás, de ahelyett, hogy egy virtuális részecskét elfogna egy fekete lyuk, amely megsemmisítené. Ezt az 57-1. ábra szemlélteti.

57-1. ábra Egy alapvető vákuumfluktuáció által közvetített annihilációs-termelési esemény, ahol egy szabad elektron megsemmisül, és az egyszeri virtuális elektron veszi át a helyét.

Ez a fajta megsemmisítés-előállítási mechanizmus egyszerű és elegáns, és ami fontos, semmi sem tiltja, hogy megtörténjen. Bátran kijelenthetjük, hogy ilyen interakcióknak meg kell történniük.

Ezek a kölcsönhatások világos fizikai modellt adnak nekünk arra vonatkozóan, hogyan ugrálnak az elektronok az elektronfelhőn belül. Az egyetlen kvantumállapoton belüli kisebb energiaváltozásokat a vákuumból származó vagy a vákuumba visszavezetett kis mennyiségű energia magyarázza. Ebből a szempontból az elektront úgy tekinthetjük, mint amely egyensúlyban van a nullponti mezőkkel, ahogy Browne a fenti idézetben kifejti, ami Planck és Nernst munkáiból származó ötlet volt. 69 Ez gondoskodik D-től F-ig.

Ami az orbitális átmeneteket illeti, láthatjuk, hogyan működnek ott a megsemmisülés-megjelenés kölcsönhatásai, ahogy ezt az 57-2. ábra szemlélteti. De ebben az esetben az elektron energiaállapota megváltozik, ezért a kölcsönhatásban egy fotonnak is részt kell vennie. Ha az elektron alacsonyabb energiájú, akkor alacsonyabb pályaállapotba ugrik, akkor egy foton keletkezik, amely ekkora energiát bocsát ki. Ahhoz, hogy egy elektron magasabb energiájú állapotba ugorjon át, el kell nyelnie egy fotont. Ez gondoskodik G-ről és H egy részéről.

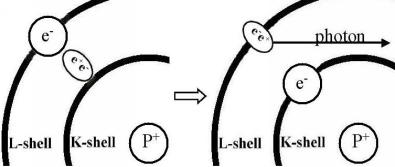
57-2. ábra Egy Bohr-féle hidrogénmodell, amely egy elektron-pozitron vákuum fluktuáció által közvetített elektronpálya-átmenetet mutat foton emissziójával.

Ez csak egy kis mintája azoknak a kölcsönhatásoknak, amelyek nullponti energiadipólusokkal való megsemmisülési-megjelenési kölcsönhatásokon keresztül valósulnak meg. Minden kvantumugrás típusú mozgás a kvantumskálán végül így történik. Testünkben minden részecske folyamatosan megsemmisül és újratermelődik, ahogy haladunk az űrben. A részletesebb megbeszélésekért tekintse meg a Kvantumugrások mint vákuum-fluktuációs részecskepár kölcsönhatások Hawking-sugárzással analóg cikkemet. 71

Ami az utolsó, kilencedik I. problémát illeti, ezt a Pauli-féle kizárási elv egy másik hipotetikus következményének is tekinthetjük, ez pedig a degenerációs nyomás. Úgy gondolják, hogy ez az elv nemcsak azt akadályozza meg, hogy két elektron ugyanabban az állapotban legyen, hanem összenyomóerőhöz is vezethet. Úgy gondolják, hogy ez az erő fontos a fehér törpe csillagok fejlődéséhez.

Ez valójában azt sugallja, hogy az elektronok között taszító erő van. Mivel a Pauli-féle kizárási elv nem alapvető erő, ez egy újfajta erő. Fontos megjegyezni azt is, hogy a Pauli-kizárási elv nem tehető felelőssé az elektronok és protonok közötti erőért, mivel a különböző részecskék között nem érvényesül. A kvantummechanikai hullámegyenleteknek ezt az erőt is figyelembe kell venniük.

Ez újabb erőt ad a listánkhoz. Azaz:

1. mechanikai erő,

2. elektromágneses erő,

3. gyenge erő,

4. erős erő,

5. sötét erő,

6. nagy energiájú gravitációs erő,

7. taszító erő az elektronok és a protonok között,

8. taszító erő az elektronok között.

Az az állítás, hogy a Schrödinger-egyenlet az elektronok mozgását írja le, hazugság. Listánkból láthatjuk, hogy számos olyan hiányosság van az elméletben, amelyek csak új fizikai magyarázatok bevezetésével oldhatók meg.

P.F. Browne, „The Cosmological Views of Nernst: An Appraisal”, Apeiron, Vol. 2 N. 3, 1995. július.

70 E. Schrödinger, E., "An Undulatory Theory of the Mechanics of Atoms and Molecules". Fizikai áttekintés. 28 (6): 1049–1070, 1926.

71 R. Fleming, „A kvantumugrások, mint a Hawking-sugárzással analóg vákuumfluktuációs részecskepár kölcsönhatások”

https://gsjournal.net/Science-Journals/Research%20Papers-Quantum%20Theory%20/%20Particle%20Physics/671Download

58. hazugság: A fizika megmagyarázza a foton-kibocsátást

A fizikában az 58. legnagyobb hazugság az, hogy a fizika megmagyarázza a foton-kibocsátást. A foton-kibocsátás és abszorpció a fizika két legfontosabb kölcsönhatása, és jóllehet a fizikusok azt gondolhatják, hogy tudják, hogyan és mikor keletkeznek a fotonok, erre nincs elfogadott fizikai magyarázat.

Az utolsó fejezetben láttuk, hogy Browne Planck és Nernst munkái alapján arra a következtetésre jutott, hogy stabil, nem sugárzó pályák jöhetnek létre, ha az elektront a nullponti mezővel való kölcsönhatások stabilizálják. 69 Vegye figyelembe, hogy a virtuális elektron-pozitron párok fénysebességgel forognak anélkül, hogy kisugároznának.

Érdekes módon valójában nem látjuk, hogy a részecskék fotonokat sugároznak, amikor keringenek vagy ívelt pályákon haladnak, amikor elektromos vagy mágneses mezők befolyásolják őket. Ez a klasszikus feltételezés a kísérleti adatok hiánya alapján hamisnak tűnik. Hazugság az az állítás, hogy a pályán vagy görbe úton haladó részecskéknek fotonokat kell sugározniuk. Ehelyett olyan helyzet áll előttünk, amikor a részecskék egyensúlyban vannak az éterrel, így nem kell kisugározniuk. Amikor látjuk a foton-kisugárzást, éles irányváltás történik.

Az elektronok és a virtuális elektron-pozitron párok közötti megsemmisülési-teremtési kölcsönhatások olyan fizikai modellt adnak számunkra, amely lehetővé teszi számunkra, hogy megértsük, hogyan mozognak, vagy különösen ugrálnak az elektronok foton kibocsátása nélkül. Amikor ez megtörténik, az elektron valóban egyensúlyban van a nullponti mezővel, és nem sugárzik.

Az előző fejezet 57-2. ábrája modellt ad a fotonok kibocsátására a pályaátmenetek során. Amikor egy elektron és pozitron megsemmisül, miközben energiája nem nulla, új fotont indítanak el. Mivel egy foton virtuális elektron-pozitron párok sorozatából áll, logikus, hogy egy foton ugyanúgy indul ki, egy elektron-pozitron pár megsemmisülésével.

Hipotetikusan egy foton kezdődhet bármely, nem nulla energiájú valós részecskepár, például egy proton-antiproton pár megsemmisítésével. Egy ilyen proton-antiproton foton felelős lehet bizonyos nagyon nagy energiájú fotonokért.

58-1. ábra Bohr-típusú hidrogénmodell, amely egy fotonból származó virtuális elektron-pozitront mutat be, mely kölcsönhatásba lép egy pályaelektronnal, és magasabb pályára ugrást okoz.

Az elektronpálya-átmenetet fordítva is meg lehet nézni, hogy megmagyarázzuk a fotonabszorpciót. Amikor egy foton nekiütközik egy pályaelektronnak, akkor elnyelheti, ha rendelkezik megfelelő energiával ahhoz, hogy az elektron magasabb pályára ugorjon, vagy teljesen kilökjön a pályáról. Természetesen az ugrás ebben az esetben egy virtuális elektron-pozitron által közvetített annihilációs kölcsönhatás, de ebben az esetben az elektron és a pozitron a fotonból származik a nullponti mező helyett. Egy ilyen interakció kezdetét az 58-1. ábra szemlélteti.

A fekete test sugárzása egy másik fontos példa. Nem tudjuk kitalálni, hogyan bocsátódik ki a CMB vagy bármely más fekete test sugárzása, ha nem értjük, hogyan keletkeznek a fekete test fotonjai. Ha megértjük, hogy a virtuális részecskepárok elindítják a folyamatot, könnyen kitaláljuk a többit.

Az anyagtestben lévő termikus elektronok energiája a test hőmérsékletéhez viszonyítva van. Amikor egy virtuális elektron-pozitron pár túl közel kerül, a pozitron megsemmisül, és az elektron olyan fotont hoz létre, amely magában foglalja az elektron hőenergiájának egy részét vagy egészét. Az egyszer virtuális elektron szabaddá válik, és magával viszi a maradék energiát. Az éter kisugárzásához szükség lenne a vákuum-ingadozások közötti kereszt-megsemmisítésre, amikor az egyik vagy mindkét vákuum-ingadozás valamilyen módon többletenergiára tett szert, talán a van der Waals-kölcsönhatások miatt.

Nagyon világosan fel kell ismerni, hogy azok a fizikusok tévednek, akik azt hiszik, hogy a standard modell megmagyarázza azt, hogy hogyan keletkeznek és abszorbeálnak a fotonok. Ha megértjük, hogy a vákuumot részecskepár-dipólusok töltik ki, és a fotonok részecskepár-dipólusok, akkor egyszerűvé válik a fotontermelés és -abszorpció fizikai magyarázata.

Hazugság azt állítani, hogy a fizika megmagyarázza a fotontermelést a virtuális részecskepár megsemmisülés-termelés modell helyett.

59. hazugság: A semleges pion kvark modell

Ha a h-sor alapvető, akkor e-t valamilyen módon a h-sáv négyzetgyökével kell megmagyarázni, és a legvalószínűtlenebbnek tűnik, hogy bármely alapvető elmélet megadja e-t négyzetgyökben, mivel a négyzetgyökök ezt teszik. nem fordul elő az alapegyenletekben. 72

Paul Dirac, 1963

A fizika legnagyobb hazugságai közül az 59. a semleges pion kvark modell.

A semleges pion fontos a fizika számára, mivel ez a legelemibb metastabil részecskék vagy rezonanciák. Rövid élettartamuk miatt metastabilnak tekinthetők, ami 8,4 x 10-17 másodperc nagyságrendű. Ez még mindig hosszú idő egy olyan részecskénél, amely nem tartósan stabil, összehasonlítva más instabil részecskékkel, amelyek mindegyike még rövidebb élettartamú.

A semleges pionok valójában egyáltalán nem részecskék, hanem valami más rezonanciaállapota, ahol ez a valami egy másik részecske vagy részecskék kombinációja. Az 1960-as években még gyakori volt, hogy a fizikusok nyitva hagyták azt a kérdést, hogy egy rövid élettartamú részecske részecske-e vagy csak rezonancia, de mivel a Nobel-díjat könnyebben odaítélik a részecskék felfedezéséért, mint a rezonanciákért, a fizikusok már nem nevezték rezonanciáknak. Ez szégyen, mert kitalálhatjuk, hogyan származtathatunk 122+ különböző tömeget egy rezonanciamodell részeként, de nem egy részecskemodellből.

Ha egy részecske rezonancia, akkor az összetételének meghatározásának első módja annak megvizsgálása, hogy mivé bomlik. A semleges pion általános bomlási útvonalai a következők:

1. két foton,

2. egy elektron és pozitron,

3. egy foton plusz egy elektron-pozitron pár,

4. két elektron-pozitron pár.

Tehát a bomlási utakból a pion modellezésének legegyszerűbb módja az lenne, ha abból a feltevésből indulnánk ki, hogy egy elektron-pozitron párról van szó valamilyen metastabil állapotban. Egy elektron-pozitron pár ezután kölcsönhatásba léphet egy virtuális elektron-pozitron párral, hogy létrehozza mind a négy lehetséges bomlásterméket.

De ehelyett a fizikusok átvették a kvark modellt, és a kvark modellen belül a semleges pion valami egészen mással egyenlő. Ennek az egyenletnek a jobb oldala az alábbi ábrán látható.

59-1 ábra

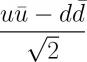
A kvark modellben a semleges pion egy lefelé és egy anti-le kvark párból áll, amelyet le kell vonni egy felfelé és anti-felfelé irányuló kvark párból, osztva 2 négyzetgyökével. Ez a képlet néhány kulcskérdést vet fel.

A. Amikor egy kvark és antirészecskéje együtt megsemmisül, nem hagy mást, csak energiát és lendületet?

B. Ha az elemi részecske-anti-részecske pár megsemmisülésekor az energián és a lendületen kívül marad valami, akkor azok valójában elemiek?

C. Ha egy elemi részecske kivonható egy másik elemi részecskéből, így valami nettó különbség marad, akkor valóban elemi részecskéknek tekinthetők?

D. Ha egy elemi részecske osztható kettő négyzetgyökével, valóban lehet elemi?

E. Ha egy részecskeegyenlet osztható négyzetgyökkel, akkor irracionális?

Az első két kérdésre a válasz igen és nem. Lényegében a képlet úgy van kitalálva, hogy két foton legyen a bomlási termék, de ez a kvarkkombináció nem lehet részecske, még csak rövid életű sem. Természetesen az alapvető részecskék sem vonhatók ki egymástól.

Ahogy Paul Dirac kifejtette, ha valami osztható négyzetgyökkel, az valószínűleg nem alapvető. A semleges pion kvark modellje valóban irracionális mind nyelvi, mind matematikai értelemben.

Kiderült, hogy Ernest Sternglass 1961-ben felfedezett egy alternatív elméletet. 73 Sternglasst Enrico Fermi és Chen-ning Yang korábbi kísérlete után ihlette meg, hogy összetett modellt keressen a pion számára. 74,75 Richard Feynman némely szorongatásával felismerte, hogy a semleges pion relativisztikus elektron-pozitron párként modellezhető. Rezonáns pionmodelljében egy elektron-pozitron pár a fénysebességhez közeli sebességgel, relativisztikus sebességgel forog. Ez a fajta modell teszi lehetővé számunkra, hogy ténylegesen leegyszerűsítsük a részecskeelméletet, és megmagyarázzuk a 122+ különböző tömeget.

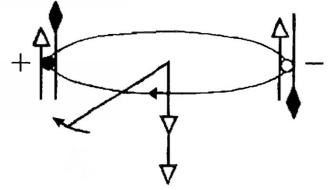
59-1. ábra Sternglass stílusú illusztráció egy semleges pionról egy elektron-pozitron párral, amelyek egymás körül keringenek. A nyitott nyilak a szögimpulzust, a tömör nyilak pedig a mágneses momentumokat jelölik.

Sternglass felfedezésének zsenialitása két részből állt. Rájött, hogy amikor az egyik részecske forog a másik körül, egy centrifugális erő húzza el a kifelé irányuló részecskét, és ha ez az erő egyenlő a részecskéket összehúzó elektrosztatikus vonzó erővel, akkor metastabil pályájuk van. A második rész az volt, hogy míg van egy ilyen alacsony energiájú metastabil állapot, amit pozitróniumnak neveznek, addig van egy második relativisztikus metastabil állapot is. Valójában Feynman megérdemli az elismerést ezért az ötletért, Sternglass feljegyzései alapján. 74 Ahogy Sternglass elmeséli a történetet, a részleteket dolgozta ki egy táblán Feynman előtt, amikor egy egyszerű pályaképlet segítségével származtatta a pion tömegét, mint amilyet Bohr használt a hidrogén kvantumállapotainak felfedezésekor. Később levezette a felezési időt.

A mainstream fizikusok, nevezetesen Alfred Schild, „megcáfolták” a pion-modellt, kijelentve, hogy nem létezik relativisztikus elektron-pozitron páros megoldás, noha ismert, hogy a vákuumfluktuációs részecskepárok relativisztikus sebességgel forognak. Schild arra a következtetésre jutott, hogy az elektronpár relativisztikus tömegenergiájának kisebbnek kell lennie a nyugalmi tömegénél. 76 Következtetése egyértelműen téves, mivel a relativisztikus sebességgel mozgó részecske teljes relativisztikus tömegenergiája mindig nagyobb, mint a részecske nyugalmi tömege.

A fizikusokat megzavarta a Sternglass modell, és az elektronokat és a pozitront szabad részecskéknek látták. Nem sikerült felismerniük, hogy ebben a modellben a pion virtuális elektron-pozitron párok metastabil sorozata. Továbbra is panaszkodnak, hogy relativisztikus elektron-pozitron pár nem létezhet, teljesen figyelmen kívül hagyva azt a tényt, hogy a virtuális elektron-pozitron vákuum-ingadozások folyamatosan a fénysebességet is beleértve. A kvantumtérelmélet azt mondja, hogy léteznek relativisztikus elektron-pozitron párok. Az, hogy a fizikusok nem tudják kielégítően modellezni őket, az a probléma velük, és nem a Sternglass-elmélet.

Egy másik probléma, hogy Sternglass egy Bohr-típusú modellt használt, amely a fizikusok szerint nem elég kifinomult, mivel nem oldja meg a fotonsugárzás szükségességét, ha egy részecske körpályán áll. Azt mondták, hogy ezt hullámegyenletként kell kiszámítani, és nem vették észre, hogy a hullámok a nullapont mező sajátosságai, nem pedig a részecskéké. Míg a Sternglass pion modell javítható és kifinomultabbá tehető, ez nem teszi érvénytelenné a koncepció bizonyítását. Ahogy az előző fejezetben tárgyaltuk, az ívelt pályát követő részecskék nem sugároznak ki fotonokat, így panaszuk egy része helytelen.

Tehát a fizikusok nemcsak feltalálták a semleges pion fiktív modelljét, hanem figyelmen kívül hagytak egy sikeresebbet is. A Sternglass-modell összhangban van azzal, hogy az éter virtuális elektron-pozitron párokból áll, mivel a pionok egyszerűen létrehozhatók, ha egy virtuális elektron-pozitron pár elegendő energiát kap ahhoz, hogy felvegye a metastabil semleges pion rezonancia állapotot.

Végül egyszerűen szükségünk van erre a modellre, vagy talán egy kicsit más modellre ilyen egyszerűséggel, hogy képesek legyünk modellezni az összes részecskét és rezonanciát. Végső soron 122+ különböző tömeget kell levezetnünk az alapelvekből.

A semleges pion kvark modell valóban a fizika egyik legnagyobb hazugsága

72 P.A. Dirac, „The Evolution of the Physicist's Picture of Nature”, Scientific American, 1963. május, 208(5), 45-53.

73 E. J. Sternglass, „Relativisztikus elektronpár rendszerek és a semleges mezon szerkezete”, Phys. Rev., 123, 391, 1961.

74 E. J. Sternglass, A Cornell Egyetem Kroch Könyvtárának Ernest J. Sternglass gyűjteményében található részecskefüzetekből.

75 E. Fermi C.N. Yang: „A mezonok elemi részecskék?” Phys. Rev. 76, 1739, 15, 1949 dec.

76. A. Schild, “Electromagnetic two-body problem,” Phys. Rev., 131, 2762 1963.

60. hazugság: A többi irracionális Mezon-modell

A fizika legnagyobb hazugságai közül a 60. a többi irracionális mezon-modell. A mezonok köztes részecskék vagy rezonanciák tömegekkel, amelyek az elektron és a proton közé esnek. Az 59. hazugságban leírt semleges pionhoz hasonlóan van 6 másik mezon is, amelyek hasonlóan irracionálisak. A kvark modell hatókörén belül az eta mezonok 8 kvarkból állnak, osztva 6 négyzetgyökével, a 60-1. ábrán látható matematikai összefüggéssel.

60-1. ábra

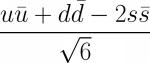
Az Eta prím-mezonok állítólag 6 kvarkból állnak, osztva 3 négyzetgyökével, a 60-2. ábrán látható matematikai összefüggéssel.

60-2. ábra

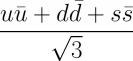
A K-rövid mezonoknak 2 egymást kiegészítő kvarkpárból kell állniuk, amelyeket kivonnak egymástól és osztanak el 2 négyzetgyökével, a 60-3. ábrán látható matematikai összefüggéssel.

60-3. ábra

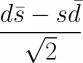
A K hosszúságú mezonoknak 2 komplementer részecskepárból kell állniuk, de ezúttal összeadjuk, majd elosztjuk 2 négyzetgyökével a 60-4. ábrán látható matematikai összefüggéssel.

60-4. ábra

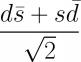
A semleges rho mezonok ugyanazokkal az összetevőkkel rendelkeznek, mint a semleges pion, de állítólag különböznek a piontól, beleértve a nagyobb tömeget és rövidebb felezési időt. Lásd a 60-5. ábrát.

60-5. ábra

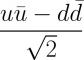
Az omega mezonok olyanok, mint a semleges rho vagy pion, kivéve, hogy a kvark párokat valahogy hozzáadják ahelyett, hogy kivonnák őket, ahogy az a 60-6. ábrán látható.

60-6. ábra

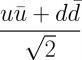
Mindezek a matematikailag irracionális mezonmodellek irodalmi értelemben is irracionálisak. A semleges pionhoz hasonlóan a megsemmisült részecske-antirészecske párokból még metastabil részecskét sem lehet előállítani. Ezen túlmenően ezek a párok fizikailag nem vonhatók ki egymástól és a kvarkok, ha mind fizikailag valósak, mind elemiek, nem oszthatók egy egész szám négyzetgyökével.

A K-short és K-long egy újabb dimenziót ad az irracionalitásnak. A down-kvark és az anti-furcsa-kvark egyenértékű a kaon mezonnal. Egy furcsa-kvark és egy anti-down-kvark akkor anti-kaon lesz. Tehát ha hozzáadunk egy kaont és anti-kaont, akkor megsemmisülnek, és nem lesz semmi utána, még ha túlzott energiára és lendületre is számítanak. És a kaonok szintén nem oszthatók 2 négyzetgyökével.

A kvark modell keretein belül, beleértve a semleges piont is, 7 mezon van ilyen irracionális módon modellezve. Ezek a többi mezonmodell együttesen a fizika egyik legnagyobb hazugsága. Ezek nem ezek az ismert rezonanciák fizikai leírásai.

Ebből következik a kérdés, hogy ha ezek a mezonok nem kvarkokból állnak, akkor miből? Kiderült, hogy a részecskék tömegei, mind a mezonok, mind a nehezebb hadronok olyan értékekkel állnak kapcsolatban egymással, amelyek közel állnak a finomszerkezeti állandó inverzének, a ~137-nek a többszöröséhez. Ennélfogva némi finomhangolással az elektronon, protonon és neutronon kívül minden részecskét/rezonanciát lehet modellezni egy vagy több elektron-pozitron pár használatával. Ha az elektron és a proton bomlási termék, akkor ezek is a modell részét képezik. Tehát ezek a részecskék elektron-pozitronpárok gerjesztett állapotaként modellezhetők a Sternglass pion modellel összhangban.

Ne feledje, hogy ebben a szakaszban a Sternglass modellt útmutatónak kell tekinteni a megvalósításának a módjához, de nem szükséges útmutatónak a dolgok alakulásához. A modellje némi egyszerűsítést igényelhet. Ennek ellenére érdemes áttekinteni, de a hely korlátai miatt itt nem foglalkozunk vele részletesebben. További információkért tekintse meg a Sternglass dokumentumait. 77,78

77 E. J. Sternglass, „Electron-positron model for the charged mezons and pion resonances”, Il Nuovo Cimento, 1 Gennaio, Volume 35, Issue 1, pp. 227-260 (1965)

78 E. J. Sternglass, „Új bizonyítékok a mezon- és barionrezonanciaállapotok molekuláris szerkezetére”, Proceedings 2nd topical Conference on Resonant Particles, 33-53. o., 1965.

61. hazugság: A kvarkok

Ne’eman: Kérdezhetek valamit, amit Feynman kérdezett tőlem valamikor: Készen állna-e elvetni az elméletét, ha kiderül, hogy a 720-as mezon spinje 0 és nem 2, vagy ha van ott egy másik nukleonállapot?

Sternglass: Egy ilyen elméletnek vagy minden részecskére igaznak kell lennie, vagy egyáltalán nem jó.

Ne’eman: Ez minden bizonnyal kielégítő válasz. 79

Yuval Ne’eman és Ernest Sternglass, 1965

A fizika legnagyobb hazugságai közül a 61. a kvarkok. A fenti eszmecsere Yuval Ne'eman és Ernest Sternglass között az Ohio Egyetemen, 1965 júniusában, a rezonáns részecskékkel foglalkozó második témakonferencián történt. A kvark modell az előző évben jelent meg, és Ne'eman Murray Gell-Mannnal együtt önállóan fejlesztette ki. a numerológiai szimmetriaelmélet, amely a kvarkelmélethez vezetett. Mint ilyen, Ne’eman erősen rábízta magát a kvarkelméletre, és a konferencián Sternglass elméletét támadta. A sors úgy döntött, hogy a kvark modellnek kell megfelelően figyelembe vennie az egyes mezonok tulajdonságait. "Egy ilyen elméletnek (azaz a kvark modellnek) vagy minden részecskére igaznak kell lennie, vagy egyáltalán nem jó."

Az igazat megvallva, a Sternglass modellt soha nem fejlesztették ki teljesen, így hiányosságok vannak abban, hogy mit takar, és némi egyszerűsítést alkalmazhat a fizikai felépítését illetően. Ennek ellenére nagy különbség van egy nagyrészt sikeres elmélet között, amely folyamatban van, és egy jól kidolgozott elmélet között, amely helyenként nyilvánvalóan téves, és nem tudja megmagyarázni a legelemibb rezonanciákat.

A legalapvetőbb mezon a semleges pion; tehát ahhoz, hogy érvényes fizikai modellünk legyen a mezonokra és általában az összes részecskére/rezonanciára, egy érvényes modellel kell kezdenünk a semleges pionra. A mezonok modellezésének rendszere a semleges pionnal kezdődik, és az összes többi mezon modellnek ezen kell alapulnia.

Ha a pion modelled hazugság, amit a kvark pion modell az 59. hazugságban kifejtett, akkor az egész részecskemodell hazugság. Természetesen a 60. hazugságban tárgyalt 6 másik irracionális mezonmodell csak megerősíti azt a tényt, hogy a kvark modell nem teljesíti a Feynman-tesztet.

Néhányan azt gondolhatják, hogy „a kvarkok létezését kísérletileg igazolták”, de ez nem igaz. Kvarkokat még soha nem láttak a laboratóriumban. Létezésükre csak következtetni lehet. Amilyen mértékben létezik valami, amit kvarknak értelmeztek, az csupán egy rezonancia, amely valami hosszabb élettartamúvá bomlott, amit észlelhetünk. A kvarkként átadott rezonanciák csak más részecskék kombinációinak rezonáns állapotai, ha egyáltalán vannak ilyenek.

Végső soron meg kell találnunk egy részecskeelméletet, ami sokkal egyszerűbb, mint a kvarkelmélet. Muszáj, mert egy olyan modell, amely 122+ részecskékhez 122+ belső tömeget igényel, nem alapvető elmélet. Mivel a tér vákuumában számos virtuális elektron-pozitron pár található, ésszerű olyan részecskeelméletet építeni, amelyben az összes rezonancia alapegységei az elektron-pozitron párok.

A kvark modell hazugság. Megbukik a Feynman-teszten, mivel nem illeszt be 7 nagyon fontos mezont. Végső soron léteznie kell egy olyan modellnek, amely sokkal egyszerűbb módon számolja be a fizikai jelenségeket.

79 E. J. Sternglass, Új bizonyítékok a mezon- és barionrezonancia állapotok molekuláris szerkezetére, Proceedings 2nd topical Conference on Resonant Particles, Ohio University, Athén, Ohio, június 10-12, [B.A. MUNIR] 55. o., 1965.

62. hazugság: A müonok elemi részecskék

A fizikában a 62. legnagyobb hazugság az, hogy a müonok elemi részecskék. A fizika standard modelljében a leptonoknak három szintje van, melyek három elektrontípust tartalmaznak: az elektron, a mu részecske vagy müon és a tau részecske vagy tauon. Mindegyiket elemi részecskeként kezelik, nem pedig összetett részecskeként.

Már az elején észrevettek egy matematikai összefüggést, amely jó bizonyíték volt arra, hogy a müon összetett részecske. Míg a három pion tömege nagyságrendileg közel van a finomszerkezeti állandó inverzéhez, ~137, addig a müon tömege 105,65 Mev/c 2 (millió elektronvolt osztva a fénysebesség négyzetével) ennek körülbelül a ¾ ezred része. Ez azt jelzi, hogy a négy részecske között egyszerű fizikai kapcsolat van. Még a Tauon tömege is majdnem pontosan 13 x 137 MeV/c 2 .

Ennek az egyszerű matematikai kapcsolatnak köszönhetően viszonylag könnyű olyan képleteket kidolgozni, amelyek az összetett részecskeszerkezetekhez vagy más típusú szerkezetekhez kapcsolódnak, és módosítani őket, hogy megközelítsék a pionok és a müonok ismert tömegét. Következésképpen számos tudós megtette ezt.

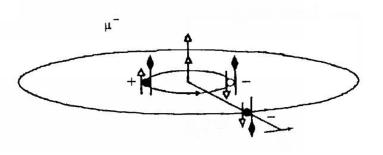
62-1. ábra Sternglass stílusú illusztráció egy müonról, amelynek közepén egy elektron-pozitron pár van, és egy elektron kering körülötte. A nyitott nyilak a szögimpulzust, a tömör nyilak pedig a mágneses momentumokat jelölik.

Ernest Sternglass több mint 50 évvel ezelőtt javasolta az egyik jobb modellt a müonhoz. A Sternglass-modell lényegében egy relativisztikus elektron-pozitron pár, amely körül egy elektron kering. 80 A Sternglass müon modell a 62-1. ábrán látható. Mivel a tér vákuumát virtuális elektron-pozitron párok töltik ki, a Sternglass modell a legegyszerűbb és legjobban illeszkedő a különféle javasolt müonmodellek közül.

Nyilvánvaló, hogy a müon egy rezonáns kompozit részecske, nem pedig elemi részecske a matematikai kapcsolata és a fizikai modellezés egyszerűsége miatt. A Sternglass modell továbbra is a legjobb kompozit modell a pionokhoz és a müonokhoz. Elmélete azt mutatja, hogy lehetséges az összes rezonanciát hasonló módon modellezni.

Vegyük észre, hogy Sternglass feljegyzéseiben megemlíti, hogy az 1960-as évektől származó dolgozataiban több hibát is elkövetett, ezért továbbra is szükség van arra, hogy valaki kézbe vegye a munkáját és kijavítsa a hibáit, miközben egyébként leegyszerűsíti, javítja modelljét, és leküzd bizonyos ellenvetéseket.

A fizikusok 50 éve hazudnak arról, hogy a müon elemi részecske. Valahogy a fizikusok ahelyett, hogy a müont összetett részecskeként kezelték volna, a müont elemi részecskeként jelölték meg.

80 Sternglass, E. J., „Electron-positron model for the charged mezons and pion resonances”, Il Nuovo Cimento, 1 Gennaio, Volume 35, Issue 1, pp. 227-260, 1965.

63. hazugság: Tauon elemi részecskék

A fizikában a 63. legnagyobb hazugság az, hogy a tauonok elemi részecskék. Amint az utolsó fejezetben említettük, a tauont tau-részecskének is nevezik, és ez a harmadik szintű elektron. A tauonról azt mondják, hogy a standard modell hatókörén belül elemi. Amint azt a 62. hazugságban tárgyaltuk, volt egy elég jó modell a müonra több mint 50 évvel ezelőtt, amit a fizikus közösség általában figyelmen kívül hagyott. Ez volt az Earnest Sternglass által javasolt modell a 62-1. ábrán.

63-1. ábra Sternglass stílusú illusztráció egy tauon modellről, amelynek közepén egy elektron van, amelyet egy elektron-pozitron pár keringtet.

A Sternglass-elmélet is használható a tauon ugyanolyan egyszerű kifejezésekkel történő magyarázatára. Történetesen létezik egy második orbitális megoldás is, amely egy virtuális elektron-pozitron párból és egy elektronból áll, a müon-modellből származó megoldáson kívül. Müon-modelljében az elektron az elektron-pozitron pár körül kering. Egy tauon modellezhető úgy, hogy a középpontban lévő elektron az elektron-pozitron pár körül kering.

Ebben az esetben az elektron-pozitron pár az elektron tömegközéppontja körül kering. Ez a második orbitális megoldás egy lényegesen magasabb energiájú állapot, amely megegyezik a tauon tömegenergiájával. A tömegenergia durva levezetése a dolgozatomban található egy tau részecskemodellben, amely a Sternglass elméleten alapul. 81

Mint minden Sternglass részecskemodellnél, ez is némi finomításra szorul; azonban azt mutatja, hogy a tau részecske, akárcsak a mü, nem elemi. Mivel a tauon tömegenergiája hozzávetőlegesen 13 x 137 MeV, számos módja lesz matematikai modellezésének, de a legegyszerűbb fizikai modell egy elektronból és egy elektron-pozitron párból áll majd. A tau-részecske szinte biztosan részecskék kombinációjának rezonáns állapota.

A fizikusok hazudnak, amikor azt mondják, hogy a tauonok elemi részecskék. Az elektron, müon és tauon közül csak az elektron elemi.

81 R. Fleming, „A tau részecskemodell a Sternglass elmélete alapján”,

https://www.researchgate.net/publication/283795752_Tau_Particle_Model_Based_on_the_Sternglass_Theory

64. hazugság: Az elektron-neutrínók elemiek

Ahogy e sorok írója, akit szíves figyelmedbe ajánlok, részletesebben is el fogja magyarázni azt, hogy az N- és Li-6 atommagok "rossz" statisztikái és a folytonos béta spektrum miatt kitaláltam egy kétségbeesett gyógymódot a statisztika "cseretételének" (1) és az energia-megmaradás törvényének megmentésére. Nevezetesen annak a lehetőségét, hogy az atommagokban létezhetnek elektromosan semleges részecskék, amelyeket neutronoknak nevezek, amelyek spinje 1/2, és engedelmeskedik a kizárási elvnek, és még abban különbözik a fénykvantumoktól, hogy nem haladnak a fény sebességével. A neutronok tömegének az elektron tömegével azonos nagyságrendűnek kell lennie, és semmi esetre sem lehet nagyobb 0,01 proton tömegnél. A folytonos béta-spektrum akkor lenne értelmes, ha feltételezzük, hogy a béta-bomlás során az elektronon kívül egy neutron is kibocsátódik úgy, hogy a neutron és az elektron energiáinak összege állandó. 82

Wolfgang Pauli, 1930

A fizika legnagyobb hazugságai közül a 64. az, hogy az elektron-neutrínók elemiek. Amikor a tudósok a radioaktív bomlást tanulmányozták, azt találták, hogy az sérti az energia-megmaradás elvét, ahogy azt akkoriban értelmezték. A kimutatható bomlástermékek különböző energiákkal rendelkeznek. Például amikor egy neutron lebomlik, felszabadul a keletkezéséhez szükséges ~780 keV, de az elektronok átlagos energiája kisebb, mint 400 keV. Pauliék elméjében a bomlásnak egyetlen rögzített maximális energiával kellett rendelkeznie (pl. 780 keV), így az energia valahogy elveszett, amikor egy alacsonyabb energiájú részecskét bocsátott ki. Nem volt kimutatható részecske, amely elviszi ezt az energiát, ezért szükségesnek találták, hogy kitaláljanak egyet.

A részecske feltalálásának alternatívája az volt, hogy elfogadjuk, hogy az energia-megmaradás elve nem minden helyzetben igaz. Mivel a fizikusok nem voltak tisztában a béta-bomlás magyarázatára szolgáló fizikai mechanizmussal, és nem voltak készek lemondani az energia-megmaradás elvéről, egy új részecske feltalálása látszott a járható útnak. Azok számára, akik nem ismerik, vegyék figyelembe, hogy a béta-részecskék ugyanazok, mint az elektronok, és a béta-bomlás magában foglalja az elektronokat és a pozitronokat egyaránt érintő bomlási kölcsönhatásokat.

Ennek a kitalált részecskének elektromosan semlegesnek, nagyon kicsinek, kis tömegűnek vagy egyáltalán nem kellett volna rendelkeznie tömeggel, különben közvetlenül láthatnánk. Wolfgang Pauli volt az első, aki felvetette egy ilyen részecske létezését, amelyet a fejezet elején idézett levélben neutronoknak nevezett. Enrico Fermi továbbfejlesztette Pauli koncepcióját, és kitalálta a neutrínó nevet. 83

Idővel, amikor felfedezték a gerjesztett elektronállapotokat, amelyeket mü és tau elektronoknak neveznek, úgy gondolták, hogy mü és tau neutrínóknak is kell lenniük, és így megvan a standard részecskemodell három neutrínója. Ezenkívül vannak antineutrínók, így a lepton konzerválása megőrizhető, mivel az antilepton kiiktatja a leptont ebben a szabályalapú képletben. Mivel ezen elmélet szerint a neutrínók folyamatosan sugároznak ki, úgy gondolják, hogy az univerzumban van egy neutrínó-mező, amely rengeteg szinte kimutathatatlan energiát, sőt talán tömegenergiát is tartalmaz.

A neutrínóelmélet azonban nem ad fizikai modellt a béta-bomlás tényleges végbemenetelére, és nem magyarázza meg, hogyan létezik az energiaeloszlás, és hogyan történik ez az eloszlás fizikailag. A jelenlegi elmélet szerint az energiaeloszlás valahogy varázslatosan megtörténik, és a neutrínó felveszi ezt a kifolyó fölösleget.

A béta-bomlás és annak energiaeloszlása tényleges magyarázatához ennek az új részecskének, vagy bármi hasonlónak, a kölcsönhatás elején kell lennie, és energiával kell hozzájárulnia a kölcsönhatáshoz. Ekkor a kibocsátott részecske, jellemzően egy elektron vagy pozitron, rendelkezik a maradék energiával. A neutrínók az egyenlet rossz oldalán állnak, mivel azok a béta-bomlás és annak energiaeloszlásának tényleges fizikai okai. A standard modell fizikusai hazudnak, mikor azt mondják, hogy megértik a béta-bomlás valódi okát.

A standard modellt fizikusai szeretnek úgy tenni, mintha a gyenge interakciós elmélettel kezelték volna ezt az alapvető problémát, de nem. Hazudnak, ha azt mondják, hogy ismerik az energiaeloszlás okát, és hazudnak, ha azt mondják, hogy egy neutrínó felelős az energiaeloszlásért.

Tehát mi okozza valójában a béta-bomlást és az energiaeloszlást? Amire szükségünk van, az nem áll messze attól, amit Pauli javasolt. Szükségünk van egy csomó „kis semleges dologra”, amelyek energiáinak széles skálája van. Ezeknek a „kis semleges dolgoknak” a valószínűségi keresztmetszetnek megfelelően kölcsönhatásba kell lépniük a bomlásnak kitett magokkal. Ezeknek a „kis semleges dolgoknak” mindig jelen kell lenniük az univerzumban. Egy mezőt kell alkotniuk az egész térben.

Ez a mező nem neutrínó, mivel nincs mechanizmus az egyes szabad neutrínók előállítására az űrben. A neutrínóknak nincs nyilvánvaló fizikai mechanizmusa, mondjuk, hogy megragadják a neutron elektronszerű részét, és felszabadítják az elektront.

Szerencsére van egy mező, amely megfelel a követelményeinknek, a nullapontos mező, és vannak olyan dipólusai, amelyek megfelelnek a „kis semleges dolgok” követelményének. A vákuum-ingadozások összességében véve elektromosan semlegesek; nincs tömegük, és közvetlenül nem észlelhetők. Nekik is van energia-folytonosságuk.

Létezik egy nyilvánvaló kölcsönhatási mechanizmus is, amely nagyon hasonlít az 57. és 58. fejezetben bemutatott kvantumugrások mögötti mechanizmushoz. A szabad elektron egy virtuális pozitronnal megsemmisül, és az egyszeri virtuális elektron szabaddá válik. Bővítésképpen a neutron elektronszerű része egy pozitronnal megsemmisül, protonná alakítva a neutront, és szabadon hagyva az egykor virtuális elektront. Ily módon az elektron-proton ~780 keV potenciálgáton átugrik, és a protonnal együtt kiszabadul a bezártságából.

Ez a folyamat könnyen megfordítható, így az elektron át tud ugrani a protont körülvevő potenciálgáton, és neutront hoz létre. Ebben az esetben a virtuális elektron-pozitron párral való kölcsönhatás úgy tűnik, hogy az elektron áthaladt a potenciálgáton. Ez a virtuális párok által közvetített megsemmisülési-megjelenési események egy szélesebb osztályának sajátos esete, amit kvantumalagútnak neveznek.

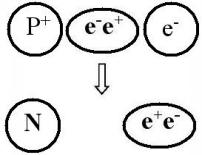
64-1 ábra Egy neutron elektron-pozitron megsemmisülési-megjelenési kölcsönhatás révén jön létre.

A vákuum-fluktuációs részecskepárokat, az elektron-pozitront, valamint a proton-antiprotont magában foglaló annihilációs-megjelenési kölcsönhatások felelősek az összes béta-bomlási kölcsönhatásért. További részletekért olvassa el néhány dolgozatomat. 84,85,86

Érdekes módon a hiányzó energia a nullapont mezőből származik. Neutrontermelés esetén a nullponti energia beépül a neutronba, majd ha egy neutron lebomlik, az energia visszakerül a nullponti mezőbe. De mivel a neutron energiája kezdetben eltolt vákuumenergia, nincs az energiamegmaradás megsértése. A nullponti energia az energia. A megsemmisülési-megjelenési események lehetővé teszik, hogy a nullponti energia egyensúlyba hozza a lendületet, épp úgy, mint az atomi pályákon.

Louis De Broglie feltételezte, hogy a fotonok neutrínókból állnak, és mindegyik fél hullámhosszon van egy-egy új neutrínó. Mivel egy foton fél hullámhosszú virtuális elektron-pozitron párból áll, Broglie feltételezése helyett arra a következtetésre juthatunk, hogy a neutrínó úgy néz ki, mint egy virtuális elektron-pozitron pár. Ez visszavisz teljes egészében minket a virtuális elektron-pozitron párok által közvetített gyenge kölcsönhatásokhoz.

De feltehetjük a kérdést, mi a helyzet a neutrínóészlelési kísérletekkel? Mit észlelnek? A válasz az, hogy többnyire a nullpont-mezőt észlelik. Végtére is nem kell nullpont-mezőnek és neutrínómezőnek egyszerre lennie, amikor a nullapont-mező önmagában magyarázhatja az összes fizikai jelenséget.

Mint említettük, van egy hipotetikus modell a neutrínókra, amely lehetővé teszi számukra, hogy lineáris és szögimpulzusokat hordozzanak, miközben egyúttal a nullapont mező részei is.

A De Broglie-hipotézisben van egy csavar, a neutrínó, ami, akárcsak a foton, forgó virtuális-elektron-pozitron párok sorozatából áll, de ellentétes forgás helyett ugyanabba az irányba forognak. Ez az összetett neutrínó modell lehetővé teszi a neutrínók kibocsátását és észlelését. És ebben a modellben az antineutrínók ugyanazok, mint a neutrínók.

Mindenesetre hazugság azt állítani, hogy az elektronneutrínók elemiek. Az elektronneutrínók nem mások, mint vákuumfluktuációs dipólusok, vagy esetleg vákuum-ingadozási dipólusok kombinációi, és a vákuum-ingadozások azok, amelyek elemiek.

82 W. Pauli, „Nyílt levél a radioaktív emberek csoportjához a tübingeni Gauverein-találkozón”, 1930. december 4. (Fordítás: Kurt Riesselmann)

83 E. Fermi, Z. Physik 88 161, 1934. 84 R. Fleming, „A béta-bomlás, mint a Hawking-sugárzással analóg virtuális részecske-kölcsönhatás”

http://vixra.org/pdf/1204.0050v1.pdf

85 R. Fleming: „A neutrínók mint vákuum-ingadozási részecskepárok”

http://vixra.org/pdf/1503.0027v1.pdf

86 R. Fleming „A kvantumugrások, mint a Hawking-sugárzással analóg vákuum-fluktuációs részecskepár kölcsönhatások”

http://gsjournal.net/ScienceJournals/Research%20PapersQuantum%20Theory%20/%20Particle%20Physics/Download/6179

65. hazugság: A Mu és Tau neutrínók elemiek

A fizikában a 65. legnagyobb hazugság, hogy a mü, a tau neutrínók elemiek. Mivel a 64. hazugság, hogy az elektronneutrínók elemiek, nyilvánvaló következménye, hogy a mü és tau neutrínók eleminek nevezése is hazugság. Vannak azonban lényeges különbségek is. Ahogy az utolsó fejezetben említettük, a neutrínókról úgy gondolják, hogy három formában léteznek, amelyek megfelelnek annak az elektronnak, amellyel kölcsönhatásba lépnek. A három elektrontípus az elektron, a mü elektron vagy müon és a tau elektron vagy tauon. Következésképpen úgy gondolják, hogy létezik egy elektronneutrínó, egy mü-neutrínó és egy tau-neutrínó, amelyek kölcsönhatásba lépnek a megfelelő elektrontípusukkal.

Mindegyik neutrínótípushoz tartozik egy kiegészítő antineutrínó; azonban az antineutrínó ugyanaz lehet, mint egy neutrínó. Ez hasonló lehet ahhoz, ahogy az antifoton ugyanaz, mint a foton. Ebből a szempontból, és amint azt az utolsó fejezet is javasolta, a fotonok és a neutrínók közötti hasonlóságok sokkal nagyobbak, mint a standard modellben javasolták.

A müonneutrínókat 1962-ben fedezte fel egy kutatócsoport, akik 1988-ban Nobel-díjat nyertek felfedezésükért. 87 Azt fedezték fel, hogy amikor a pionbomlás során kibocsátott neutrínók kölcsönhatásba léptek az anyaggal, inkább müonokat, sem mint elektronokat termeltek. Egy normál elektronneutrínótól elvárható, hogy elektront termeljen, amikor kölcsönhatásba lép az anyaggal. Vegye figyelembe, hogy a müon ezután úgyis elektronná bomlik.

Az előző fejezetből és a kapcsolódó írásokból jól látható, hogy a virtuális elektron-pozitron párok hogyan töltik be a neutrínók szerepét a béta-bomlási folyamatok modellezésében. A szabályos elektronneutrínónak nem kell egy másik részecske bomlásából származnia, hiszen az éterben bármely virtuális elektron-pozitron pár lehet, amelyik a megfelelő energiatartományba esik.

Ami nem azonnal világos, az az, hogy a bomló pion miként vezet müontermeléshez és csak müontermeléshez. Könnyebben belátható, hogy mi történik, ha megnézzük az alábbi ábrákon látható Sternglass modelleket a pionhoz és a müonhoz.

65-1. ábra Sternglass stílusú illusztrációk egy pionról (fent) és egy müonról (lent). A nyitott nyilak a szögmomentumot, a zárt nyilak pedig a mágneses momentumot jelzik.

Természetesen az első dolog, ami beugrik, az az, hogy mindkét részecskében van egy gyorsan forgó elektron-pozitron pár. Ez azt jelenti, hogy a pionbomlással kapcsolatban egy pionszerű elektron-pozitron pár jön létre, és müont alkot.

Ez a szögimpulzus megőrzésének problémájának tűnik.

Azt is figyelembe kell vennünk, hogy mivé bomlik le egy pion, ami két foton, egy elektron és egy pozitron, egy foton plusz egy elektron-pozitron pár vagy két elektron-pozitron pár. A töltött pionok müonná bomlanak, közbenső lépésként, hogy végül elektronokká bomoljanak le. A Sternglass-modellben a töltött pion lényegében egy gerjesztett müon. A standard modellben a bomlási folyamat minden lépése után neutrínók vagy antineutrínók lesznek kibocsátva ki.

A kérdés az, hogy mi történik a pion szögimpulzusával? Ezt a szögimpulzust meg kell őrizni. A fotonok vagy az egyes elektronok vagy pozitronok nem tudják elvinni. A szabad elektron-pozitron párok sokkal kisebb szögimpulzusokat hordozhatnak, mint a pozitrónium. Úgy tűnik, hogy a közvetlenül kimutatható bomlástermékek egyike sem jelent megoldást.

Az egyetlen lehetőség az, hogy a pion szögimpulzusát a mü-neutrínónak kell elvinnie, bármi legyen is az. De ahhoz, hogy ekkora lendületet hordozzon, magának a mü-neutrínónak relativisztikusan forgó virtuális elektron-pozitron párok sorozatából kell állnia. A végén hasonlóan, mint egy foton, de ahelyett, hogy minden egymást követő pár ellentétes irányba forogna, ugyanabba az irányba kell forognia, megőrizve ezzel a szögimpulzust. Ez összhangban van az előző fejezetben említett hipotetikus modellel.

A tau részecske nagyobb tömegenergiája miatt még nagyobb szögimpulzussal rendelkezik, mint a mü részecske. Következésképpen a tau neutrínónak nagyobb szögimpulzussal is kell rendelkeznie, bár a mü és tau neutrínó egyébként ugyanaz.

Ez a nagy mennyiségű szögimpulzus arra is ad okot, hogy a mü és tau neutrínók miért nem lépnek túl gyakran kölcsönhatásba a közönséges anyagokkal, mivel általában nincs mód arra, hogy a szögimpulzust a legtöbb részecske, atom vagy molekula által elnyelje.

A virtuális elektron-pozitron párok az elektronneutrínók képében nem lépnek kölcsönhatásba a közönséges stabil anyaggal. Kölcsönhatásba lépnek olyan atomokkal, amelyek béta-bomlási folyamatoknak vannak kitéve. Vegye figyelembe, hogy mivel a vákuum-ingadozások mindenhol jelen vannak, gyakran fogunk látni úgynevezett elektronneutrínókat, miközben mü vagy tau neutrínókat várunk.

Kiegészítő megjegyzésként a neutrínók hipotetikusan más valós virtuális részecskepárokból is állhatnak, ha ezek a párok egy kölcsönhatás részét képezik, bár az összes rezonancia bomlástermékei alapján úgy tűnik, hogy elektron-pozitron párokkal készülnek.

Az elektronneutrínóhoz hasonlóan hazugság, ha azt állítjuk, hogy a mu-neutrínók és a tau-neutrínók elemiek. Minden neutrínó egy vagy több virtuális részecskepárból álló összetett részecskének tekinthető.

87 G. Danby, J. M. Gaillard, K. Goulianos; L. M. Lederman; N. B. Mistry; M. Schwartz; J. Steinberger, "A nagyenergiájú neutrínó reakcióinak megfigyelése és kétféle neutrínó létezése". Fizikai áttekintő levelek. 9:36, 1962.

66. hazugság A neutrínóknak tömegük van

A fizika legnagyobb hazugságai közül a 66. a neutrínók tömege. A fizikusok elkeseredettségében, hogy megmentsék Newton és Einstein kudarcra ítélt gravitációs elméleteit, belevágtak a fegyverbe, és eldöntötték, hogy a neutrínóknak van tömegük, mivel a neutrínó tömege lehet a hiányzó sötét anyag. Amint azt az előző hazugságokban tárgyaltuk, a gravitációs elméletek elavultak, és nincs ok arra, hogy sötét anyagot vagy hiányzó tömeget keressünk, mert ezekből a modellekből mindvégig hiányzott egy vagy több erő.

A fizikusok úgy döntöttek, hogy a neutrínóknak azért van tömegük, mert a három típus között oszcillálnak, így egy mü-neutrínó később elektron-neutrínóként jelenhet meg. Ezek összekapcsolásának módja nincs fizikailag logikusan megmagyarázva, mivel nem fizikai magyarázaton alapulnak. A neutrínó tömegét alacsonynak mondják, de nincs mechanizmus arra, hogy egy neutrínó hogyan tudja kiváltani a nagyon hosszú hullámhosszú, alacsony energiájú vákuum-ingadozásokat.

Ha figyelembe vesszük a béta-bomlást, amely leginkább vákuum-fluktuációs kölcsönhatásként magyarázható, ezeknek a „neutrínóknak” biztosan nincs tömege. Ezek vákuum-ingadozások, és a vákuum-ingadozásoknak önmagukban nincs tömegük. A vákuum-ingadozások sorozatából álló neutrínónak sincs tömege. A fotonoknak nincs tömegük, és a fotonokhoz hasonló neutrínóknak, kivéve szögimpulzusukat, szintén nincs tömegük.

Az ilyen típusú neutrínók tömege nem egyenlő az energiájával, ahogy a foton tömege sem a foton energiájával. A megfigyelt oszcillációkat leginkább a fotonszerű neutrínók közötti szögimpulzus-transzferrel magyarázhatjuk.

Az az elképzelés, hogy a neutrínóknak tömegük van, hazugság. Az egész térben nincs neutrínó-mező, amely a hiányzó tömeget kiadná, ami valójában nem is hiányzik.

67. hazugság: A W & Z bozonok gyenge kölcsönhatást közvetítenek

A fizika legnagyobb hazugságai közül a 67. a W és Z bozonok gyenge kölcsönhatásokat közvetítenek. Annak a hipotézisnek, hogy a W és Z bozonok gyenge kölcsönhatásokat közvetítenek, számos hibája van. Ez a hipotézis annyira rossz, hogy valóban elgondolkodtat a benne hívők intellektuális képességein. Ahogy a 18. hazugságban láttuk, az erőkölcsönhatások mérőbozonmodelljével kapcsolatos problémáknak hosszú listája van. A W és Z bozonmodell még több problémát okoz.

A W-vel és Z-vel kapcsolatos további problémák közül sok a 80 GeV-os (giga-elektron-volt) tömegenergiához kapcsolódik a W-hez és a 91 GeV-hoz a Z esetében. Mindkettő több mint 85-ször nagyobb tömegű, mint egy proton. De végül az elmélet kudarcot vall, mert van egy sokkal egyszerűbb elmélet, amelyet a 64. fejezetben röviden ismertetünk, és amely elmagyarázza, mi történik egy egyszerű fizikai modellben, és a W/Z elmélet számos hibája nélkül.

A tömeg nélküli fotonok elég rossz variáció, épp úgy, mint a mérőbozonok, de ha tömeg nélküli bozonunk is van, a dolgok sokkal rosszabbak lesznek. Nem lehet stabil vagy metastabil W vagy Z részecskét előállítani egy sokkal kisebb tömegű protonból vagy elektronból anélkül, hogy megsértené az energia-megmaradás elvét. A kivétel az lenne, ha olyan rövid életű lenne, hogy egy anyag-antianyag részecskepárként létező vákuum fluktuációról lenne szó, amely nem haladja meg a Planck-energiát.

A következő probléma, amely mind a tömeg-, mind az energia-megtakarítással kapcsolatos, az úthossz.

Azok, akik a hipotetikus W/Z elméletet támogatják, azt mondják, hogy a korlátozott úthossz az elmélet része, amely megfelel a gyenge interakciós megfigyeléseknek. A probléma az, hogy a W és Z részecskék megengedett úthossza az energia-megmaradás elvének megsértése nélkül túl rövid. Ez komoly probléma, nem pozitív tulajdonság.

Ezek a feltételezett mérőbozonok nem létezhetnek elég sokáig ahhoz, hogy kikerüljenek egy protonból vagy neutronból, mivel nem létezhetnek 1,3 x 10-26 másodpercnél tovább anélkül, hogy megsértenék az energia-megmaradás elvét. Ezalatt egy W-részecske legfeljebb 3,9 x 10-18 métert tud megtenni, a Z pedig ennél is kevesebbet. Összehasonlításképpen a proton sugara 0,8775 x 10 -15 méter, és a neutron sugara is hasonló. Ahhoz, hogy a neutron protonná és elektronná bomoljon, az elektronnak ki kell jutnia a proton ~780 keV potenciálgátján, ami sokkal nagyobb, mint a proton sugara. A W/Z modell nem működik.

Ezenkívül a W/Z hipotézis megsérti a részecskék felezési idejére vonatkozó kísérleti méréseket, mivel ez is korlátozza az utazási távolságukat. A 3 x 10 -25 másodperces felezési idő alatt egy W csak 9 x 10 -17 métert tud megtenni, ha fénysebességgel mozog, ami körülbelül egytizede a proton sugarának. Egy W-részecskének meg kell sértenie az energia-megmaradás elvét és/vagy a fénysebesség határát ahhoz, hogy az elektron kiszabaduljon a protonból.

Még ha a W vagy Z virtuális anyag-antianyag részecskepárként létezne is, az elektron létrehozása a bomlás részeként ismét sértené az energia-megmaradás elvét. Az elmélet azonban még csak nem is foglalkozik a részecskepár lehetőséggel, így sérti az energia-megmaradást, akárhogyan is nézzük.

Szerencsére létezik egy sokkal egyszerűbb mechanizmus a gyenge kölcsönhatások magyarázatára. A virtuális részecskepárok által közvetített megsemmisülési-keletkező kölcsönhatások felelősek az összes béta-bomlási kölcsönhatásért. A W és Z egyszerűen nem szükséges a gyenge kölcsönhatások magyarázatához.

Az az elképzelés, hogy a W és Z bozonok gyenge kölcsönhatásokat közvetítenek, hazugság. Ez a modell semmilyen módon nem felel meg az energiatakarékosság elvének, és nem is szükséges, hogy megfeleljen.

68. hazugság: W & Z részecskék

A fizika legnagyobb hazugságai közül a 68. a W és Z részecskék. Az előző hazugság alapján kristálytisztán világosnak kell lennie, hogy a W és Z részecskék nem közvetítenek gyenge kölcsönhatást, így nem meglepő, hogy a W és Z részecskék valódi természetét meg kell kérdőjelezni.

Vákuumfluktuációs részecskepárok, elsősorban virtuális elektron-pozitron párok közvetítenek minden gyenge kölcsönhatást. Még ha a W és Z kölcsönhatás elméletét hinnénk is, az sérti az energia megmaradás elvét. Az intelligens részecskemérő bozonelmélet szintén hazugság, amint azt a 18. hazugság tárgyalja, még e további nehézségek nélkül is.

Fogadok, hogy néhányan azt gondolják, „de vannak kísérleti bizonyítékok a W és Z részecskékre”. Bebizonyosodott, hogy léteznek." A tárgyi bizonyítékok azonban egyáltalán nem erre utalnak. A kísérletek rövid életű rezonanciákat mutattak ki ~3 x 10-25 másodperces felezési idővel. Nincs közvetlen fizikai bizonyíték arra vonatkozóan, hogy mik ezek a rezonanciák, vagy mit csinálnak.

A W-t és a Z-t nem is közvetlenül észlelik, hanem a bomlástermékeik alapján azonosítják. Még részecskének nevezni is tudománytalan. Alig teljesítik a rezonancia statisztikailag szignifikáns mérésére vonatkozó követelményeket.

Nincs közvetlen fizikai bizonyíték arra, hogy ezek a rezonanciák részt vesznek azokban a reakciókban, amelyekben állítólag közreműködnek. A tudósok egyszerűen úgy döntöttek, hogy ezeket a rezonanciákat egy létező elmélettel párosítják, egyszerűen azért, mert el akarták hinni, hogy ez igaz, hogy Nobel-díjat kapjanak érte. Azt mondani tehát, hogy ezek a rezonanciák gyenge kölcsönhatásokban vesznek részt, tudománytalan dogma.

Jelenleg nincs jó fizikai modell ezekre a nagy energiájú rezonanciákra, de megnézhetjük bomlástermékeiket, hogy megjósolhassuk a felépítésüket. Mindkét W azonos töltésű elektronná, müonná vagy tauonná bomlik, az azonos típusú neutrínóval együtt. A tauon és a müon közvetlenül elektronná bomlik, így egy elektron vagy pozitron, plusz rengeteg energia fotonok és neutrínók formájában marad vissza, amikor egy W lebomlik.

A Z-bozon részecskepárra bomlik, így vagy egy elektron-pozitron párt, egy müon és anti-müon párt, vagy egy tauon és anti-tauon párt látunk. Végül a müon és tauon pár elektron-pozitron párrá bomlik, plusz fotonok és neutrínók.

Következésképpen a W részecskék Sternglass típusú modelljében egy elektron vagy pozitron van egy vagy több rezonáns részecskepárral együtt. A Z-bozonnak van egy elektron-pozitron párja, valamint egy vagy több további rezonáns részecskepár. Mindkét esetben a részecskepárok lehetnek elektron-pozitron párok, vagy lehetnek más típusú valós virtuális részecskepárok.

Végső soron a W és Z összetett részecske-összetétele egy rejtvény, amely arra vár, hogy valaki megfejtse, aki hajlandó ezért erőfeszítéseket tenni. Több mint valószínű, hogy amikor valaki erre rájön, a Sternglass részecskeelméletnek megfelelő módon fogja modellezni.

A W és Z részecskék léte hazugság. A W és Z részecskék nem elemi részecskék. Nem mások, mint két vagy több részecske kombinációjának rezonáns állapota.

69. hazugság: Az erős nukleáris kölcsönhatás a Gluonoknak köszönhető

A fizikában a 69. legnagyobb hazugság a gluonok miatti erős kölcsönhatás, a magerő. Az erős nukleáris erő az az erő, amely a protonokat és a neutronokat egy atommagban köti össze. Az erős nukleáris erő nélkül a protonok közötti elektrosztatikus taszítás az atommagok szétválását okozná, ha egynél több proton van az atommagban.

A nukleáris erőnek elég erősnek kell lennie ahhoz, hogy a protonokat egymás közelében tartsa, még akkor is, ha pozitív elektromos töltésük miatt taszítják őket. Ez az erő akár 100-szor erősebb, mint a Coulomb taszítás, de ha túl közel érnek, 0,7 x 10 -15 méteres nagyságrenden, létrejön egy taszító erő. Ennek ellenére két proton nem fog vonzódni egymáshoz anélkül, hogy legalább egy neutron lenne az atommagban. A legtöbb stabil atommagban legalább annyi neutron van, mint proton.

A kvarkelmélet szerint a gluonok, mint a szorosan összefüggő erős kölcsönhatás részei, összetartják a kvarkokat, és részecskéket, legfőképpen protonokat és neutronokat képeznek. Ennek a gluon által közvetített erőnek a fennmaradó része feltehetően felelős a protonokat és neutronokat az atommagban együtt tartó nukleáris erőkért.

A kvarkelmélet előtt a mezonok az erős kölcsönhatás-elmélet mérőbozonjai voltak. De most a fizika standard modellje szerint, a gluonokról azt mondják, hogy az erős kölcsönhatás mérőbozonjai. Akár a gluon-modellről, akár az erős erők mezonmodelljéről beszélünk, a mérőbozonok általában hazugságok a 18. hazugságban tárgyalt okok miatt. Tehát, ha valaki átmegy„old-school”-ba, és azt mondja, hogy a mezonok közvetítik az erős kölcsönhatást, akkor is hazudik.

Ennél is fontosabb, hogy van egy sokkal elegánsabb alternatív magyarázat az erős kölcsönhatásra, egy olyan magyarázat, amely egyesíti az erős kölcsönhatást az elektromágneses elmélettel. Ez egy olyan erő, amely mindig az egymáshoz közeli tárgyak között létezik, a Casimir-erő.

Míg az eredeti Casimir-elmélet két lemez közötti hatást jósolta meg, az első meggyőző kísérleti megerősítés megerősítette, hogy a gömb és a lemez között egy erő létezik.A Casimir-effektus két gömb között is fellép, a szórási kísérletek során a protonokat gömb- vagy kvázi gömbalakú objektumoknak találták. A neutronok gömb alakúak is, nagyjából azonos méretűek. Ennek alapján a protonok között, a neutronok neutronok között, valamint a protonok és neutronok között Casimir-erőknek kell lenniük.

Kiderül, hogy ha kiszámítja a Casimir-erőt két protonnyi gömb között, akkor az elég erős ahhoz, hogy megfeleljen az erőskölcsönhatás nagyságának, miközben az elektrosztatikus taszítást is legyőzi. Egy egyszerű számítás, amely a magerőkre vonatkozik, azt mutatja, hogy a vonzó Casimir-erő két gömb között legalább 17-szerese az elektrosztatikus taszításnak. További információkért olvassa el a Nuclear Force Computed as the Casimir Effect Between Spheres 88 című írásomat.

Vegye figyelembe, hogy a cikk a teljes Casimir-erőnek csak egy komponensét írja le, mivel csak a protonok közötti legközelebbi határokon lévő nyomáskülönbségeket tartalmazza. A tanulmány nem veszi figyelembe, hogy a gömb alakú részecskék maguk is Casimir-üregek, és a részecskék külső felületéről további nyomás jön létre. Ha a Casimir-erőhöz való összes hozzájárulást figyelembe vesszük, az erők összesen körülbelül 100-szor nagyobbak, mint a Coulomb-taszítás.

Azt mondják, hogy a részecskék egymáshoz közeledésekor fellépő taszító erő az erős kölcsönhatás része, de a két ellentétes irányú erőt a legjobban két különálló erőként kezelni. Egyes fizikusok azt állítják, hogy a taszító erő Pauli kizárási elvének köszönhető. Pauli kizárási elve azonban nem alapvető erő, mivel nem magyarázza meg a protonok és neutronok közötti taszító erőt. A nukleonok közötti taszító erő Pauli-féle kizárási elvének magyarázata egy újabb hazugság.

Amit ebben a könyvben eddig azonosítottunk taszító erőket az elektronok, protonok és neutronok, valamint a protonok és elektronok, valamint a neutronok és protonok között fordult elő. Ezek együttesen teljesen más erők, mint az erős kölcsönhatás. Egy másik hazugság azt állítani, hogy a protonok közötti taszító erő az erős kölcsönhatás része.

Tehát most ismét módosítanunk kell az alapvető erők listáját. Azaz:

1. mechanikai erő,

2. elektromágneses erő,

3. gyenge erő,

4. erős erő,

5. sötét erő,

6. nagy energiájú gravitációs erő,

7. taszító erő az elektronok és a protonok között,

8. taszító erő az elektronok között,

9. taszító erő a protonok között,

10. taszító erő a protonok és a neutronok között,

11. taszító erő a neutronok között.

Az az elképzelés tehát, hogy az erős kölcsönhatás a gluonoknak köszönhető, hazugság, csakúgy, mint az a régebbi elképzelés, amely szerint a mezonoknak köszönhető. Az erős kölcsönhatás Casimir-erő, és ugyanilyen fontos, hogy a magerők nem különálló erők, hanem az elektromágneses erő részét képezik.

88 R. Fleming, „The Nuclear Force Computed as the Casimir Effect Between Spheres”,

https://www.researchgate.net/publication/283795494_The_Nuclear_Force_Computed_as_the_Casimir_Effect_Between_Spheres

70. hazugság: Gluonok

A fizika legnagyobb hazugságai közül a 70. a gluonok. Miután a fizikusok meggyőzték magukat arról, hogy a fotonok csererészecskék vagy mérőbozonok, amelyek az elektromágneses erőket hordozzák, annyira megtetszett nekik az ötlet, hogy új méretű bozonokat találtak ki az összes ismert erő számára. Yukawa eredetileg azzal a Nobel-díjat nyerő ötlettel állt elő, hogy a mezonok, pontosabban az újonnan felfedezett pionok az erős kölcsönhatás mérőbozonjai. 89

Miután a kvarkelmélet érvényesült, a fizikusok szükségét érezték egy új mérőbozon feltalálásának, amely erőcsere-részecskeként működik a kvarkok között. Sajnos soha nem gondoltak túl kritikusan a részecskecsere-hipotézis mögött meghúzódó logikára vagy annak hiányára. Ha szükséges, tekintse át a 18. hazugságot.

Nos, mivel könnyen kimutatható, hogy a Casimir-erő magyarázza meg az erős kölcsönhatást, nincs szükség arra, hogy a magerőhöz mérőbozon társuljon. A Carimir-erő a vákuum fluktuációs dipólusok közötti van der Waals erőknek köszönhető, amelyekről ismert, hogy minden más hipotézistől függetlenül léteznek.

Érdekes módon a virtuális elektron-pozitron és proton-antiproton párok hatására a neutronok protonokká, a protonok pedig neutronokká alakulnak az atommagban. Az elektronok és protonok cseréje ugyanúgy közvetített, mint a neutronképződésnél és -bomlásnál, de a magon belüli szoros távolság miatt mindkét lépés meglehetősen azonnal megtörténik.

A gluonok léte hazugság. Az a régebbi elképzelés, hogy a mezonok mérőbozonok lennének, szintén hazugság. Nincs szükség erőcsere részecskékre az erős kölcsönhatás magyarázatához.

89 H. Yukawa, "On the Interaction of Elementary Particles", PTP, 17, 48, 1935.

71. hazugság: Az elektronokra nem hat az erős kölcsönhatás

A fizikában a 71. legnagyobb hazugság az, hogy az elektronokra nem hat az erős kölcsönhatás. Megjegyzendő, hogy ez nem azt jelenti, hogy az elektronok az erős nukleáris erő hatására kölcsönhatásba lépnek a protonokkal és a neutronokkal, mert a későbbiekben világossá váló okokból nem. Nem, a lényeg az, hogy van egy ekvivalens magerő, amely vonzza az elektronokat egymáshoz. Erős bizonyíték van erre az elektronmegkötő erőre, de valamiért mégsem szerepel a mainstream fizika standard modelljében.

Mi a bizonyíték, amit elfogadsz ezzel kapcsolatban? Tekintsük a villámlást példaként. A villám szabad szemmel úgy néz ki, mint egy fénycsík az égen. A valóságban ezek a csíkok elektronokból állnak, és ezek az elektronok egy csomagban utaznak. Ahogy az elektrosztatikus töltés felhalmozódik, egy elektroncsoport összegyűlik akár felhőben, akár a Földön, és amikor az elektromos potenciálkülönbség, a feszültségkülönbség elég nagy, ív keletkezik, és ezekből az elektronokból álló csomag átugrik a potenciálrésen.

Ne feledje, hogy ez bármikor megtörténik, amikor ív keletkezik, még akkor is, ha megrázza magát a valamihez súrlódó statikus elektromosság felhalmozódása miatt. Az elektroncsomag olyan gyorsan mozog, hogy szemünk pont vagy golyó helyett vonalat lát, kivéve a ritka lassan mozgó jelenségeket, például a gömbvillámot.

A kérdés tehát az, hogy hogyan jön létre ez a csomag? Ha csak az erőket vesszük figyelembe a standard modellben, akkor egy negatív töltésű elektronokkal teli csomagot kapnánk, ahol minden elektron taszít minden más elektront. Ha a standard modell leírná az összes erőt, azok az elektroncsomagok felrobbannának. Nem lenne sem elektroncsomag, sem ívek, sem villámlás.

Ahhoz, hogy mindennapi megfigyeléseink igazak legyenek, szükség van egy további erőre, amely az elektronokat egymáshoz vonzza. Míg néhány kutató megvizsgálta ezt a problémát, jelenleg nincs széles körben elfogadott elmélet a magyarázatra. Érdekes módon ugyanaz az erő működik, mint a 69. hazugságban bemutatott erős kölcsönhatás-elmélet.

Az elektronok közötti elektrosztatikus taszító erőt legyőző erő a Casimir-erő. Ha az elektronok elég közel vannak egymáshoz, akkor a Casimir-erő összefűzi őket, legyőzve az elektrosztatikus taszítást, ugyanúgy, ahogy a protonok kötődnek egymáshoz. Az ok, amiért az elektronokat és a protonokat nem nyomja össze a Casimir-erő az az, hogy nagymértékben különböznek egymástól, nem azért, mert az erős Casimir-erő valahogy nem hat az elektronokra.

Megjegyzendő, hogy ez az elmélet azon alapul, hogy az elektronok sugara megegyezik az elektron tömegével a nullponti energia elmozdulása miatt, ami 1,6 x 10-12 méter nagyságrendű. Összehasonlításképpen a proton sugarát 0,88 x 10-15 méterben mérték. Az elektronok közötti erős Kázmér-erőről további információkért olvassa el a Casimir Attraction Between Electrons című írásomat. 90

Kiderül, hogy az erős Casimir-erőn kívül más erőnek is kell lennie. Ha csak az erős Casimir-erő létezne, és az elektronszerkezet az átmérőjénél jóval kisebb vákuum-ingadozásokkal lép kölcsönhatásba, akkor az erős Kázmér-erő olyan erőssé válna, hogy az elektronok soha nem válnának szét. Tehát, amint azt a protonoknál láttuk, az elektronok között nagyon közeli tartományban taszító erőnek kell lennie. Korábban ugyanerre a következtetésre jutottunk, amikor az atomi pályán lévő elektronokat vizsgáltuk.

Talán az is felmerül benned, hogy mivel az elektronok egyfajta erős erő hatására lépnek kölcsönhatásba, miért nem alkotnak az atommagokhoz hasonló stabil csoportosulásokat. A válasz erre egyszerű; nincs elektromosan semleges részecske, amely akkora méretű lenne, mint az elektron. A magok nem képződnének neutronok nélkül; így hasonlóan az elektronok sem alkotnak elektronmagot. Az elektronok közötti erős Casimir-vonzás a legjobb esetben is metastabil.

Az alapvető erők listája egyre hosszabb:

1. mechanikai erő,

2. elektromágneses erő,

3. gyenge erő,

4. erős erő,

5. sötét erő,

6. nagy energiájú gravitációs erő,

7. taszító erő elektronok és protonok között,

8. taszító erő az elektronok között,

9. taszító erő a protonok között,

10. taszító erő a protonok és a neutronok között,

11. taszító erő a neutronok között,

12. vonzóerő az elektronok között.

Itt van még valami elgondolkodtató. Ha figyelembe vesszük a Casimir-effektust, azt mondják, hogy a vákuum a lemezeket nyomja. A mélyebben felmerülő kérdés az, hogyan hatnak a vákuum-ingadozások? A válasz: az elektronok, protonok és a protonok és elektronok közötti taszító erők révén. A virtuális elektronok és/vagy protonok újra egymást taszítják, mikor közel érnek egymáshoz. A részecskék közötti taszító erő sokkal erősebb, mint az elektrosztatikus taszító erő.

Az az állítás, hogy az elektronokra nem hat az erős kölcsönhatás, hazugság. Olyan kölcsönhatásban vesznek részt, amely azonos az erős kölcsönhatással, de csak más elektronokkal.

90 R. Fleming „Casimir vonzása az elektronok között”

https://www.researchgate.net/publication/283795817_Casimir_Attraction_Between_Electrons

72. hazugság: Leptonok

A fizikában a 72. legnagyobb hazugság a lepton. A leptonok olyan ½ spinű részecskék, amelyek nem vesznek részt erős kölcsönhatásban. Hat részecske van meghatározva leptonként: elektron, müon, tauon, elektronneutrínó, müon-neutrínó és tau-neutrínó.

Rögtön két nagy problémát látunk a részecskék lepton osztályával kapcsolatban. Először is, a hat részecske közül öt nem elemi részecske. Még csak nem is szabad részecskéknek tekinteni őket, mivel két vagy három másik részecskéből állnak. Az egyetlen igazi részecske a csoportban az elektron.

A második probléma az, hogy az elektron erős kölcsönhatásba lép más elektronokkal. Ez az erős kölcsönhatás elvileg megegyezik a protonok közötti erős kölcsönhatással. Az a tény, hogy az elektronok és a protonok nem lépnek kölcsönhatásba egymással óriási méretkülönbségük miatt, nem elegendő egy új részecskeosztály létrehozásához.

A részecskék lepton osztálya a fizika egyik nagy hazugsága. Nem túl nagy merészség azt állítani, hogy a leptonok létezésének a védelme is hazugság. Az elektronok és protonok közötti erős erő hiánya nem teszi őket különböző típusú részecskévé, csak eltérő méretű részecskévé.

73. hazugság: A protonok nem elemi részecskék

A fizikában a 73. legnagyobb hazugság az, hogy a protonok nem elemi részecskék. A fizika egyik legnagyobb félreértése, amely rossz irányba terelte a részecskeelméletet, az volt, hogy mivel a protonoknak szerkezetük van, nem lehetnek alapvető részecskék. Tehát az a gondolat, hogy bármiből is készül egy szerkezet, az alapvetőbb lenne magánál a részecskénél, téves érvelés, mivel lehetséges, hogy egy részecskének szerkezete van, de ez a szerkezet csak a részecske részeként létezik, ezért a részecske és a szerkezet együttvéve elemi. Hazugság azt állítani, hogy egy részecske csak azért nem elemi, mert szerkezete van.

Az interneten a legtöbb helyen három kvarkból álló protont láthatunk háromszögben. Amikor szóródási kísérleteket végzünk, nem ezt látjuk. A proton külseje gömb vagy kvázi gömb alakúnak tűnik. A proton belseje látszólag tele van kisebb részecskék sokaságával, amelyek virtuális kontinuumot alkotnak.

Richard Feynman olyan modellt talált ki, amely elég jól illeszkedik a szórási kísérletekhez. Modelljében a proton sok kisebb részecskéből áll, amelyeket partonoknak nevezett el. 91 E kifejezés alatt ezreket, esetleg 100 000-et vagy még többet értett. A proton úgy működik, mintha kisebb részecskék kontinuumából állna. Amint a kvarkelmélet elfogadott lett, Feynman elméletét választották, és azt mondták, hogy a partonoknak valójában kvarkoknak kell lenniük, azonban nem szabad elfelejteni, hogy a 3, mint mennyiség, sokban különbözik a 100 000-től.

A különbség kiegyenlítése érdekében a kvarkelméletek szerint sok gluonnak kell lennie, és a kvarkok sokat ugrálnak, tehát a proton maga gluonok és kvarkok felhőjének tűnik. Még virtuális kvarkpárokat is hozzáadtak a számok kiegészítéséhez. Miközben a fizikusok sokkal több szóródási adatot gyűjtöttek össze az elmúlt 50 évben, az alapvető kvark-gluon modell nem sokat változott.

De van egy probléma; a kvarkok és a gluonok nem valódiak. A kvark modellt azért találták ki, hogy egyszerűsítse a részecskeelméletet, de csak még bonyolultabbá tette. Ráadásul a kvark modell nem a legalapvetőbb rezonanciát, a semleges piont modellezi sok más mezon mellett. A kvark modell egy megbukott elmélet. Sőt, még ennél is rosszabb: számmisztika.

A gluonok természetesen nem valódiak, mert az erőátvitel mérőbozon részecskecsere-modelljének nincs értelme. Ez, és az erős nukleáris erő a részecskék közötti elektromágneses erőkölcsönhatásnak, az erős Casimir-erőnek tekinthető.

Visszatérve a Feynman-modellhez, még soha senki nem észlelt partont. Van azonban valami, amelynek száma jóval meghaladja a százezreket, és amelyről ismert, hogy létezik egy protonban, ez pedig a vákuum fluktuációja, és nem a kvark fajtája. Mivel nem valószínű, hogy két dolog százezret foglal el ugyanazon a kis helyen, Feynman partonjai valóban vákuum-ingadozások.

Minden arra mutat, hogy a protonok elemi részecskék, arra, hogy tartósan stabilak. A protonok nem bomlanak le normál időskálánkon, és az eddigi tudományos bizonyítékok alapján a proton felezési ideje meghaladja a 1034 évet. 92,93 A protonbomlás tehát hazugság.

Ha a protonoknak független létező szerkezetük lenne, a protonok lebomlanának. Ha egy proton szét tudna válni, akkor megtörténne. Mivel a protonok nem bomlanak le, a belső szerkezetüket úgy kell a protonhoz kötni, hogy az csak egy protonon belül forduljon elő, vagy esetleg egy hasonlóan tartósan stabil részecskében, mint például az elektronnál.

Milyen a proton szerkezete? Nem tudjuk. Mivel a proton tömege egy akkora Casimir-üregnek felel meg, mint a proton, úgy tűnik, hogy ez egy vákuum-ingadozásokkal teli üreg. Ahogy Dirac feltételezte az elektronról, úgy néz ki, mint egy buborék a nullapontos mezőben. Ezen kívül nem tudjuk, mi okozza a proton töltését, anyagát vagy antianyagát, mágneses terét vagy spinjét.

Ahogy az 55. hazugságban megemlítettük, az elektronokat tévesen kicsinek és szerkezet nélkülinek tartották. Ezek nyilvánvalóan hazugságok, mivel tudományosan nincs értelmük. Nem lehet fizikailag leírni egy részecske tömegét, töltését, anyagát vagy antianyagát, mágneses terét és/vagy spinjét valamilyen szerkezet nélkül.

Sokkal könnyebb lenne kideríteni a két tartósan stabil elemi részecske szerkezetét, ha a fizikusok a kettő közül a nagyobbik elemzésére összpontosítanának a kisebbik helyett. Sajnos a 10-12 méteres léptékű elektronszórási kísérletek területét elhanyagolták. Még tisztességes becslést sem ismerünk az elektron töltési sugarára, még kevésbé sejtjük a szerkezetét. Ezek a kísérletek sokkal olcsóbbak és könnyebben kivitelezhetőek lennének, mint a legtöbb ma folyó részecskekísérlet, és meg is érdemelnék.

Az az állítás, hogy a protonok nem elemi részecskék, hazugság. Egy nap, miután a fizikusok erőfeszítéseket tesznek az elektron szerkezetének vizsgálatára, rá fogunk jönni, hogy a protonok ugyanazok, csak kisebbek; legalábbis ez a jóslatom.

91 R. P. Feynman, R. P., "The Behavior of Hadron Collisions at Extreme Energies". High Energy Collisions: Harmadik nemzetközi konferencia Stony Brook-ban, N.Y. Gordon és Breach. 237–249., 1969.

92 B. Bajc, J. Hisano, T. Kuwahara, Y. Omura, "Küszöbkorrekciók dimenziós hat protonbomlási operátorokhoz nem-minimális SUSY SU(5) GUT-okban". Nukleáris fizika B. 910: 1, 2016, arXiv:1603.03568.

93 H. Nishino, Super-K Collaboration, "Proton Decay keresése p+→ e+ π0 és p+→ μ+ π0 segítségével egy nagyvízi Cserenkov-detektorban". Fizikai áttekintő levelek. 102 (14), 2012.

74. hazugság: A neutronok nem elektronok és protonok

A fizika legnagyobb hazugságai közül a 74. az, hogy a neutronok nem elektronok és nem protonok. A neutronok akkor keletkeznek, amikor egy elektron legyőzi a közötte és a proton közötti potenciálgátat, és egyesül a protonnal. Ezután egy szabad neutron protonná és elektronná bomlik le, felezési ideje valamivel több, mint 10 perc. Vegye figyelembe, hogy a neutronok sokkal stabilabbnak tűnnek, ha protonokkal és más neutronokkal körülvett atommagban vannak. Valójában nem stabilabbak, mivel a neutronok folyamatosan bomlanak, miközben új neutronok keletkeznek.

Mint más kombinációs részecskék vagy rezonanciák esetében, a bomlástermékek adják a legjobb támpontunkat a összetételükhöz. Következésképpen a legjobb működő hipotézis az, hogy a neutron egy proton és egy elektron kombinációja, mivel nem bomlanak le kvarkká vagy bármi más, ami kimutatható. Ugyanakkor szem előtt kell tartanunk, hogy a neutronok sokkal kisebbek, mint egy Compton hullámhosszú elektron, ezért az elektront valamilyen módon át kell alakítani.

Három dolog akadályozta az elektron plusz proton modellt a neutron esetében: a proton szerkezete, a lepton megmaradása és a kvark modell. Azt találták, hogy a protonoknak van szerkezete, míg az elektronoknak nincs szerkezetük. Ezt követően a fizikusok elfogultak amellett, hogy hamisan azt gondolták, hogy a neutronok is valami elemibb anyagból állnak, ugyanakkor elutasították, hogy az elektron része ennek a szerkezetnek.

A második probléma az volt, hogy mivel a fizikusok nem értették a neutronok bomlását, feltalálták a neutrínót, hogy elvigyék a bomlási folyamatból származó felesleges energiát. Aztán feltaláltak egy szabályt ezeken a nem megfigyelt neutrínókon, az úgynevezett lepton-megmaradást.

A lepton-megmaradásban össze kell adni a leptonok számát a bomlási egyenlet mindkét oldalán, ahol az antianyag leptonok negatívak, és meg kell győződni arról, hogy egyenlők. Mint korábban említettük, mivel a leptonok nem valódiak, a lepton-megmaradás nem valós. Ennek ellenére a szabad neutron standard bomlási egyenlete a 74-1 egyenletben látható.

74-1 egyenlet

Ebben az egyenletben az elektron és az anti-elektron neutrínó kioltódik, így nulla nettó lepton van az egyenlet mindkét oldalán, és a lepton megmarad. A lepton-megmaradás törvényét beleverik a fizikus hallgatók agyába, így az az elképzelés, hogy a neutron egy protonból és egy elektronból áll, nagyrészt eltűnt.

Nagy a valószínűsége annak, hogy a neutrínók saját antirészecskék, akár összetettek, akár nem. Tehát honnan kellene tudnunk, mikor kell kivonni egy neutrínót, vagy mikor kell hozzáadni egy neutrínót? Gondolkozz el róla. Mindenesetre nem kívánatos a lepton-megőrzés alapelvként való megtartása, különösen mivel definíció szerint nincsenek is leptonok.

A neutronbomlás során valójában az történik, hogy egy virtuális elektron-pozitron pár kölcsönhatásba lép a neutronnal. A virtuális pozitron a neutron elektronrészével megsemmisül, és egy protont és egy egykor virtuális, de most szabad elektront hagy maga után. Így halad át az elektron a potenciálgáton, ami nem igazán alagút.

Ezt az egyenletet a 74-2 egyenlet mutatja.

74-2 egyenlet

A valóságban úgy néz ki, hogy az elektron nem távozik, ha egy neutron belsejében van, csak valamilyen módon átalakul. A fizikusok más kitalált szabályokat is felállítottak, amelyek akadályozzák a valós részecskefizika megteremtését, de ezekre most nem térünk ki. Elég azt tudni, hogy a részecskék nem ismerik ezeket a szabályokat, és a fizikai korlátaik alapján működnek.

Ami a harmadik problémát illeti, a kvarkokról valójában semmi továbbit nem kell elmondani. Ez egy hamis numerológiai modell, amelyet el kell vetni.

Ez azt jelenti, hogy a neutron egy protonból és egy elektronból álló összetett részecske. El tudjuk képzelni, milyen lehet. Mivel a neutron mérete hasonló a protonhoz, a neutron ugyanazt a tömegszabályt követi, mint a proton. Tömegét az a vákuumenergia határozza meg, amelyet Casimir-üregként kezelve kizár. Ez azt jelenti, hogy az elektronnak zsugorodnia kell méretében, lényegében a proton szerkezetére zuhanva. Annak megállapításához, hogy ez pontosan hogyan működik, fel kell venni valakinek az elvégzendő teendők listájára.

Mindhárom részecske, az elektron, a proton és a neutron szerkezete tele van vákuum-ingadozásokkal. Valaminek kell lennie a szerkezetükben, ami lehetővé teszi számunkra, hogy a részecskéket a vákuum-ingadozások gyűjteményének tekintsük, amikor szórási kísérleteket végzünk. A részecskék szerkezete arra készteti őket, hogy a Feynman által a parton modelljében leírt módon kölcsönhatásba lépjenek. Valami a szerkezetben kimutathatóvá teszi a vákuum ingadozásait, körülbelül úgy, ahogy egy léggömb érzékelhetővé teszi a benne lévő gázt.

Az a hipotézis, hogy a neutronok nem proton plusz elektronból állnak, hazugság. Bár a neutronok, a protonok és az elektronok szerkezetének vizsgálata ezen a ponton teljesen spekulatív, egyértelmű, hogy a továbbiakban a neutronokat protonok és elektronok kombinációjaként kell kezelni, és látni kell, hogy ez hová vezet.

75. hazugság: A részecskéknek relativisztikus tömegük van

A fizikában a 75. legnagyobb hazugság az, hogy a részecskéknek relativisztikus tömegük van. A relativisztikus tömeg az a koncepció, amely szerint a dolgok tömegenergiát nyernek, ha növelik a sebességet. Ez egy relativisztikus hatás, mint az óra lassulása, és ugyanazt a kifejezést használják a nyugalmi tömeg- vagy energiaegyenlet nevezőjében (75-1. egyenlet), mint korábban a távolságra és az órajelre vonatkozóan láttuk.

75-1 egyenlet

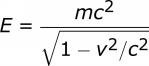
A zavarba ejtő kérdés ezzel kapcsolatban: mit jelent ez a részecske szerkezetére nézve? És: valóban növekszik a részecske tömege, vagy valami más történik? Az éter-elutasítók itt ragadtak le, mivel nullpontenergia megléte nélkül egy részecskére vonatkozóan leragadtak abban a gondolatban, hogy a részecskék valójában nehezebbekké válnak.

Ami még rosszabb, mivel hisznek a hosszösszehúzódásban (14. hazugság), azzal a gondolattal szembesültek, hogy minden fizikai méretű részecske rövidebb lesz a sebesség irányában, tehát ha gömb alakúnak indulna, akkor végül palacsinta alakú lesz, ahogy megközelítette a fénysebességet.

Akkor felmerül a kérdés, hogy a részecske nagyobb vagy kisebb lesz? Végül úgy döntöttek, hogy pontként kezelik a részecskéket (54. hazugság), hogy elkerüljék ezeket a szerkezeti kérdéseket. Ha tényleg van bátorsága, próbálja meg kitalálni a részecske szerkezetét a speciális relativitáselmélet segítségével, amikor nincs szabványos referenciakeret, és így nincs mód arra, hogy megmondja, melyik megfigyelőnek kell gömb vagy éppen palacsinta alakú részecskét látnia.

Kiderült, hogy van más megoldás is, és ehhez éter kell. Ha felidézzük a tehetetlenség leírását a 22. hazugságból, akkor a tehetetlenség a vákuum fluktuációs dipólusok forgásából adódik. Ez a forgás egy mozgó töltés körüli mágneses térhez hasonló mező kialakulásához vezet, de ebben az esetben a mechanikai dipólussal, az anyaggal és az antianyaggal való kölcsönhatások miatt következik be. E mágnesszerű mechanikai tér és a mozgó anyagtest kapcsolata az önindukció szabályait követi. A test mozgása a mező kialakulását, a mező pedig a test mozgását idézi elő.

A mozgó test kinetikus energiájának fele a mezőben van, bár a fizika matematikában hagyományosan figyelmen kívül hagyják. A kinetikus energia képlete E = ½mv2, míg valójában csak E = mv2 . Ez azt jelenti, hogy mindaddig, amíg következetesen figyelmen kívül hagyjuk az energia felét, a matematika jól működik. Vegye figyelembe, hogy eredetileg ugyanazt a logikát használták az E = mc2 egyenlet igazolására a nyugalmi tömegre. A tehetetlenségi modell alapján az összes tehetetlenségi és mozgási energia valójában az étermezőben van.

Ha a részecske tömegéről van szó, valami hasonló van. A részecske csak akkor van igazán nyugalomban, ha az éter-nyugalmi állapotban van. Minden más vonatkoztatási rendszerben a vákuumhoz viszonyított sebessége van, és ez a sebesség a mágneses-szerű mechanikai tér energiájának növekedéséhez vezet. A mágnesszerű mechanikai térenergia a relativisztikus tömegenergia.

A „relativisztikus tömeg” a mezőben van, nem a részecske, és ez energia, nem tömeg. Emlékezhetünk arra is, hogy a hossz-összehúzódás hazugság, így nem kell fizikai palacsintaeffektussal foglalkoznunk, egyszerűen nem történik meg. A részecske szerkezete mindig ugyanaz, függetlenül a részecske sebességétől. És mivel a részecske tömege is nullponti energia, minden tömeg, legyen az relativisztikus vagy más, nullaponti energia. Az az elképzelés, hogy a részecskéknek relativisztikus tömegük van, hazugság. Az éter, a nullpont mező hordozza azt a többletenergiát, amelyet helytelenül „relativisztikus tömegnek” nevezünk. Ebből a szempontból a relativisztikus tömeg kifejezés is hazugság. Csak relativisztikus energiának kellene nevezni.

76. hazugság: A tömeg a Higgs-mezőnek köszönhető

A fizikában a 76. legnagyobb hazugság a tömeg a Higgs-mezőnek köszönhető. Peter Higgs, François Baron Englert és Robert Brout azzal az ötlettel álltak elő, hogy a tömeg egy új típusú mezőből származik, amelyet ma Higgs-mezőnek hívnak, és ez az új mező a Higgs-bozonnak köszönhető. 94,95 Ez a munka fontos volt, mivel Diracon kívül egyetlen standardmodell-fizikus sem tudta a választ arra a kérdésre, hogy honnan jön a tömeg? Amint azt már a 19. hazugság tárgyalja, a tömeg nem eredendő belső tulajdonság. Ez különösen fontos volt a gyenge kölcsönhatás-elmélet szempontjából, mivel nem ismert, hogy a W és Z részecskék hogyan juthatnak ekkora tömeghez. Miután bejelentették a Higgs-bozon felfedezését, Higgs és Englert elnyerte a Nobel-díjat.

A Higgs-hipotézis jól ismert esete a fizikusok állandó modus operandijának, amikor új dimenziót, mezőt és/vagy részecskét találnak ki, mikor nem tudják, hogyan működik valami fizikailag. A fizikusoknak volt már, mint más fajta terek, nullponti mezője, elektromágneses mezője, fotonmezője, neutrínomezője, gluonmezője, gravitonmezője, a gravitációs hullámokról és kozmikus háttérsugárzásról már nem is beszélve. De miért nem találunk ki új mezőt a tömeg meghatározására?

Az előző fejezetekben kimutattuk, hogy a fizika összes energiatere a nullaponti mezőre redukálódik, így nem nehéz elképzelni, mi történik a Higgs-mezővel, különösen azért, mert a tömeg eredetére van jobb magyarázat. Az elektronok, protonok és neutronok tömege nem a Higgs-mező miatt létezik. Ezen részecskék tömege azoknak a részecskéknek köszönhető, amelyeknél ha nincs nullponti energia, akkor egyenlő a tömegükkel. További részletekért tekintse meg a 19. hazugságról szóló fejezetet és az erre hivatkozott dokumentumot 37

Az instabil részecskék, amelyeket pontosabban rezonanciáknak neveznek, némileg eltérőek. A pion, müon és tauon alapvető Sternglass modelljei az 59., 62. és 63. hazugságban láthatók. Az elektronhoz és a protonhoz hasonlóan tömegük megegyezik az általuk kizárt vákuumenergia mennyiségével, azonban ez a kizárás nem mind gömb alakú üreg formájában történik.

A rezonanciák tömege több részből áll. Míg a vákuum-ingadozásoknak nincs tömegük, ha a vákuum-ingadozás a Heisenberg-féle határozatlansági elv által megengedettnél hosszabb ideig fennáll, akkor az alkotó részecskéknek normál nyugalmi tömegenergiájuknak kell lenniük. Következésképpen a pionban, müonban és tauonban lévő elektronok és pozitronok normál nyugalmi tömege 511 keV/c2. Ez a nyugalmi tömeg a Casimir-üregüknek köszönhető.

Mivel a Sternglass-modell egy relativisztikus modell, amelyben az alkotó részecskék gyorsabban mozognak, mint a fénysebesség, ezeknek is van „relativisztikus tömegük”. A „relativisztikus tömeg” azonban nem a részecske és a Casimir-üreg méretének változásából adódik. A „relativisztikus tömeg” a tehetetlenségi energia, amely az inerciális nullponti mező forgó vákuum-ingadozásaiba esik.

A szögimpulzus és a mágneses mezők miatti kisebb tömeg-energia-hozzájárulás hasonlóképpen a vákuum-ingadozások energiájának köszönhető, amelyek ezeket a mezőket alkotják.

Az összes rezonancia tömege szintén az ideiglenesen gerjesztett részecskék nyugalmi tömegének, valamint a relativisztikus tömegüknek, más inerciális „tömegeinek” és a rezonanciaterekből származó tömegenergiának a kombinációjából adódik. Ezen tömegenergia-források mindegyike kiszorítja a vákuumenergiát. A rezonanciák és a részecskék tömegenergiájának minden formája a vákuumenergia elmozdulásának köszönhető.

A Higgs-mezőnek köszönhető tömeg hazugság. A tömeg nem a Higgs-mezőnek köszönhető, hanem a nullapontos mezőnek.

94 F. Englert, R. Brout, "Broken Symmetry and the Mass of Gauge Vector Mesons." Fizikai áttekintő levelek. 13 (9): 321–323, 1964.

95 P. W. Higgs, "Broken Symmemetries and the Mass of Gauge Bosons". Fizikai áttekintő levelek. 13 (16): 508–509, 1964.

A fizika legnagyobb hazugságai közül a 77. a Higgs-bozon.

Az elmúlt években sok tudományos hír jelent meg a CERN nagy hadronütköztetővel kapcsolatos kísérletről, amellyel a feltételezett Higgs-bozont keresték. A fizikusok bejelentették, hogy ezt 2012 júliusában találták meg. A Higgs-bozon felfedezése a mainstream fizikusok szerint megerősíti a Higgs-mező létezését és megoldja a tömegkérdés eredetét. Természetesen szokás szerint tévedtek.

A fizikusok egy statisztikailag alig szignifikáns csúcsot fedeztek fel adataikban körülbelül 126 GeV energiánál. Ennek a csúcsnak nem volt elektromos töltése, 0 spinje és egyéb olyan tulajdonsága, amelyek megegyeztek a hipotetikus Higgs-bozonnal. Alapvetően tehát minden olyan tulajdonsággal rendelkezik, amelyet egy rezonáns vákuum-ingadozástól elvárhat az ember; más szóval semmi megkülönbözteti meg attól. Különös szakításként a múlt fizika kísérleti protokolljával, a Higgs-bozont anélkül fogadták el, hogy ezt egy másik laboratórium külön megerősítette volna.

A Higgs-felfedezés folyamatának tudományos integritásának hiányáról dokumentumok, sőt, egy könyv is született: Dr. Alexander Unzicker ’A Higgs-hamisítvány – Hogyan bolondították meg a részecskefizikusok a Nobel-bizottságot’ (The Higgs Fake – How Particle Physicists Fooled the Nobel Committee) című könyve erősen ajánlott a Higgs-kísérlethez kapcsolódó problémák jó összefoglalásaként. Ám még az sem biztos, hogy a CERN statisztikai adatkezelése helytálló volt, hiszen senki sem végzett független elemzést a Higgs-bozon-mérés adatairól. Dr. Unzicker ugyanakkor joggal kritizálja a kvarkelméletet és a tudomány jelenlegi világának a módszertanát általában.

Mégis a Higgs-bozon felfedezése elvetésének elsődleges oka az, hogy a Higgs-bozon a Higgs-mezővel együtt szükségtelen. A részecskék tömege a nullponti mezőnek köszönhető. A tömeg megegyezik a részecske vagy rezonancia által kizárt nullponti energiával. A Higgs-hipotézisre ezért egyszerűen nincs szükség.

Feltehetjük tehát a kérdést, ha feltételezzük, hogy ez a statisztikailag alig szignifikáns csúcs a nagymértékben manipulált adatokban valós-e, és egy napon megerősítik, hogy az-e, vagy más? Mint minden rezonancia esetében, a legjobb módja annak, hogy meghatározzuk, miből áll, ha megnézzük a bomlástermékeit. A CERN-kísérletekben azt gondolták, hogy a Higgs-bozon a négy lehetséges részecskepár valamelyikjére bomlik:

1. egy fotonpárra,

2. egy tauon és anti-tauon részecskepárra,

3. egy W + és W - részecskepárra,

4. Z bozonpárra.

Megjegyzendő, hogy a szakirodalom említ kvarkpárokat, de a kísérletek valójában nem mutatnak ki kvarkokat, ezért csak a valós fizikai bomlástermékeket, valamint a potenciálisan valós W és Z rezonanciákat fogjuk figyelembe venni.

Két foton nyilvánvalóan két elektron-pozitron párra. A tauon részecskepár gyorsan lebomlik egy elektron-pozitron párra plusz néhány „neutrínóra”. Ahogy korábban említettük, a W végül elektronná bomlik, plusz sok energiára, tehát egy W pár elektron-pozitron párt hoz létre. A Z-bozon végül egy elektron-pozitron párra bomlik, plusz sok energiára, így két Z részecske két elektron-pozitron párt ad.

Egy összetett modellben a Higgs-bozonnak legalább két elektron-pozitron párt kell tartalmaznia, amelyek közül legalább egy tau és antitau pár gerjesztett állapotban van. Tartalmazhat más rezonáns valós részecskepárokat is, például elektron-pozitron párokat. Erre néhány kreatív fizikus valószínűleg elég gyorsan rájön. Ami viszont fontos, az az, hogy ha valóban létezik rezonancia a 126 GeV energián, akkor legyen egy egyszerű módja annak, hogy két vagy több virtuális részecskepár gerjesztett állapotaiból álló rezonanciaként modellezzük.

Tehát a Higgs-bozon hazugság, és a Higgs-mező is hazugság. Valójában soha egyik hipotézisre sem volt szükség.

78. hazugság: A bozonok elemi részecskék

A fizika legnagyobb hazugságai közül a 78. a bozonok elemi részecskék. Aki fejben tartja a számot, az már rájön, hogy a standard modellben minden elemi bozon hazugság. Vannak azonban olyan összetett részecskék és atomok, amelyek bozonként viselkednek, és a Bose-Einstein statisztikát követik, de ezek nem elemi részecskék. A standard modell elemi bozonok listája a következőket tartalmazza:

1. foton – 4. hazugság

2. graviton – 49. hazugság

3. W & Z bozon – 68. hazugság

4. gluon – 70. hazugság

5. Higgs-bozon – 77. hazugság

A fotonok virtuális dipólusok sorozata, a hullámot alkotó vákuum-ingadozások mezőjével kombinálva. Noha összetett részecskékről van szó, a fotonok még mindig fontos energiahordozók.

A gravitonok kitaláltak. A nagyenergiájú gravitáció egy Fatio-Casimir erő, amely összhangban van a van der Waals erőkkel az elektromágneses és mechanikai erőelméletben.

A W és Z bozonok, ha léteznek, bomlástermékeik alapján összetett részecskék. Tömegüknél fogva nem működhetnek mérőbozonként anélkül, hogy megsértenék az energiamegmaradás elvét. A W és Z részecskék láthatóan nem szolgálnak valódi célt.

Az erős nukleáris erő könnyen tekinthető erős Casimir-erőnek, amely összhangban van az elektromágneses elmélettel. Ennek semmi köze a kitalált gluonhoz.

A Higgs-bozon, ha egyáltalán létezik, bomlástermékei alapján szintén összetett részecskének tűnik. Ennek a rezonanciának nem volt más értelme, minthogy a tömeg eredetét fölöslegesen megmagyarázza.

A 18. hazugságból azt is felidézhetjük, hogy a teljes mérőbozon, az intelligens csererészecske hipotetikus fikció. Egyszerűen nem tudja figyelembe venni az erőátvitelt és az erők miatti gyorsulást.

Az az állítás tehát, hogy a bozonok elemi részecskék, hazugság. Mindegyik vagy összetett részecske, vagy csak tisztán kitalált.

79. hazugság: Az elemi részecskék táblázata

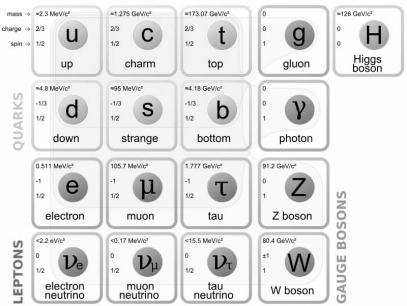
A fizika legnagyobb hazugságai közül a 79. az elemi részecskék táblázata.

Csak nézze meg a fenti táblázatot. Hol kezdjük? Őszintén, mennyire tévedhet egy modell és sok ezer fizikus egyszerre? Csak egy tartósan stabil részecske van, egy igazán elemi részecske az egész táblázatban. A többi vagy rezonancia, vagy pusztán kitalált.

A kategóriák önmagukban, kvarkok (61. hazugság), leptonok (72. hazugság), mérőbozonok (78. hazugság) külön hazugságok. A kvarkoknak és mérőbozonoknak nevezett rezonanciák nem töltik be meghatározott funkciójukat, vagy kitaláltak őket. A mérőbozonok külön-külön hazugságok, amint azt az előző fejezetben tárgyaltuk.

A neutrínók (64. és 65. hazugság) mint csoport hazugság, mivel mindegyik funkcionálisan vagy virtuálisan részecskepár, vagy egy kölcsönhatásból visszamaradt virtuális részecskepárok sorozata. Nincs tömegük, ahogy a fotonoknak sincs tömegük (66. hazugság).

A müon és a tauon sem elemi részecskék (62. hazugság és 63. hazugság). A müonra több mint 50 éve létezik egy modell, amelyet a standard modellfizikusok széles körben figyelmen kívül hagynak, és a tauonról könnyen bebizonyosodik, hogy egy hasonló típusú rezonáns összetett részecske. Ezeket a modelleket módosítani kell, de a müon és a tauon nyilvánvalóan nem alapvető részecskék.

Mindezen hazugságok után a fizikusok kihagytak egy részecskét annak a téves feltevésnek köszönhetően, hogy egy szerkezettel rendelkező részecske nem lehet elemi. Minden részecske, amely valódi részecske, és rendelkezik a szokásos részecsketulajdonságokkal, nem lehet pontrészecske (54. hazugság). Következésképpen fizikai méretekkel és szerkezettel kell rendelkezniük. Ezt bizonyítja az a tény, hogy a proton tömege megegyezik az ismert méretű gömbszerkezet által kizárt vákuumenergiával. A proton, az egyetlen másik tartósan stabil részecske az elektron mellett, elemi (a 73. fejezetből).

A fizika alapvető elméletéhez csak két elemi részecskére van szükség, az elektronra és a protonra, valamint ezek antianyag analógjaira, a pozitronra és az antiprotonra.

Az elemi részecskék szabványos modelltáblázata hazugság. Elkészíthetnénk a tényleges táblázatot, de egy két részecskés elemi részecsketáblázat butaságnak tűnne.

* Public Domain kép: MissMJ – Saját munkája a feltöltőtől, PBS NOVA [1], Fermilab, Tudományos Hivatal, Egyesült Államok Energiaügyi Minisztériuma, Részecskeadat-csoport)

80. hazugság: Koppenhágai értelmezés

A fizikában a 80. legnagyobb hazugság a koppenhágai értelmezés. A fizika legnagyobb hazugságainak gyűjteménye nem lenne teljes az elektrodinamika kvantummechanikai modelljének statisztikai bizonytalanságaiból kibontakozó hipotetikus elképzelések némelyikével. Mint annyi más hazugságnál, ez is annak köszönhető, hogy a fizikusok figyelmen kívül hagyták az étert.

A koppenhágai értelmezés egy iskola a kvantummechanikában elért eredmények értelmezésével kapcsolatban. Ennek az informális iskolának az úttörői Neils Bohr és Werner Heisenberg voltak, akik mindketten a Koppenhágai Egyetemen kutattak. 96,97

Az értelmezés összhangban van Heisenberg határozatlansági elvével és az ahhoz kapcsolódó megfigyelő által okozott hatásával. Elve szerint bizonyos tulajdonságpárokat, mint például a helyzetet és a lendületet nem lehet egyszerre ismerni. A megfigyelő effektus azt mondja ki, hogy a méréseket nem lehet a rendszer befolyásolása nélkül elvégezni. Ezért ha egy kvantumrendszer két komplementer tulajdonságának egyikét mérjük, a másik ismeretlen lesz.

A koppenhágai értelmezés egy lépéssel tovább viszi a megfigyelő hatását, és azt mondja, hogy egy kvantumrendszerben, ahol egynél több eredmény valószínűsége van, a megfigyelés vagy különösen a mérés révén megtörténik az egyik eredmény. Megjegyzendő, hogy ebben az esetben a megfigyelő bármely klasszikus rendszeren kívüli lehet, bár ez a klasszikus rendszer úgy is viselkedhet, ahogyan azt általában a kvantumelméletben megtörténik.

Egy másik megfogalmazási mód az, hogy egy kvantumrendszert egy hullámegyenlet ír le, amely különböző események bekövetkezésének valószínűségeinek eloszlását adja meg. Amikor a rendszert mérik, az interferencia hatására a hullámegyenlet összeomlik, és egyetlen eredményt ad. Vegye figyelembe, hogy a tudósok végtelenségig vitatkoztak arról, hogy mit is jelent valójában a koppenhágai értelmezés, beleértve Bohr-t és Heisenberget is, ezért nyugodtan tanulmányozza át, és gondolja át az értelmezést a továbbiakban.

Einstein és mások az évek során megkérdőjelezték a koppenhágai értelmezést, és Einsteint átfogalmazva, az univerzum nem kockajátékos. Einstein, mint éter-elutasító azonban nem engedte meg magának, hogy megfelelően használja a szükséges eszközöket, hogy megfelelően megtámadja ezt az elképzelést.

Az egyik versengő értelmezés a De Broglie-Bohm elmélet. 98 Ebben az elméletben valójában létezik egy konfiguráció, amely magában foglalja az összes részecskét, még akkor is, ha nem láthatók, és ezek a részecskék és mezők határozzák meg, hogy mi lesz az eredmény. Ez nagyon úgy hangzik, mintha a nullapontos mezőt írnák le. A De Broglie-Bohm modellben még mindig úgy gondolják, hogy a részecskéknek ez a láthatatlan mezeje leírható egy még nagyobb, mindenre kiterjedő hullámegyenlettel.

Tudjuk, hogy létezik a nullapont mező. A nullpont mező elvileg leírható egy nagyobb, mindenre kiterjedő hullámegyenlettel. Erre azért lenne szükség, hogy átfogó modellt kapjunk, jóllehet igen nagy kihívást jelentő feladat.

Az egyéni vákuum-ingadozásokkal való kölcsönhatások határozzák meg végső soron, hogy mi történik, az 57. fejezetben leírt módon. A virtuális részecskepárok kölcsönhatásba lépnek a részecskékkel, a fotonok pedig a részecskékkel, megsemmisülés-létrejövés kölcsönhatások révén. Míg a vákuum-ingadozások eloszlásukat tekintve is valószínűségiek, az eredmények egy adott időpontban és időpontban kölcsönhatásba lépő egyedi vákuum-ingadozások megléte miatt következnek be.

A külső interferencia, például egy mérőkészülék által okozott hatás szükségtelen. Nem szükséges, mivel a vákuum ingadozások a folyamatosan kölcsönhatásba lépnek a részecskékkel. Bár minden bizonnyal igaz az is, hogy egy mérés interferálhat egy kvantumrendszerrel, és bizonyos eredményt hozhat, de egy eredményt külső beavatkozás nélkül is el lehet érni.

A koppenhágai értelmezés hazugság. Egy mindenre kiterjedő elmélet, amely magában foglalja a nullapont mezőt, jobban megfelel a De Broglie-Bohm elméletnek, és különösen a vákuum-ingadozások létezésének.

96 N. Bohr: „A kvantum-posztulátus és az atomelmélet legújabb fejlődése”, Nature, 121: 580–590, 1928.

97 W. Heisenberg, „Nyelv és valóság a modern fizikában”, 10. fejezet, 145–160. oldal, Physics and Philosophy: the Revolution in Modern Science, George Allen & Unwin, London, ISBN 0-04-530016 X, p. . 153, 1959.

98 D. Bohm, "A kvantumelmélet javasolt értelmezése a "rejtett változók" szempontjából I. Fizikai áttekintés. 85 (2): 166–179, 1952.

81. hazugság: Kísérteties akció távolról

A fizikában a 81. legnagyobb hazugság a kísérteties távoli cselekvés. Amikor a koppenhágai értelmezés ellen vitatkozott, Einstein Boris Podolskyval és Nathan Rosennel együtt az úgynevezett EPR paradoxonnal állt elő. 99 Ők találták fel a kvantum-összefonódás fogalmát. Két részecske összefonódhat úgy, hogy olyan tulajdonságuk legyen, amely kiegészíti egymást. Egy ilyen közös tulajdonság a spin, ahol a két részecske, specifikusan Fermionok, egyébként azonos állapotban ellentétes spinű orientációjú.

Az érvelés egyik változata szerint, ha két részecske összefonódik majd elválik, és az egyik részecskénél megmérünk egy tulajdonságot, például a spint, akkor azonnal megismerjük a másik tulajdonságát is. Továbbá a koppenhágai értelmezés szerint, ha az első részecske tulajdonsága, például a spin állapota nem ismert a mérésig, akkor a második részecskének a tulajdonsága azonnal be kell állnia erre, még akkor is, ha a részecskék távolabb vannak egymástól. Ez a hatás azonban megsérti az információ terjedésének feltételezett fénysebesség-határát. Einstein ezt a típusú kvantumkommunikációt kísérteties távoli akciónak nevezte.

Számos kísérletben azt találták, hogy a kvantum-összefonódás távolról kísérteties (azonnali) cselekvéshez vezet. Számos közlemény, népszerű tudományos magazin és blogcikk számol be ezekről a jelenségekről. Mindazonáltal mind a koppenhágai értelmezés, mind az információs utazás fénysebesség-korlátjának hívei úgy tesznek, mintha ez nem számítana.

Most lehet, hogy azon gondolkodik, hogy ha beigazolódott, hogyan hazugság? Nos, a hazugság hármas. A nyilvánvaló az, hogy semmiképpen sem kísérteties. Ez szintén nem távoli cselekvés, és nem a fizika elveinek megsértése. A tulajdonságot a nullpont mezővel való interakció is beállíthatta jóval a mérés előtt.

Emlékeztetve a 38-as hazugságra, az elektromos és mágneses mezők sokkal gyorsabban terjednek, mint a fénysebesség, így két kvantum-összefonódott részecske közvetlen kapcsolatban áll egymással oly módon, hogy lehetővé teszi bizonyos alapvető információk átvitelét sokkal nagyobb sebességgel, mint a fényé. És ez egyáltalán nem kísérteties.

Távolról nem történik művelet, mivel az információ a nullaponti mezőn keresztül kerül továbbításra. A sebességhatárt sem sértik meg, mivel az olyan alapvető információk, mint az elektromos és mágneses mezők, valamint – ma már tudjuk – a spinállapotokra vonatkozó információk a fénysebességnél sokkal nagyobb sebességgel terjedhetnek. Persze lehet, hogy az információnak egyáltalán nem kell a fénysebességnél gyorsabban haladnia, ha nullponti térkölcsönhatás határozta meg a részecskék szétválása előtti állapotát.

A kísérteties távoli hatás megléte hazugság. Ez normális fizika. Csak annyit kellett tennie, hogy az étert bele kell foglalni az elméletbe, és megérteni kissé valamit az erőátvitelről.

99 A. Einstein, B. Podolsky, N. Rosen: "Tekinthető-e teljesnek a fizikai valóság kvantummechanikai leírása?" (PDF). Fizikai áttekintés. 47 (10): 777–780, 1935.

82. hazugság: A sok-világ értelmezése

Schrödinger pedig 1952-ben Dublinban tartott egy előadást, amelyben egy ponton tréfásan figyelmeztette hallgatóságát, hogy amit mondani készül, „őrültségnek tűnhet”. Az is volt, mert amikor az egyenlete több különböző eseményt írt le, ezek nem alternatívák voltak, hanem valóban „egyidejűleg” történtek. 100

Deutsch David, 2011

A fizikában a 82. legnagyobb hazugság a sok-világ értelmezése. A sok világ értelmezése nagy figyelmet kapott a népszerű tudományos cikkekben és televíziós műsorokban, valamint a tudományos-fantasztikus irodalomban, és leggyakrabban multiverzum-elméletnek nevezik. Ez egy alternatív ötlete a koppenhágai értelmezésnek, amely azon az elgondoláson alapul, hogy ahelyett, hogy csak egy valószínű eredmény történne, mind megtörténik, és minden más eredmény egy új világ vagy univerzum kialakulásához vezet.

Mint a fenti idézet is mutatja, Erwin Schrödinger volt az első, aki felvetette az ötletet, míg az első publikációt Hugh Everett írta 1957-ben, aki önállóan vetette fel az ötletet. 101 102 Az ötlet azonban csak akkor kezdett lendületet venni, amikor Bryce DeWitt kezdte nyilvánosságra hozni a sokféle világ értelmezését. 103,104,105

Szinte annyi multiverzum-modell létezik, mint ahány tudós és tudományos-fantasztikus író támogatja ezt az ötletet. A legtöbb ötlet annyira vad, hogy lehetetlen különbséget tenni tudományos-fantasztikus írók és tudósok között. Ez az egyik legrosszabb eset, amikor a fizika valódi tudományát sérti a sci-fi. A multiverzum-ötlet annyi könyv- és televízióbevételt hoz, mert őszintén szólva elég érdekes belegondolni, és nagyon népszerű a nagyközönség körében, de felbecsülhetetlen az a kár, amelyet a valós fizika integritásának okoz.

Az első probléma az, hogy minden egyes létrejött új univerzum súlyosan megsérti az energia-megmaradás elvét. A második az, hogy nincs hely, ahová elhelyezhetné. Igaz, hogy a fizikusok az extradimenziók fogalmát használják, hogy helyet találjanak neki, és ez hazugság, amivel egy későbbi fejezetben foglalkozunk majd.

A sokféle világértelmezés keretein belül létrejött új univerzumok száma túl nagy ahhoz, hogy elképzeljük. Gondoljunk arra a pillanatra, amikor egy elektron kering egy szénatommag körül. Nem igazán kering, hanem egy felhőszerű teret tölt ki, ahol a felhő méreteit statisztikailag leírják. Az elektron nem mozog folyamatos pályán, mert ez energiát veszítene. Ehelyett az elektronok diszkrét kis ugrásokat hajtanak végre egyik helyről a másikra, kvantumugrásokat, ahogy nevezik őket.

A mainstream fizikusok nem tudják leírni, hogy az elektronok hogyan hajtják végre ezeket a kvantumugrásokat, ezért azt feltételezik, hogy minden valószínűség lehetséges, és ezt valamilyen módon figyelembe kell venni. A problémájuk ismét az éter tagadására nyúlik vissza. Ha felismerjük, hogy az elektron körüli tér tele van éterrel, és különösen virtuális elektron-pozitron párokkal, nyilvánvalóvá válik, hogyan ugrálnak az elektronok az 57. fejezetben leírtak szerint.

Amikor egy elektron és egy pozitron találkozik, megsemmisítik egymást. De egy virtuális elektron-pozitron pár nem csak a párja másik felével semmisülhet meg; kereszt-megsemmisülhet egy másik vákuumelektron-pozitron párral vagy akár szabad elektronokkal. Az elektronok valójában nem ugrálnak, hanem valamivel távolabb egy új elektron keletkezik.

Attól függően, hogy hogyan mérjük a pozíciókat egy elektron által elfoglalt valószínűségi felhőben, potenciálisan végtelen számú lehetséges pozíció létezik. De mondjuk például felosztjuk a felhőrégiót egy 100 egységből álló kockára, amely millió lehetőséget ad. Akkor mondjuk, hogy az elektron másodpercenként milliószor ugrik.

Ha egy új univerzumot hoznak létre a millió lehetőség mindegyikére, amikor ez az egy elektron ugrik, akkor minden másodpercben egy billió (1000 milliárd) új univerzumot kellene létrehozni ahhoz, hogy a sok-világ értelmezés csak egyetlen elektronra is érvényes legyen.

Most szorozd meg ezt azzal a 1080 elektronnal, amely becslések szerint az ősrobbanás típusú univerzumban található, az érvelés kedvéért, majd szorozd meg ezt 13,8 milliárd évvel, még egyszer az érvelés kedvéért, majd duplázd meg, hogy a protonokat is beleszámold, és körülbelül 10110 univerzumot kapsz, amelyeket létre kell hozni. Ami lehetetlen. A sok-világ értelmezés így nyilvánvalóan egy nevetséges állítás.

Ehhez hozzá kell tenni, hogy a teljes feltevés helytelen, mivel a több valószínűség már nem létezik, ha az elektron ugrik. Az ugrás valódi fizikai folyamat, amelyet valódi fizikai vákuum-ingadozás közvetít. Míg a vákuumfluktuáció létezése valószínűségileg is leírható, de ha egyszer létezik és az elektron ugrik, akkor vége, egészen a következőig. A több eredmény nem jöhet létre. Ahogy a kvantumfizikusok mondják, a hullámfüggvény ezen a ponton összeomlik egyetlen eredményre. A többi valószínűség már nem lehetséges.

Minden más kvantumvalószínűségekkel leírt lehetőség hasonlóan determinisztikus. A vákuum fluktuációja, foton, elektron vagy más részecske a megfelelő helyen van a megfelelő időben ahhoz, hogy egy adott eredmény bekövetkezzen. A többi eredmény egyszerűen nem következik be. Ahogy a 80. fejezetben említettük, az éter fizikája összhangban van a De Broglie-Bohm értelmezéssel. Nem áll összhangban a koppenhágai vagy a sok-világ értelmezéssel.

Végül megfontolható az az érv, hogy egy alternatív világ vagy multiverzum soha nem észlelhető, mivel azok csak a mi univerzumunkon kívül létezhetnek. Nincs értelme a hülyeségekről spekulálni. Ez olyan, mint a filozófia vagy a vallás, és nem a tudomány.

A nem-űr hipotézishez hasonlóan a sok-világ és a több-univerzum hipotézisek nem tudományosak, mivel:

1. Nincs rájuk tárgyi bizonyíték.

2. Feleslegesek az univerzum leírásához.

3. Felesleges új bonyodalmakat adnak hozzá univerzumunk elméleteihez.

4. Soha nem észlelhetők.

A sok világ értelmezése és a kapcsolódó multiverzum-modellek mind hazugság. Egy univerzum van.

100 D. Deutsch, The Beginning of Infinity, Infinity, 310. oldal, 2011.

101 H. Everett, Theory of the Universal Wavefunction, Thesis, Princeton University, (1956, 1973), 1–140.

102 H. Everett, "A kvantummechanika relatív állapot-formulációja", Reviews of Modern Physics. 29: 454–462, 1957.

103 B. S. DeWitt: „Kvantummechanika és valóság: Az indeterminizmus dilemmájának megoldása lehet-e egy olyan univerzum, amelyben a kísérlet minden lehetséges eredménye ténylegesen megtörténik?” Physics Today, 23(9) pp 30–40, 1970. szeptember.

104 B. S. DeWitt, „The Many-Universes Interpretation of Quantum Mechanics”, Proceedings of the International School of Physics „Enrico Fermi” Course IL: Foundations of Quantum Mechanics, Academic Press (1972)

105 B. S. DeWitt, R. N. Graham, szerk., The Many-Worlds Interpretation of Quantum Mechanics, Princeton Series in Physics, Princeton University Press (1973).

83. hazugság: A kvantummechanika hullámmodellje

Planck képlete azt mondja nekünk, hogy a természetben ténylegesen előforduló „mező” valamilyen diszkrétséggel rendelkezik, ami részecskerendszerként viselkedik, ahol minél magasabb az oszcilláció frekvenciájának módja, amelyet a mező átengedhet magának, annál erősebben nyilvánulna meg ebben a részecskeszerű viselkedésben a mező energiája. 106

Roger Penrose, 2016

A fizika legnagyobb hazugságai közül a 83. a kvantummechanika hullámmodellje. A hullámmodellek a kvantummechanika alapját képezik, a kvantummechanika pedig hullámegyenleteket használ, hogy gyakorlatilag mindent leírjon a kvantumskálán. Az első hullámegyenlet a Schrödinger-egyenlet, amely a hidrogénatomot írja le. Egy másik híres hullámegyenlet az elektronokat leíró Dirac-egyenlet.

Amint azt az előző fejezetekben tárgyaltuk, a kvantummechanikai valószínűségek az alkalmazható hullámegyenlet által leírt lehetséges eredményeken alapulnak. Az eredmény állítólag akkor következik be, amikor a hullámegyenlet összeomlik. Tehát bárki, aki kvantumelméletet tanul, az egész tanulmánya során látni fogja a hullámot itt is meg ott is. Kvantummechanikai szempontból azt hihetjük, hogy a hullámtulajdonságok alapvetően valóságosak.

A hullámmodell az éter elutasítása miatt alakult ki, ami feltételé tette, hogy a részecske legyen részecske és hullám is. Ahogyan azt a 3. hazugságban tárgyaltuk, a hullám-részecske modell hazugság. A hullám az éter, nem pedig a részecske tulajdonsága. Továbbá az éter részecske-dipólusokból áll, így még a hullámok is valóban nagyon nagyszámú részecskék.

Ezek a vákuum-fluktuációs részecskepárok nagy számban felmérve hullámként hatnak, és a nullponti mező makroszkopikus tulajdonságai hullámfüggvénnyel írhatók le. A kvantummechanikai hullámegyenletek matematikai funkciójukat szolgálják, és lehetővé teszik számunkra a számítások elvégzését, de mikroszkópos léptékben az éter még mindig egy csomó részecskéből áll.

Ez azon alkalmak egyike, amikor a matematikai fizikusok azt akarják hinni, hogy egyenleteik a fizikai valóság alapvető leírásai, holott nem azok. A hullámegyenletek nem mások, mint matematikai eszközök. Nem állnak összhangban az a fizikai leírással, ami az éterben folyik.

Bár a részecskék leírhatók hullámegyenletekkel, amikor szórási kísérleteket végzünk, úgy viselkednek, mint egy csomó részecskével megtöltött tér, és azok a részecskék vákuum-ingadozások, amelyek részecskékből állnak. Egészen a legkisebb részekig részecskék vannak benne.

A kvantummechanika hullámmodellje hazugság. Jobb lenne, ha a fizikusok a hullámegyenleteket hasznos matematikai eszközökként kezelnék. Jó eszközök, mivel egy részecske alapú egyenletet nehéz felírni, ha lényegében végtelen számú részecskével van dolgunk, de mégis eszközök, nem pedig a természet elemi fizikai leírása.

106 Roger Penrose, Fashion Faith and Fantasy in the New Physics of the Universe, pg 192, Princeton University Press, 2016.

84. hazugság: A Kaluza-Klein elmélet

A fizikában a 84. legnagyobb hazugság a Kaluza-Klein elmélet. Hacsak nem tanult sok fizikát, lehet, hogy nem ismeri a Kaluza-Klein elméletet, de ez egy korai kísérlet volt két erő egyesítésére, és egyfajta előfutára a húrelméletnek. 107 108 109 A húrelmélet felülmúlta ezt, így a legtöbb fizikus valószínűleg azt gondolja, hogy ez régi hír.

A Kaluza-Klein elmélet jelentősége abban rejlik, hogy három új módszertant vezetett be két vagy több erő egyesítésére. Az első ilyen módszertan új dimenziót ad az elmélethez, hogy figyelembe vegye az erőt. Ebben az esetben az elektromágneses elméletet hozzáadták az általános relativitáselmélethez, így a 4 dimenziós általános relativitáselméletet 5 dimenziós elméletté változtatta, amely magában foglalja az elektromágnesességet is. Az általános relativitáselmélet 4 dimenziója tartalmazza a 3 fizikai dimenziót plusz az időt, amit extra dimenzióként kezelünk.

A második új módszertan az volt, hogy ahelyett, hogy az új dimenziót csupán matematikai módszertanként kezelték volna, úgy döntöttek, hogy az fizikailag valós. A gyakorlatban, ha egy N-dimenziós problémamegoldó tér van egy N-változós probléma megoldására, az rendben van. Ha azt gondolják, hogy az N dimenzió mind fizikailag valóságos, akkor bajba kerülnek.

A harmadik módszer az, hogy amikor szembesültek egy új fizikai dimenzióval, ami nem valós, úgy döntöttek, hogy fel kell csavarni, így valahogy el van rejtve a szem elől. Gyakori példa arra, hogy ennek hogyan kell működnie, a kerti tömlőmodell. A kerti tömlő távolról úgy néz ki, mint egy vonal, de közelről úgy néz ki, mint egy hengeres cső. Az extra fizikai dimenzió a Kaluza-Klein elméletben valahogy így van összegömbölyödve, tehát csak azt látjuk, hogy ez egy vonal.

Természetesen jó, hogy két erőelméletet kombinálhatunk egyetlen matematikai egyenlethalmazba. Még az egyik erőelmélet új matematikai dimenzióként való kezelése is ésszerű matematikai megközelítés a problémamegoldáshoz. Hazugság viszont azt állítani, hogy ez az új fizikai dimenzió lenne, amely valójában nem létezik fizikai dimenzióként, de valahogy fel van görbülve, és így nem látjuk. Ez az oka annak, hogy óvatosnak kell lennünk, amikor matematikusaink úgy tesznek, mintha fizikusok lennének.

A Kaluza-Klein elmélet megjósolja a gyenge és az erős erőt, így világossá vált, hogy ha valaki ezzel a megközelítéssel akarna egy egységes erőelméletet kitalálni, akkor még több láthatatlan dimenziót kell feltalálnia. A következő fejezetben ezt nézzük meg.

Végül nem kell új dimenziót kitalálnunk a gravitáció, az elektromosság és a mágnesesség egyesítésére. Az elektromágneses és mechanikai erőelméletből származó Fatio-Casimir effektus jó munkát végez a gravitáció számításában. A Kaluza-Klein elmélet inkább szükségtelen bonyodalma, semmint leegyszerűsítése az erőelméleteinknek.

A Kaluza-Klein elmélet hazugság. Ez egy szükségtelen és szükségtelenül bonyolult megközelítés a gravitáció és az elektromágnesesség egy elméletben való egyesítésére.

107 T. Kaluza, "Zum Unitätsproblem in der Physik", Sitzungsber. Preuss, Akad, Wiss, Berlin. (Math. Phys.): 966–972,1921.

108 O. Klein, "Quantentheorie und fünfdimensionale Relativitätstheorie." Zeitschrift für Physik A. 37 (12): 895–906, 1926.

109 O. Klein, "Az elektromosság atomitása mint kvantumelméleti törvény". Természet. 118, 516 (1926)].

85. hazugság: Húrelmélet

A fizikusokat általában nem aggasztják túlzottan a matematikai és ontológiai következetlenségek részletei, ha az elmélet megfelelő ítélőképességgel és körültekintő számítással alkalmazva továbbra is olyan válaszokat ad, amelyek a megfigyelés eredményeivel kiválóan egyeznek – gyakran rendkívüli pontossággal – finom és precíz kísérletekkel. A húrelmélet helyzete teljesen más. Úgy tűnik, hogy itt nincsenek olyan eredmények, amelyek kísérleti támogatást nyújtanának. 110

Roger Penrose, 2016

A fizikában a 85. legnagyobb hazugság a húrelmélet. A húrelméletben a részecskéket nem pontrészecskéknek, hanem húroknak tekintik. A részecskék tulajdonságait, például töltést, tömeget, spint ezután a húr tulajdonságainak tekintjük. Ez lényegében egy pontszerű részecskék tulajdonságainak tulajdonításának torz módja, míg a pontrészecske nem rendelkezhet semmilyen tulajdonsággal, sőt részecske sem lehet.

A húrelmélet fő problémája az, hogy nincs olyan, hogy húr. A húrkoncepció részecskemodellként való felfogása hazugság. Ezenkívül a legnépszerűbb húrelméleteknek 10 vagy 11 dimenziójuk van, és elég nehezen működnek; a matematikusoknak, akik kidolgozták a húrelméletet, van eszük azt hinni, hogy ezek az extradimenziók valósak.

Aztán kölcsönkértek egy oldalt a Kaluza-Klein elméleti játékkönyvből, és úgy döntöttek, hogy ezeket az extra dimenziókat valamilyen módon fel kell csavarni, hogy egyszerűen ne lássuk őket. Megjegyzendő, hogy sok mindent kihagytunk, hogy a legrosszabb részekre jussunk, így az olvasóra kell bízni, hogy tanulmányozza a húrelméletet, ha a számos, kicsit finomabb tévedést akarja tanulmányozni.

A húrelmélet különféle elméletekre ágazott el. Volt szuperszimmetrikus húrelmélet, amit szuper-húrelméletnek is neveznek, valamint számos más típus. Ezeket végül az M-elméletbe egyesítették. Aztán hozzáadták a D-Branes-t, hogy több Kaluza-Klein-szerű legyen a hipotetikus 11. dimenzió tömörítése. Ezek azonban hazugságok, minden csak hazugság.

Amint azt a szórási kísérletekből származó tudományos bizonyítékok mutatják, a protonoknak és elektronoknak van fizikai dimenziója. Amint a tömeglevezetés mutatja, ezek a méretek összhangban vannak a tömeggel és a részecskék gravitációs képességével.

A Dirac-egyenlet utalást ad arra, hogy mi lehet az anyag-antianyag, mivel matematikailag úgy néz ki, mint egy bivektor a geometriai algebrában, tehát úgy tűnik, hogy valamilyen módon kapcsolódik valaminek a részecskén belüli forgásához.

Igaz, hogy még nem tudjuk, hogy ezeknek a részecskéknek töltésük, spinük és mágneses nyomatékuk van, de valójában van esélyünk rájönni, ha egy háromdimenziós modellből indulunk ki.

Talán a töltés és még a spin is algebrailag további bivektorok, és ez talán egy valós fizikai részecskemodellhez vezethet.

Felmerül az a probléma is, amint arról az utolsó fejezetben szó lesz, hogy az erők könnyen egyesíthetők az elektromágneses és a mechanikai erőelméletben. Valójában nincs ok arra, hogy extradimenziókat adjunk hozzá az erők számbavételéhez, amelyeket már a kombinált elektromágneses és mechanikai erőelmélet részének kell tekinteni.

A legszomorúbb az emberi és fiskális tőke eltékozlása a húrelmélet hajszolása miatt. Dollár milliárdokat és több, mint ezer fizikus karrierjét pazarolták el ezekre a hülyeségekre. Sok racionálisan gondolkodó és zseniális fiatal fizikust eltérítettek el a valódi fizika kutatásától, és megrekedtek ezen az irracionális elméleti szinten. Mások, például jómagam, inkább az akadémiai fizikán kívüli életutat választották, ahelyett, hogy elképzeléseiket belefulladni látnák az irracionális fizikusok gondolatainak tengerébe.

A húrelmélet hazugság. Manapság a fizika legokosabb elméi közül sokan hajlandóak beismerni, hogy a húrelmélet nem valóságos, soha nem volt valóságos, és soha nem is lesz valódi. Itt az ideje, hogy a fizikus közösség jobb elméletekre fordítsa idejét és finanszírozását.

110 Roger Penrose, Fashion Faith and Fantasy in the New Physics of the Universe, pp 2-3 Princeton University Press, 2016.

86. hazugság: Extra fizikai dimenziók

A fizika legnagyobb hazugságai közül a 86. az extra fizikai dimenziók. Három fizikai dimenzióval rendelkező világban élünk. Ha előre tekintesz, és a szokásos módon leírod ezeket a dimenziókat, akkor az egyik dimenzió felfelé és lefelé, a másik oldalról oldalra, a harmadik pedig a tőled lévő távolság. Ezek kényelmes lineáris koordináták, amelyeket arra használunk, hogy megtaláljuk a mindennapi dolgokat, amelyeket látunk. Természetesen más háromdimenziós koordinátarendszereket is használhatunk, de három fizikai dimenzió a valóság. Az extra méretek fizikailag nem valósak.

Az üres tér, ha létezne ilyen, dimenzió nélküli lenne, mivel nem lenne benne semmi a távolságmérésre. A valós tér vákuumenergiát tartalmaz, a vákuum-ingadozásnak pedig hullámhossza és frekvenciája van. A vákuum-ingadozások hullámhosszai adják a tér méreteit. A frekvenciák adják a térnek az idő tulajdonságát.

A hullámhossz és a frekvencia nem ugyanaz, így a fizikai hossz és az idő sem ugyanaz. A főáramú modell tartalmaz egy négydimenziós téridőt, amely egyesíti a három fizikai dimenziót és az időt úgy, hogy négydimenziósként kezeli őket, de az idő még mindig különbözik a három fizikai dimenziótól, ahogy a frekvencia is különbözik a hullámhossztól. Ha valaki azt állítja, hogy az idő egy fizikai dimenzió, az hazudik.

Azt is fontos megjegyezni, hogy az éternek van egy nyugalmi állapota, ahol a vákuum ingadozása egyenletes. Az éter nyugalmi állapotában a fizikai méretek és a fizikai órajel egyenletes az egész univerzumban. Az éter méreteiben lapos és euklideszi, extra méretek nélkül.

Megjegyezzük, hogy itt vallásos hipotézissel állunk szemben, nem pedig tudományossal, ha:

1. Nincs rá tárgyi bizonyíték.

2. Az univerzumot felesleges leírni.

3. Felesleges új bonyodalmakat ad hozzá univerzumunk elméleteihez.

4. Soha nem lehet kimutatni.

Az extra fizikai dimenziók hazugság. Nem valódiak, nem szükségesek és még csak nem is tudományosak.

111 T. Kaluza, "Zum Unitätsproblem in der Physik". Sitzungsber. Preuss. Akad. Wiss. Berlin. (Math. Phys.): 966–972, 1921.

87. hazugság: A fénysebesség alapvető

A jövőben lesz olyan fizika, amely akkor működik, ha ħc/e2 értéke 137, és nem fog működni, ha más értéke van. (…) A jövő fizikája természetesen nem tekintheti alapvető mennyiségnek a három ħ, e és c mennyiséget. Ezek közül csak kettő lehet alapvető, a harmadiknak pedig ebből a kettőből kell származnia. Szinte biztos, hogy c egyike lesz a két alapvetőnek. A fénysebesség c olyan fontos a négydimenziós képben, és olyan alapvető szerepet játszik a speciális relativitáselméletben, korrelálja tér-idő egységeinket, hogy alapvetőnek kell lennie. 112

Paul Dirac, 1963

A fizika legnagyobb hazugságai közül a 87., hogy a fénysebesség alapvető. A fenti Dirac-idézet a fizika egyik fontos céljáról, az alapvető állandók számának csökkentéséről beszél. A 137-es érték természetesen a finomszerkezeti állandó inverzére vonatkozik. Úgy érezte, hogy a finomszerkezeti állandó mellett négy fontos állandó van az egyenletben, de csak kettő alapvető állandó.

Példaként említjük meg, hogy a standard modellben az alapvető állandók legnagyobb csoportja az összes részecske tömege, jelenleg 122 darab, és ez a szám folyamatosan emelkedik. Mivel nincs szabványos modellelmélet, amely fizikailag megmagyarázná ezeket a tömegeket, a mainstream fizikusok leragadtak a belső vagy alapvető tömegeknél. Ahogy a 19. hazugságban tárgyaltuk, a belső tömeg hazugság. Bármely elfogadható elméletben az összes jelenleg alapvető állandót az alapvetőbb tulajdonságokból kell származtatni.

A tömegre vonatkozó Dirac és Sternglass modellek lehetséges megoldásokat kínálnak erre a problémára, jelentősen csökkentve az alapvető állandók számát. A jelenlegi nem tömegelmélet tarthatatlan. A Sternglass-modell azt is elmondja, hogy a finomszerkezeti állandó inverze megegyezik egy relativisztikus elektron-pozitron pár energiájával MeV-ben. Ez egy fontos támpont, amely segít meghatározni a négy állandó közötti fizikai kapcsolatot.

Ahogy Dirac rámutatott, a fénysebesség szinte szentnek számít, mint alapvető állandó. A speciális és általános relativitáselmélet hipotéziseinek igaz hívei számára a fénysebesség állandósága és belső természete érinthetetlen.

Ha a fénysebesség nem alapvető állandó, akkor mindkét elmélet érvénytelen. Amint korábban említettük, helytelen gondolkodásuk az éter elutasításáig nyúlik vissza. Ha nincs éter, akkor a fénynek nincs közvetítő közege. Ha a fénynek nincs közvetítő közege, akkor a fénysebesség a fény belső tulajdonsága.

De a fénynek van egy közvetítő közege, ezért hazugság azt állítani, hogy a fény sebessége a fény belső tulajdonsága. A fénysebesség a közeg tulajdonsága. Ahhoz, hogy lássuk, hol ütközik problémákba a fényelmélet belső sebessége, csak meg kell néznünk a fénysebesség egyenletét az elektromos állandó (vákuum-permittivitás) és a mágneses állandó (vákuum-permeabilitás) szempontjából.

87-1 egyenlet

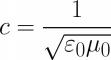
Azonnal látható, hogy az elektromos és mágneses állandók alapvetőbbnek tekinthetők, mint a fénysebesség. Az elektromos állandó az éter azon képességére vonatkozik, hogy lehetővé teszi az elektromos erővonalak kialakulását. Az éter azon képessége, hogy elektromos erővonalakat hozzon létre, és ennek a tulajdonságnak a korlátai a vákuum-ingadozások fizikai tulajdonságaiból fakadnak. Az elektromos állandó nem alapvető állandó. Hazugság azt állítani, hogy az elektromos állandó alapvető állandó. Az éterelutasítók viszont alapvető állandóként kezelik, hiszen nem hagytak maguknak más választást.

A mágneses állandó vagy vákuum-permeabilitás azzal függ össze, hogy az éter hogyan hoz létre mágneses teret elektromos áramok vagy mozgó elektromos töltések hatására. Ez a vákuum ingadozásának és mágneses mezők kialakításának képessége is. A mágneses állandó inkább származtatható állandó, nem pedig alapvető. Hazugság azt állítani, hogy a mágneses állandó alapvető állandó. Az éterelutasítók ismét kudarcot vallottak.

Az elektromos állandó az éter polarizálhatóságára vonatkozik, míg a mágneses állandó a vákuum-ingadozások forgási képességére vonatkozik. Mivel a polarizációhoz forgatás szükséges, mindkettő a nullapont mező elfordulásától függ. A vákuum fluktuációs dipólusok közötti Van der Waals erők határozzák meg ezeket a tulajdonságokat, különösen a van der Waals nyomatékot. A Van der Waals nyomaték ellenállást biztosít mind a lineáris, mind a forgó mozgással szemben. És képzeld el, a fénysebesség is az éter lineáris és forgó mozgással szembeni ellenállásának köszönhető.

Tehát nemcsak a fénysebesség származtatható az elektromos és mágneses állandókból, hanem a 87-1 egyenletben szereplő mindhárom úgynevezett alapállandó a vákuum van der Waals-féle nyomatékának különböző mértékét jelenti.

Visszatérve Dirac kijelentésére, kiderül, hogy a finomszerkezeti állandó nem pontosan a 137 inverze, így a miszticizmus egy része eltűnt. Ez egyszerűen egy újabb származtatott állandó, korlátozott mértékben használható, túl a részecskeelmélet szempontjából. Úgy tűnik, hogy mind a fénysebesség, mind az elektromos töltés (53. hazugság) egy napon alapvetőbb módon leírható.

Megjegyzendő, hogy csábító lesz e-t c-vel és c-t e-vel megoldani, de végső soron megoldást kell találni arra, hogy önállóan, vagy együtt oldjuk meg őket úgy, hogy mindkettőt korlátozza. Dirac által az idézetben tárgyalt négy állandó közül csak Planck állandója tűnik igazán alapvető állandónak. Még akkor is, ha egyszer lesz egy alapvetőbb fizikai leírásunk az energiára, akkor is találhatunk egy egyszerűbb levezetést a Planck-állandóra.

Az az állítás, hogy a fénysebesség alapvető fontosságú, hazugság. Ha elfogadjuk, hogy az éter a fény áteresztő közege, a fénysebesség ennek a közegnek, az éternek a tulajdonságává válik. Csak idő kérdése, hogy mikor vezeti le valaki a fénysebességet a vákuum-ingadozások közötti van der Waals-erők alapján.

112:00 Dirac, „The Evolution of the Physicist's Picture of Nature”, Scientific American, 1963. május, 208(5), 45-53.

88. hazugság: Gyorsabban, mint a fény

A fizika legnagyobb hazugságai közül a 88. gyorsabb, mint a fény. A fénynél gyorsabb utazás már régóta a sci-fi alapja. Enélkül a csillagközi űrutazás nem praktikus. Számos fizikus hódol a sci-fi rajongók fantáziájának azzal, hogy azon találgatnak, hogyan lehetne átlépni az anyagtestek fénysebesség-korlátját. És ők és médiaszervezeteik jócskán profitálnak belőle. Az ősrobbanás-modellben a fénysebesség megsértésének engedménye továbbtáplálta ezeket a fantáziákat.

Amint azt az előző fejezetekben tárgyaltuk, az erők terjedési sebességének sokkal nagyobbnak kell lennie, mint a fény sebességének, különben a pályák instabilak lennének. A távoli, úgynevezett fantom-hatás bizonyítéka azt is megkövetelheti, hogy az erők és a mezők sokkal gyorsabban terjedjenek, mint a fény.

Még az a gondolat is létezik, hogy a fény gyorsabban tud mozogni, mint a fény, ha egy megnyúlt Casimir-üregen keresztül jut át. Ezt Scharnhorst-effektusnak hívják, amelyet még nem ellenőriztek egyelőre de szerintem valószínűleg igaz lesz. 113 A Scharnhorst-effektus, akárcsak a Casimir-effektus, valószínűleg nem észlelhető rövidebb hullámhosszú fénynél olyan üregekben, amelyek távolsága egy mikronnál nagyobb. De előfordulhat, hogy nagyobb hullámhosszak, például mikrohullámok esetén az üregnek csak valamivel nagyobbnak kell lennie, mint a mikrohullámú sütő hullámhossza. Lehet, hogy ez az, ami az EmDrive-ban történik. Azonban, ha a Scharnhorst-effektust kísérletileg igazolják, akkor sem fogja az megengedni, hogy a nagy testek megsértsék a fénysebesség-határt.

Egyes sci-fi-írók és fizikusok azt feltételezik, hogy megzavarhatjuk a vákuumenergiát egy test előtt, és így gyorsabban haladhat. Mások azt feltételezték, hogy az egész hajót be lehet zárni, hogy elszigeteljük a tér éterétől, és így lehetővé tegyük, hogy a fénynél gyorsabban haladjon.

Ezekkel a fantasztikus ötletekkel kapcsolatos fizikai probléma a tehetetlenség eredetére vezethető vissza. A tehetetlenség a vákuumfluktuációs dipólusok forgásából adódik, amikor a test mozog a térben. Ezek a dipólusok nagyon kicsik lehetnek, így kitöltik az elektronok és az atommagok közötti teret. Némelyik olyan kicsi, hogy kitölti az atommagban lévő protonok és neutronok közötti teret, sőt még a protonokon, neutronokon és elektronokon belüli teret is. Nem kerülhető el tehát az a hatás, hogy a vákuum ingadozása ne korlátozza a mozgó test sebességét.

Azt is figyelembe kell vennünk, hogy egy köbcentiméter vákuumban a vákuumenergia legalább 1095 gramm tömegnek felel meg. Az egyetlen köbcentiméterben lévő energia sokkal nagyobb, mint a látható univerzum becsült nem vákuum energiája. Ha egy tudományos-fantasztikus író azt hiszi, hogy olyan rendszere van, amely elég energikus ahhoz, hogy manipulálja a vákuumot, akkor sajnos téved. Ahhoz, hogy ez még lehetséges legyen, először nagy mennyiségű vákuumenergiát kell tudnunk kinyerni közvetlenül a vákuumból. A nagy pedig azt jelenti, hogy sok nagyságrenddel nagyobb, mint a látható világegyetem összes tömege.

Talán a legszomorúbb látni azokat a tudományos-fantasztikus írók-fizikusokat, akik úgy gondolják, hogy valahogy meg tudjuk hajlítani magát a teret. Az űr túlságosan energikus ahhoz, hogy meghajlítsuk, még akkor is, ha ez fizikailag lehetséges lenne, de nem az. Erről a problémáról néhány fejezetben még lesz szó. És igen, a „warp drive+, a meghajlított téridő is hazugság. A fénynél gyorsabb utazás hazugság.

Egyszerűen nem lehetséges az anyagot elkülöníteni a nullpont mezőtől, vagy becsapni a nullapont mezőt, hogy megváltoztassa a nyugalmi állapotát. A fizikusok rossz szolgálatot tesznek a nyilvánosságnak és a tudománynak azzal, amikor együttműködnek ezzel a tudományos-fantasztikus ötletettel.

113 G. Barton, K. Scharnhorst (1993). "QED párhuzamos tükrök között: c-nél gyorsabb vagy a vákuum által felerősített fényjelek". Fizikai folyóirat A. 26 (8): 2037.

89. hazugság: Tachionok

A fizika legnagyobb hazugságai közül a 89. a tachionok. A tachionok olyan hipotetikus részecskék, amelyek a fénysebességnél gyorsabban mozognak. Különös tulajdonságuk, hogy a legkisebb sebességük a fénysebesség. A tachion olyan matematikai alkotás, amely a matematikai egyenletek normál fizikai határain kívül létezik. A tachionok meglepetésszerű létrejöttének az oka az éter elutasításához, a megértés kudarcához kötődik, vagy ahhoz, hogy megpróbálják megérteni a tehetetlenség fizikai mechanizmusát - és indul a matematikusok ámokfutása!

Az igazat megvallva, a legtöbb valódi fizikus nem hiszi el, hogy a tachionok valóban léteznek. A tachionok nem mások, mint a modern fizika sci-fi világa, és így természetesen a ténylegesen sci-fikben léteznek is. Nos, ez az az ötlet meg is érdemli, hogy szilárdan a sci-fi birodalmában maradjon.

Úgy gondolják, hogy a tachionok egy képzeletbeli tömegmező kvantumjai. Még az iránt is van erőfeszítés, hogy megpróbálják bemutatni, hogy létezik ilyen terület. Mivel a mainstream fizikusok úgy döntöttek, hogy figyelmen kívül hagyják azokat a tömegmodelleket, ahol a tömeg a nullponti energia tulajdonságú, még mindig menekülnek a téma elől. A képzeletbeli tömegmezők léte így egyszerűen hazugság a tachion-hazugságon belül.

A tachionok létezése hazugság. A fizika jobban járna, ha ezeket a hipotetikus elképzeléseket, beleértve a képzeletbeli tömegmezőt is, elvetnék.

90. hazugság: A fennmaradó hipotetikus részecskék

A fizikában a legnagyobb hazugságok 90. része a fennmaradó hipotetikus részecskék. Ahelyett, hogy az összes hipotetikus részecskét egyenként végignéznénk, sokkal egyszerűbb egyszerre elvetni az összest. Több tucat hipotetikus részecske kapcsolódik különféle elméletekhez. Sajnos van bennük egy közös elem: túlbonyolítják a részecskerendszert, amely már túlságosan bonyolult ahhoz, hogy alapvetően valóságos legyen.

Ezeknek a részecskéknek egy széles csoportja van, amely része az elektron-neutrínó kapcsolaton alapuló szuperszimmetria-hipotézisnek. Így a fizikusok előálltak a photinóval, a neutralinóval, a gluinóval, a gravitinóval, a higgsinóval és még sok mással. A szuperszimmetria úgy általában az egész hazugság. Létezik még a sötét foton, a sötét erő feltételezett hordozója. Vannak axionok, WIMPS-ek (gyengén kölcsönható masszív részecskék) és más részecskék, amelyekre szükség van az elméletekkel kapcsolatos problémák megoldásához, ha ezek az elméletek már kezdetben teljesen tévesek is.

Ez nem azt jelenti, hogy befejeztük a rezonanciák keresését. A Sternglass-modell sokkal több rezonancia előrejelzéséhez vezet, különösen, ha rezonáns proton-antiproton párokat kezdünk vizsgálni. A semleges pionnak megfelelő proton-antiproton pár rezonanciaállapota közel 250 GeV/c 2 lesz. A mezonokhoz hasonlóan számos más rezonanciaállapot is léteznie kell, amelyek proton-antiproton párok, elektron-pozitron párok, valamint egyedi elektronok, pozitronok, protonok és antiprotonok kombinációiból állnak.

Amint arra a 79. hazugság rámutatott, a fizika alapvető elméletéhez csak két alapvető részecske kell, az elektron és a proton, valamint ezek antianyag ellentétei. A fennmaradó kimutatható részecskék rezonanciák, a fennmaradó hipotetikus részecskék pedig hazugságok.

91. hazugság: G egy alapvető állandó

Dilbert: És tudjuk, hogy a tömeg hozza létre a gravitációt, mert a sűrűbb bolygóknak nagyobb a gravitációja.

Dogbert: Honnan tudjuk, hogy mely bolygók sűrűbbek?

Dilbert: Több a gravitációjuk.

Dogbert: Ez egy körkörös érvelés.

Dilbert: Inkább úgy gondolom, hogy nincs könnyű megoldás. 114

Scott Adams, 1999

A fizika legnagyobb hazugságai közül a 91. G egy alapvető állandó. G a newtoni gravitációból származó gravitációs állandó a 91-1 egyenlet szerint. A 26. hazugságból felidézhetjük, hogy a gravitáció nem alapvető erő, mert ez egy összetett erő két vagy három komponensből, kezdve azzal, hogy a nagyenergiájú gravitáció egymáshoz nyomja a tárgyakat, és a sötét erő löki szét őket.

91-1 egyenlet

Ezenkívül mechanikus Lorentz-típusú erők hatnak a testekre, amelyek érintőleges sebessége a keringő tömegközéppont felé tolja őket. A párhuzamos pályákon mozgó testek is egymáshoz nyomódnak, mint ahogy két párhuzamos áramú, párhuzamos vezeték is egymáshoz vonzódnak, de mechanikai erők hatására. A test forgása a mechanikai erő egy újabb összetevőjét vezeti be, ami sok más jelenséghez vezet.

A Newton-féle gravitációs állandó G hasonlóképpen két vagy három állandó szorzata, bár úgy tűnik, hogy a nagyenergiájú gravitáción kívül az összes erő egyetlen mechanikai erővé kombinálható. Még a nagyenergiájú gravitáció is egy kombinált elektromágneses és mechanikai erő összetevőjének tekinthető.

Nyilvánvaló, hogy a két vagy több különböző állandóból származó állandó nem alapvető állandó. Lehetséges, hogy a G gravitációs állandó alapvetőbb erőelvekből származtatható. Ha belevesszük, hogy a bolygók keringési mozgása a mechanikus Lorentz-erő hatására megváltoztatja G valós nagyságát, akkor ez nem igazán állandó.

Lehet, hogy azt gondolja, hogy úgy néz ki, mintha állandó lenne, amikor az egyes bolygókra vonatkozó pályaszámítást végezzük, de ez figyelmen kívül hagyja azt a tényt, hogy a tömeg szabad paraméter. Mivel a bolygó tömegét nem tudjuk megmérni a gravitációs számításoktól függetlenül, egyszerűen módosítjuk az egyes bolygók tömegértékét, hogy G állandó maradjon.

Ez a hatás sokkal észrevehetőbb a spirálgalaxisokban, ahol nincs elég tömeg a galaxisban ahhoz, hogy a spirálokat a newtoni gravitáció segítségével megmagyarázzák. A nagyobb tömeg azonban továbbra sem magyarázza meg a spirálokat.

Amikor a csillagok több mint százezer kilométer/másodperces sebességgel keringenek a galaktikus központ körül, nagyon erős mechanikus Lorentz típusú erő nyomja őket befelé, a galaktikus mag felé. Mivel két vagy több párhuzamos pályán lévő csillagot is összenyom a mechanikai erő, ezek is sávokat alkotnak. E további erők nélkül a spirálgalaxis legkülső csillagai az intergalaktikus térbe repülnének. Kompozit „állandóként” G más és sokkal nagyobb nagyságot vesz fel, ha nagy mechanikai Lorentz-erőket adunk hozzá. Kiderült, hogy még G-t konstansnak nevezni is hazugság. Az az állítás, hogy G alapvető állandó, hazugság.

G nem is állandó. A fizikusok manipulálják az objektumok tömegét, és kitalált sötét anyagot vezetnek be, hogy megpróbálják állandóvá tenni G-t, de ezek a javítások nem működnek, mivel további erőkre van szükség a sötét erő és a spirálgalaxisok szerkezetének magyarázatához.

114 S. Adams, Dilbert rajzsorozat, 1999. március 1.

92. hazugság: A gravitációs képlet fordított négyzetes törvénye

A fizikában a 92. legnagyobb hazugság a gravitációs képlet inverz négyzettörvénye. Visszatekintve az utolsó fejezetre, a 91-1 egyenlet nevezőjében egy r2 -t látunk. Ez azt jelenti, hogy a gravitációs erőnek a sugár négyzetével arányosan kell csökkennie, amit gyakrabban a távolság négyzetének neveznek. Ez a fordított négyzettörvény.

A fordított négyzettörvény egyben az energia-megmaradás elvének kijelentése is. Ha figyelembe vesszük az erő kiindulási pontjától eltérő távolságra lévő több gömb teljes felületére kiterjedő energiát, akkor az egyes gömbök energiája azonos. Ez azt jelenti, hogy az energia nem vész el. Ha az energia elveszne anélkül, hogy valódi fizikai mechanizmus elnyelné, az energia-megmaradás elvének megsértését vonná maga után.

Könnyen belátható, hogy ez hogyan sodor bennünket bajba. Az inverz négyzettörvény jól működik a Naprendszerünkben, ami természetesen Newton gravitációs elméletének bizonyítéka. Azonban ez nem működik olyan jól, ha a spirál-galaxisok vonatkozásában. Az utolsó fejezetben leírtak szerint nincs elegendő tömeg ahhoz, hogy Newton gravitációs elmélete megmagyarázza a legkülső csillagok vonzerejét. Az is bosszantó probléma, hogy nem magyarázza meg a spirálsávokat.

A dolgok furcsábbá válnak, ha külön galaxisokat nézünk. Ahelyett, hogy az összes galaxis összetömörülne, ahogy ezt egyedül a gravitációtól várnánk el, a legtöbb, de nem mindegyik, eltávolodik egymástól. A gravitáció nem tudja összetartani a dolgokat, amikor intergalaktikus távolságokat nézünk. A probléma leküzdésére a fizikusok azzal az ötlettel álltak elő, hogy volt egy robbanás, amely végül megadja a galaxisok sebességét, és tágulást okoz. Mivel a sötét erő magyarázza a gyorsulást, inkább úgy tűnik, hogy a nagyenergiájú gravitáció a távolsággal gyengül, vagy a sötét erő erősödik.

A döntő ebben az esetben az, hogy a tágulás üteme gyorsul, így tudjuk, hogy a sötét erő erősebb, mint a nagyenergiájú gravitáció intergalaktikus távolságokban. Azt is közlik velünk, hogy az egész tágulás a sötét erőnek köszönhető, nem pedig valamiféle visszamaradó sebességnek, ami egy réges-régi robbanásos eseményből származik.

Ezzel két lehetőséghez jutunk vissza, vagy a gravitáció gyengül a távolsággal, vagy a sötét erő erősödik, és mivel a sötét erő erősödése sértené az energia-megmaradás elvét, a gravitációnak gyengülnie kell valamilyen energiaelnyelő mechanizmus révén.

A gravitáció gyengeségének az oka, hogy van der Waals erők közvetítik: a dipólusok más dipólusokkal kölcsönhatásba lépve nyomóerőt hoznak létre. A gravitáció annak köszönhető, hogy az anyagtestek megzavarják ezeknek a van der Waals-erőknek az átvitelét, és árnyékhatást keltenek, csökkentve a testek közötti vákuumnyomást. Az anyag azonban nem csak nagy testekben létezik, hanem az egész univerzumban, egyébként üres térben terjed. Mindenhol vannak intergalaktikus részecskék, gáz, plazma és por. Ez azt jelenti, hogy a van der Waals erők a teljes útjuk mentén, minden test körül minden irányból megszakadnak. Végül a van der Waals erők olyan gyengék lesznek, minden oldalról, így nem számít, hogy egy csillag vagy galaxis van messze tőle. Ez az oka annak, hogy a becsült 1053 kilogramm tömeg a látható univerzumban nem okoz fekete lyukat.

A sötét erő viszont összhangban van a mechanikai erőelmélettel. Ez az azonos típusú töltésű testek közötti taszító erő. A sötét erőt a vákuum-dipólusok polarizációja továbbítja, egy olyan mechanizmus, amely nincs kitéve az intergalaktikus gázok és porok interferenciájának.

A gravitáció fordított négyzetes törvénye hazugság. A tudományos bizonyítékok alapján a gravitáció gyorsabban csökken, mint a távolság négyzete az intergalaktikus távolságokban.

93. hazugság: Degenerációs nyomás

A fizikában a 93. legnagyobb hazugság a degenerációs nyomás. A degenerációs nyomásról úgy gondolják, hogy a részecskék, különösen a Fermionok között kialakuló nyomási erő a Pauli-féle kizárási elv miatt. A Pauli-kizárási elv keretein belül két Fermion-részecske nem rendelkezhet egyidejűleg azonos kvantumállapottal.

Ennek a szabályalapú rendszernek azután feltehetően taszító nyomóerőt kell létrehoznia, mivel az azonos kvantumállapotú részecskék valahogyan lökdösik egymást, hogy ne sértsék meg a szabályt. Nem világos, hogy a részecskék hogyan „tudják”, hogy nem sértik meg a szabályt? Ez egy feltételezett erő, amely nem szerepel az alapvető erők szabványos modell-listájában.

Amint azt az előző fejezetekben tárgyaltuk, számos olyan rövid hatótávolságú taszító erő létezik, amelyeket a fizika standard modellje nem megfelelően számol. A következők között vannak taszító erők:

1. elektronok és protonok,

2. elektronok,

3. protonok,

4. protonok és neutronok,

5. neutronok.

A fenti listából láthatjuk, hogy az univerzum stabil anyagát alkotó három részecske mindegyikét taszítja mindhárom típusú részecske, a neutron-elektron kapcsolat kivételével. Ennek ellenére, ha még nem észlelték, megjósolom, hogy az elektronok és a neutronok közötti közeli tartományban olyan taszító erő van, amely hasonló a protonok és elektronok közötti erőhöz.

Visszatérve a degenerációs nyomás fogalmához, az első degenerációs erő az elektron-degenerációs erő, amelyről azt mondják, hogy nyomást okoz az elektronok között. Az 1920-as évek közepén és végén a fizikusok megpróbálták leírni a fehér törpecsillagok fizikáját. Ennek érdekében a Fermi-Dirac statisztikák alapján gázként modellezték őket. Ez a Fermi-gáz meglehetősen jól tükrözte a fehér törpék sűrűségét.

1931-ben Subrahmanyan Chandrasekhar alkalmazta ezt az elvet, és meg tudta határozni a fehér törpe csillag tömegének felső határát, amelyet Chandrasekhar-határként ismertek. 115 116 Chandrasekhar később Nobel-díjat kapott munkájáért, William Fowlerrel együtt. Hipotézise keretein belül a Chandrasekhar határérték felett a gravitáció elég erős ahhoz, hogy legyőzze az elektrondegenerációs nyomást, és a fehér törpe neutroncsillaggá omlik össze.

Ha visszatekintünk a taszító erők listájára, könnyen beláthatjuk, melyik szab határt a neutronképződésnek. Ez a protonok és elektronok közötti ~780 keV taszítóerő. Amint a gravitáció elég erős lesz ahhoz, hogy legyőzze ezt a taszító erőt, vagy legalábbis elég közel kerül ahhoz, hogy a gyenge kölcsönhatások a normálisnál sokkal nagyobb sebességgel termeljenek neutronokat, a fehér törpe neutroncsillaggá omlik össze. A Chandrasekhar határ hazugság, legalábbis a hipotézisét illetően. A tényleges határ valós, de ez az elektronok és protonok közötti taszító erőnek köszönhető.

Egy általánosabb témában Freeman Dyson nevéhez fűződik annak megállapítása, hogy az anyag szilárdsága az elektronok degenerációs nyomásának köszönhető. 117 118 119 Régóta felteszik a kérdést, hogy miért érzi magát szilárdnak az anyag, amikor többnyire üres tér. Mivel a fizikusok figyelmen kívül hagyták a részecskék közötti különböző taszító erőket, általában az anyag szilárdságát elektromágneses erőknek tulajdonították. Dyson kimutatta, hogy ennek az elektron-degenerációs nyomásjelenségnek több értelme van.

Bizonyos értelemben Dysonnak igaza van, ebben az anyagban szilárdnak érzi magát az elektronok közötti taszító erő miatt. Az a tévedése, hogy ez az erő nem valamiféle nyomóerőnek köszönhető, amely a Pauli-féle kizárási elv következtében keletkezik. Az elektronok nem „ismerik” a szabályt; valódi erő felelős érte. Az anyagot szilárdnak érzi az elektronok közötti taszító erő, az elektronok közötti taszító erőt pedig egy alapvető erő. Dyson hipotézise az anyag szilárdságáról hazugság.

A Chandrasekhar határérték helyes értékének megállapítása érdekében a fizikusoknak korrekciót kellett hozzáadniuk a protondegeneráció figyelembevételéhez, mivel a Pauli-féle kizárási elv szerint a protonokra más protonokhoz hasonló nyomást kell gyakorolni. A protondegenerációnak ezt a koncepcióját feltételezték az erős erő taszító összetevőjének okaként.

A valóságban a protonok sem „tudják”, hogy létezik egy szabály. Természetesen van taszító erő a protonok között, de ennek semmi köze Pauli kizárási elvéhez, mivel ez egy igazi erő. Ezt azért tudjuk, mert a protonok és a neutronok között taszító erő van, amit a Pauli-féle kizárási elv nem jósol meg, mivel két különböző típusú részecskéről van szó.

A fizikusok ekkor felismerték, hogy nyilvánvalóan léteznie kell neutron-degenerációnak is. Eszerint a neutronok között nyomáserőnek kell lennie, amelyet Pauli kizárási elve okoz, és ez a hipotetikus erő az, amely megakadályozza a neutroncsillagok összeomlását, legalábbis addig, amíg tömegesebbé nem válnak. A proton-degenerációhoz hasonlóan a neutronok közötti taszító erő valódi erő, nem pedig Pauli kizárási elvének valamilyen terméke. A neutronok sem „ismerik” ezt a szabályt.

A szabályalapú elvek veszélyesek a fizikában, különösen akkor, ha részleges információn alapulnak. A Pauli-féle kizárási elvről már az 52. hazugságban is bebizonyosodott, hogy hazugság, azzal kapcsolatban, hogy miként használják új típusú kvantumszámok bevezetésére, amelyeknek nincs alapja a fizikai valóságban. Itt a Pauli-féle kizárási elv az erők magyarázatára szolgál, amikor nem alapvető erőről van szó. Az elektron-, proton- és neutron-degeneráció mind hazugság.

Vannak rokon kifejezések, amelyek szintén hazugságok, mivel a degenerációs nyomás alatt álló anyag a degenerált anyag nevet kapja. Ezt követően elektrondegenerált anyag van, mint például a fehér törpecsillagokban, és neutron degenerált anyag a neutroncsillagokban. Létezik a tisztán hipotetikus kvark degenerált anyag is, amelyről azt gondolják, hogy létezhet a fekete lyukakban, de valójában nem létezhet, mivel a kvarkok nem reálisak.

A degenerációs nyomás hazugság. Az anyagrészecskék között valódi taszító erő van, ami nem a Pauli-féle kizárási elvnek köszönhető.

115 S. Chandrasekhar, „The Density of White Dwarf Stars”, Philosophical Magazine, (7. sorozat), 11., 592–596., 1931.

116 S. Chandrasekhar, „The Maximum Mass of Ideal White Dwarfs”, Astrophysical Journal 74, 81–82, 1931.

117 F. J. Dyson, A. Lenard, "Stability of Matter I", J. Math. Phys. 8 (3): 423–434, 1967.

118 A. Lenard, F. J. Dyson, "Stability of Matter II", J. Math. Phys. 9 (5): 698–711, 1968.

119 F. J. Dyson, "Töltött részecskék véges rendszerének alapállapot-energiája", J. Math. Phys. 8 (8): 1538–1545, 1967.

94. hazugság: Neutroncsillag mérethatár

A fizikában a 94. legnagyobb hazugság a neutroncsillagok mérethatára. A neutroncsillagok mérethatárát általában Tolman–Oppenheimer–Volkoff (TOV) határértéknek nevezik, amely azt mondja ki, hogy egy neutron degenerált anyagból készült test méretének van határa. Ez analóg a fehér törpecsillagokra vonatkozó Chandrasekhar határértékkel, amely az elektron degenerált anyag határértékein alapult.

A TOV határérték, mint más degenerált anyagok esetében is, a Pauli-féle kizárási elv modelljén alapul. Úgy gondolták, hogy a degenerációs nyomás miatt van határa annak, hogy mekkora lehet egy neutroncsillag, ha megtámasztják. J. Robert Oppenheimer és George Volkoff dolgozta ki a határt Richard Chace Tolman által kifejlesztett módszerekkel. 120,121

Eredeti becslésük végül kisebb volt, mint a Chandrasekhar határértéke a fehér törpecsillagokra, amelyek 0,7-szerese a napunk tömegének. A TOV határértéket később átdolgozták, hogy belefoglalja a neutronok közötti taszító erőt is, amelyet hamisan az erős erőnek tulajdonítottak, hogy a becslést a nap tömegének körülbelül 1,5-szeresére emeljék. Így a TOV-korlát nagyobb lett, mint a Chandrasekhar ~1,4-es határa. Más, újabb becslések szerint a nap tömegének háromszorosa is lehet. A neutroncsillagokat az 1,4-2 naptömegű tartományban figyelték meg, az alsó oldalon némileg átfedve a fehér törpéket.

Abban az esetben, ha hiányzik a megoldás: a helyes érték kiszámítása érdekében a degenerációs nyomás helyett a neutronok közötti taszítóerőt kellett volna használniuk. Végső soron ez a neutronok közötti taszító erő, amely a neutroncsillagok megfelelő tömegéhez vezet, nem pedig a degenerációs nyomás. Még ha a degenerációs nyomás valós is lenne, a neutroncsillagok méretét meghatározó fontos erő a neutronok közötti taszító erő lenne, amely erő nem szerepel a standard modellben.

És képzeld csak el, hogy a neutronok taszítóerejének nincs ismert határa. Amennyire tudjuk, mind a modelljeink, mind a kísérleteink alapján nincs olyan pont, ahol a neutronok közötti taszító erő, vagy ugyanaz az erő a protonok között, vagy a protonok és a neutronok között megszűnne.

A kísérleti bizonyítékok nem azt mutatják, hogy a protonok ráhelyezhetők más protonokra. A bizonyítékok nem azt mutatják, hogy a protonok neutronokra helyezhetők, vagy fordítva. A bizonyítékok nem azt mutatják, hogy a neutronokat más neutronokra lehetne helyezni. Az atommagok nem véletlenszerűen esnek össze varázsütésre, ahogy azt a kvantumelméletből várnánk, ami abból lehetséges lenne.

Valahogy a fizikusok figyelmen kívül hagyják a tényeket, mert azt akarják hinni, hogy a részecskéket tovább lehet tömöríteni. Kvantumvilágban élünk, és ha léteztek volna ilyen egymásra épülő állapotok, láttuk volna őket, ha csak ritkán is. Statisztikailag a proton bomlásához hasonlítható. Ha valaha is előfordult volna a világegyetem történetében, már a laboratóriumban láttuk volna.

Van még egy módja annak, hogy megvizsgáljuk a problémát. Tekinthetjük a gömbön belüli gravitációs erőt, mivel ez a fekete lyukon belüli anyagra ható gravitációs erőkről árulkodik közvetlenül a keletkezése után. Amit fontos tudni, hogy egy gömb alakú anyagból és energiából álló héjon belül, a héjnak köszönhetően a gravitációs erő a héjon belül mindenhol nulla.

Ez azt jelenti, hogy a nagyobb sugarú anyag gravitációs hatással nincs a sugáron belüli anyagra. Következésképpen egy fekete lyuk kialakulása után nem hat új gravitációs erő a benne lévő anyagra. Nincs új anyag vagy energia, mely ránehezedik a neutroncsillagra, miután fekete lyukká válik, mivel minden anyag és energia örökre megreked az eseményhorizonton.

A neutroncsillagok nem omlanak össze más sűrűbb anyaggá. Nincs olyan sűrűbb anyag, amelybe összeeshetne. A neutronokra nincs extra gravitációs erő. A fekete lyukban lévő neutroncsillagokra nincs további nyomás. Nincs ismert kvantummechanizmus a neutronok közötti taszító erő leküzdésére, még akkor sem, ha volt erő, amely ezt kiváltotta volna.

A neutroncsillagok egyszerűen tovább nőnek, amíg fekete lyukká nem válnak, majd megállnak, ahogy az anyag és az energia felhalmozódik az eseményhorizonton.

A neutroncsillagok mérethatára (TOV limit) hazugság. Nincs ismert erő, amely korlátozná a neutroncsillagok tömegét, és nincs bizonyíték arra, hogy két neutron létezhet egymásra épülő állapotban.

120 R.C. Tolman, "Static Solutions of Einstein's Field Equations for Spheres of Fluid." Physical Review, 55 (4): 364–373, 1939.

121 J.R. Oppenheimer, G.M. Volkoff, "On Massive Neutron Cores". Physical Review, 55 (4): 374–381, 1939.

95. hazugság: Relativisztikus fekete lyukak

A fizika legnagyobb hazugságai közül a 95. a relativisztikus fekete lyukak. A fekete lyuk fizikája nagy figyelmet kap a népszerű tudományos és tudományos-fantasztikus irodalomban. A művészek lenyűgöző képeket terveztek, hogy felébresszék az emberek fantáziáját és csodálkozást okozzanak. A fizikus-szórakoztatók és az őket körülvevő emberek egy halom pénzt keresnek a fekete lyukakból.

John Michell 1783-ban fedezte fel először a fekete lyukakat, vagy ahogy ő nevezte őket, fekete csillagoknak. 122 A fény korpuszkuláris elmélete alapján tisztán klasszikus perspektívából tudta megjósolni a fekete csillagokat. Az az elképzelés, hogy a fény diszkrét csomagokban vagy kvantumokban utazik, nem volt igazán új 1905-ben, csak Planck elméletének köszönhetően javult. Michell meg tudta jósolni, hogy számos fekete csillag létezik.

Az 1900-as években Karl Schwarzschild volt az első, aki pontos megoldást talált Einstein 1915-ösáltalános relativitáselméletének egyenleteire, ahol úgy írta le a fizikát, amely később a relativisztikus fekete lyuk elmélethez vezetett. 123 De csak jóval később John Archibald Wheeler alkotta meg a „fekete lyuk” kifejezést.

Michell elképzeléseiből és Schwarzschild-egyenleteiből kiindulva azt találjuk, hogy létezhet olyan ultrasűrű test, ahol semmi, még a fény sem menekülhet el gravitációs erejétől, legalábbis nem klasszikus módon. Egy ilyen test sugarának egyenlete, amelyet Schwarzschild-sugárnak neveznek, a 95-1 egyenlet mutatja.

95-1 egyenlet

Fontos megjegyezni, hogy amint azt John Michell megmutatta, ez az egyenlet tisztán klasszikus módon is levezethető anélkül, hogy Einstein általános relativitáselméletének hókuszpókuszához folyamodnánk.

Vegye figyelembe itt a „konstans” G-t is, amely valójában nem állandó, és a másik nem annyira alapvető állandó, a fénysebesség is benne van foglalva az egyenletben. Mind a G, mind a c „állandót” alapvetően a vákuum-ingadozások tulajdonságaiként írják le. Ez azt jelenti, hogy újra meg kell vizsgálnunk őket a fekete lyukak összefüggésében, de ezt itt nem tesszük meg.

Noha egy ilyen ultrasűrű objektum körüli gravitációs erő vitathatatlanul nagy, nincs görbült téridő. A görbült téridő egy másik hazugság. A fekete lyukban és körülötte lévő tér geometriailag még mindig lapos - ennyit a képzeletbeli teóriáról.

A fekete lyukak ultrasűrű előfutárai a neutroncsillagok, amelyekről az előző fejezetben volt szó. A neutroncsillagok akkor jönnek létre, ha a gravitációs energia elegendő a protonok és elektronok közötti erő leküzdéséhez. Ezeket a neutronokat az erős nukleáris erő, az erős Casimir-erő nyomja egymáshoz, míg a neutronok között kb. 0,7 x 10-15 méteres távolságban meg nem indul az erős erővel ellentétes erő.

A fizikusok azt feltételezik, hogy a neutroncsillagok gravitációs hatására összeomlanak, amikor elérik a két és három naptömeg közötti tömeget. Az utolsó fejezetben felvázolt okok miatt a nagy neutroncsillagok összeomlása hazugság. Ha elég nagyok, a neutroncsillagok klasszikus fekete lyukakká válnak. A relativisztikus fekete lyukak gravitációs összeomlása nem bizonyított és szükségtelen. És ha egy fekete lyukban vagyunk, ahogy az alapelmélet sugallja, akkor tudjuk, hogy a fekete lyuk belsejének relativisztikus elmélete téves.

Azt is fontos megjegyezni, hogy egy fotonnak örökre szüksége lenne az eseményhorizont elhagyására. És szinte végtelen vöröseltolódása lenne, és észrevehetetlen lenne. A klasszikus fekete lyuk továbbra is fekete lenne, mivel egyetlen foton sem kerülheti el az eseményhorizontot.

A fénysebesség határértéke azt jelenti, hogy a standard modellen belül a gravitáció megszűnne létezni az eseményhorizontnál, mivel a gravitonok vagy bármi más nem haladhatja meg a fénysebességet. Jó dolognak tekinthetjük, hogy a gravitáció a fénysebességnél gyorsabban terjed. Ha nem, a gravitáció nem lenne észlelhető a fekete lyuk eseményhorizontján kívül. Szerencsére a vákuum ingadozásának csak kis mértékben kell forognia ahhoz, hogy az erőket átadjanak, még ilyen szélsőséges körülmények között is.

A gravitációs tömeg olyan, mint a relativisztikus tömeg, nem korlátozódik a nyugalmi tömegre. Tehát az effektív tömeg a végtelenbe megy az eseményhorizontnál, miközben az órajelek nulla felé közelítenek. Tehát amint egy klasszikus fekete lyuk kialakul, az eseményhorizontján nagy sűrűségű energiájú héjat kezd kialakítani. A klasszikus fekete lyuk ekkor egyfajta fekete gömbbé válik.

A relativisztikus fekete lyuk hipotézis egy másik nem tudományos vallási hipotézis, amely a fizikát a következőképpen fertőzte meg:

1. Nincs rájuk tárgyi bizonyíték.

2. A relativisztikus modell szükségtelen a fekete lyukak leírásához.

3. A relativisztikus modell szükségtelen bonyodalmakat ad a fekete lyukak elméletéhez.

4. Egy relativisztikus fekete lyuk összeomlott belsejét soha nem lehet kimutatni.

A relativisztikus fekete lyuk modell hazugság.

Itt az ideje, hogy más megközelítést alkalmazzunk a fekete lyukak tudományához, és abbahagyjuk a szenzációhajhász sci-fi propaganda terjesztését.

122 J. Michell, "Az állócsillagok távolságának, magnitúdójának stb. felfedezésének eszközeiről...", Philosophical Transactions of the Royal Society of London, The Royal Society, 74: 35–57 & Tab III, 1784.

123 K. Schwarzschild, "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. 7: 189–19, 1916.

96. hazugság: Hawking-sugárzás

A fizika legnagyobb hazugságai közül a 96. a Hawking-sugárzás. Stephen Hawking javasolta ezt a fekete lyuk sugárzási hipotézist, amely az ő nevét viseli. 124 Az alapkoncepció megköveteli a vákuum-ingadozást, ami akkoriban meglepő volt, hiszen a fizika területén az éterelutasítók uralták. Valamilyen ismeretlen okból azonban ebben az esetben engedélyezték, miközben a fizika legtöbb más területén figyelmen kívül hagyták.

Az alapötlet nála az, hogy amikor egy vákuum-fluktuációs részecskepár jön létre közvetlenül a fekete lyuk eseményhorizontján kívül, akkor bizonyos esetekben egy részecskepár egyik részecskéje átlépi az eseményhorizontot. Amint a vákuum ingadozása átlépi az eseményhorizontot, nem léphet vissza. Hawking elképzelése az volt, hogy bizonyos esetekben a másik részecske szabadon marad az eseményhorizonton kívül, és mivel ezeket a párokat fotonoknak tekintette, ennek a szabad fotonnak volt esélye arra, hogy fénysebességgel utazva elkerülje a fekete lyuk gravitációs vonzerejét.

A kiszabaduló vákuumfluktuációs foton energiát visz el, és mivel Hawking úgy gondolta, hogy az energiának máshonnan kell származnia, mint a nullapontos mezőből, az energiának a fekete lyukból kellett származnia. Ily módon a fekete lyuk energiát sugározhat ki. Az évek során, ahogy a kvantumhatásokat a fekete lyuk eseményhorizontjában tovább vizsgálták, felmerült a kérdés, hogy egy foton valóban el tud-e menekülni. A fekete lyukak valójában nem sugározhatnak.

A Hawking-sugárzási hipotézis problémája ennél is rosszabb. Amint azt az 5. és 6. hazugságban tárgyaltuk, virtuális fotonok nem léteznek, következésképpen az éter nem virtuális fotonokból áll. Ehelyett az éter elektron-pozitron és proton-antiproton részecskepárokból áll. A Hawking-sugárzási hipotézis újragondolása töltéssel és tömeggel rendelkező részecskékkel megváltoztatja a dolgokat. A masszív részecskék nem fénysebességgel, de legjobb esetben is valamivel kisebb sebességgel haladnak.

Következésképpen az az egész elképzelés, hogy az újonnan felszabaduló elektron vagy proton megszökik egy fekete lyuk gravitációs vonzása elől az eseményhorizonton kívülről, értelmetlen. Ha egy virtuális elektron-pozitron pár keletkezik közvetlenül az eseményhorizonton kívül, és az egyik beesik, akkor csak rövid idő kérdése, hogy a másik is beessen. Természetesen egy másik probléma, hogy az idő, ameddig egy részecske beesik, örökre szól, így ez soha nem történik meg. Egy részecske valójában soha nem lépi át az eseményhorizontot.

Ha egy pillanatra figyelmen kívül hagyjuk az örök problémát, a két részecske kereszteződhet egy másik részecskepárral. Ritka esetekben elképzelhetünk két elektron-pozitron párt egymás mellett úgy, hogy az egyik elektronpár és a másik pár pozitronja találkozik az eseményhorizonton, és megsemmisül. Ez egy elektront és pozitront kissé az eseményhorizonton kívül hagy. Ha ez a pár megsemmisül, mielőtt túllépné a Planck és Heisenberg határértékeket, akkor energiája visszatér a vákuumba.

Ha valahogy túl sokáig léteznek, akkor tömeggel rendelkező szabad részecskékké válnak, és energiát vesznek fel a fekete lyukból, a nullponti mezőből vagy máshonnan. Nem igazán tudjuk, hogy melyik. Aztán ha sikerül valahogy megsemmisíteniük egymást, mielőtt az eseményhorizontnál ragadnának, fotont termelnének. Ennek a fotonnak viszont van esélye elmenekülni, de ez csaknem végtelen ideig tartana, és szinte végtelenül lefelé tolódott volna el lényegében nulla energiára, tehát lényegében semmiféle energia nem tudna kiszabadulni.

A Hawking-sugárzás hazugság. A fekete lyukak nem sugároznak ki energiát úgy, hogy egy virtuális fotonpár a felét elnyeli.

124 S. Hawking: „Fekete lyuk robbanások?” Nature 248, 30, 1974.

97. hazugság: Szingularitások

A fizikában a 97. legnagyobb hazugság a szingularitás. Úgy gondolják, hogy a szingularitások a standard modellben akkor fordulnak elő, amikor egy test összeomlik, amikor tömege rendkívül nagy lesz. A fizikusok úgy vélik, hogy amint a neutronok degenerációs nyomásának határát (Hazugság #94) elérjük, minden anyag összeomlik, először kvarkanyag degenerálódik, majd szingularitás alakul ki. Ezen a ponton lényegében az összes energia egy dimenzió nélküli pontba tömörül. Ezeket néha gravitációs szingularitásoknak vagy tér-idő szingularitásoknak is nevezik.

A leggyakrabban tárgyalt szingularitások egy relativisztikus fekete lyuk közepén (95. hazugság) vagy az ősrobbanás elején (34. hazugság) találhatók. De szingularitások állítólag minden testben előfordulnak, amely képes legyőzni a degenerációs nyomás minden formáját (93. hazugság). A szingularitások gyakran előfordulnak görbült tértételek alkotásaiként (43. hazugság), különösen az általános relativitáselmélet keretein belül (44. hazugság).

Úgy tűnik, hogy kialakul egy minta. A szingularitások olyanok, mint a paradoxonok. Ha egy modell paradoxonokhoz vezet, akkor az a modell hazugság. Ha egy modellnek vannak szingularitásai, akkor az hazugság.

A szingularitások hazugságok. A részecskék közötti taszító erő megakadályozza az anyag összeomlását. A szingularitások sci-fi-k.

98. hazugság: Féreglyukak

A fizika legnagyobb hazugságai közül a 98. a féreglyukak. A féreglyukak, technikailag Einstein-Rosen hidak néven ismertek, az általános relativitáselmélet (44. hazugság) hipotetikus jellemzői, amelyekről úgy gondolják, hogy két pontot kapcsolnak össze a téridőben. Úgy gondolják, hogy a féreglyukak a fénynél gyorsabb utazást tesznek lehetővé (88. hazugság) hatalmas távolságokon az űrben, és mint ilyenek, nagyon népszerűek a sci-fi rajongók és a rajtuk pénzt kereső emberek körében.

A féreglyuk ötlet egy relativisztikus fekete lyukkal kezdődik (Lie #95), amely beengedi az anyagot, de nem engedi ki. A fekete lyuk egyenletek kiterjesztésével elképzelhető egy hipotetikus fehér lyuk, amely csak az anyagot engedi be. Ez egy olyan eset, amikor a matematikusok ismét tudományos-fantasztikus dolgukat végzik.

Aztán ha valamilyen módon egy fekete lyuk és ez a mitikus fehér lyuk összekapcsolódik a téridőn keresztül, akkor feltehető vagy pontosabban fantázia szerint, hogy valaki utazhat az egyik végén be, és a másik végén ki, mindaddig, amíg nem ütközik szingularitásba ( Hazugság #97). A fehér lyuk egy másik tér- és időpontba lökné ki őket. A matematikai fizikusok ezután eljátszottak a matematikával, hogy megtalálják a módját, hogyan tegyék stabillá őket, és lehetővé tegyék a kétirányú utazást.

Noha a féreglyukakról jó ötlet lehet fantáziálni, szilárdan csak a fantasyland és a science fiction világában léteznek. Az általános relativitáselmélet, amelyen az elképzelés alapul, hazugság, a relativisztikus fekete lyukak léte hazugság, a szingularitások léte hazugság, és igen, a fehér lyukak léte is hazugság.

A féreglyukak léte tehát hazugság. Nem más, mint egy rossz elmélet matematikai fabrikációja. A sci-fi birodalmában kell maradniuk, és nem szabad összetéveszteni őket a valós fizikával.

99. hazugság: Az anyagtermelés sérti az energiatakarékosság elvét

A fizikában a 99. legnagyobb hazugság az, hogy az anyagtermelés sérti az energiamegmaradás elvét. A fizika talán legnagyobb hátralévő kérdései az anyagtermeléssel kapcsolatosak.

a. Honnan jön az anyag?

b. Mi az energia forrása?

c. Hogyan keletkezik az anyag?

d. Hogy csak anyag van és nem antianyag?

A legnépszerűbb válasz ezekre a kérdésekre az ősrobbanás modell (Lie #34), de az ősrobbanás valójában nem oldja meg ezeket a problémákat.

Ami az energia-megmaradás elvét illeti, kimondja, hogy energiát nem lehet létrehozni vagy elpusztítani. Az energia azonban átalakítható egyik formából a másikba, beleértve a tömeget is. A hasadás, a fúzió, az akkumulátorok és a szénhidrogén-üzemanyagok használata mind példák az egyik energiaforma másikká alakítására. Energiát, beleértve az anyagot is, nem lehet előállítani a semmiből.

Ismét itt van egy probléma, amit az éterelutasítók okoznak. Azt gondolták, hogy a tér üres, teljes vákuum, éter nélkül. Tehát az anyag természetesen nem származhat ilyen üres térből. De egy lépéssel tovább lépnek a dolgokon, és kitalálják a nem-űr ötletét (28-as hazugság), amivé egy ősrobbanás is kinőhet, és ez valahogy rendben is lenne. De egyáltalán nincs rendben. A nem-térből előállított anyag hazugság. Ez valóban megsértené az energia-megmaradás elvét.

Azt mondhatjuk, hogy mivel az anyag létezik, tudjuk, hogy az anyag valamilyen módon keletkezik. Nem varázsütésre jelent meg. És az űr tele van vákuumenergiával, sokkal jobban, mint amennyi szükséges ahhoz, hogy a látható világegyetem összes tömegenergiáját figyelembe lehessen venni. De itt az étert elutasítók azt mondják, hogy a vákuumenergia nem számít. Nem veszik figyelembe a vákuumenergiát az energia-megmaradás elvével kapcsolatos gondolkodásukban. Számukra a vákuumenergiából származó energia is az elv megsértését jelenti.

Ha azt mondjuk, hogy az energia nem energia, az energia-megmaradás elvének megfelelően egy másik hazugság. Az energia energia, és az egyik forma átalakulhat egy másikká, ha van olyan fizikai mechanizmus, amely lehetővé teszi, hogy ez megtörténjen. Egyes fizikusok a vákuumenergiát „negatív energiának” nevezték, de ez egy újabb hazugság.

Mint minden energiaforma, a vákuumenergia is pozitív energia. A negatív energia önmagában egy újabb hazugság. Kiderült, hogy könnyen belátható az, hogy hogyan származhatnak elektronok, protonok és neutronok a vákuumenergiából. A vákuumot virtuális elektron-pozitron és proton-antiproton dipólusok töltik ki, így tudjuk, hogy ezek a részecskék már ott vannak, melyek szigorúan az anyagrészecskék kijuttatásáról szólnak, elkülönítve az antianyag részecskéktől. Ha már rendelkezünk elektronokkal és protonokkal, ezek egyesülve neutronokat képeznek.

Azt is megállapítottuk, hogy a proton, a neutron és az elektron tömege megegyezik az általuk kiszorított vákuumenergiával.

Az energia mennyisége egy adott térfogatban változatlan, függetlenül attól, hogy vannak-e benne részecskék, vagy sem. Akár módosíthatjuk is az energia-megmaradás elvére vonatkozó kijelentésünket, hogy kijelentsük: a tér egy régiójában a teljes energia állandó. Ez az energia minden formájára igaz; itt azonban nincs hely a részleteken végigmenni. Kérjük, olvassa el a dolgozatomat, az energia-megmaradás nullapontos energiáját magában foglaló elvét, amely összhangban van a világegyetem nulla nettó energiájával. 125

A részecskék nemcsak már jelen vannak, de amikor szabad részecskékké válnak, nem befolyásolják a tér teljes energiáját. A protonok, neutronok és elektronok vákuumenergiából történő előállítása nem sérti az energia-megmaradás elvét. Az az állítás, hogy a nullponti energiából nem állítható elő az anyag, hazugság.

Ez megválaszolja az a és b kérdéseket, így csak a c és a d marad. Sajnos ezekre ma nincs válaszom önöknek, bár vadul spekulálhatnék, mégis ellenállok ennek a kísértésnek.

Tudjuk, hogy van valamilyen mód az elektronok és protonok vákuumból való kinyerésére. A fizika talán legnagyobb problémája a hogyan kitalálása, és ennek ellenére aligha dolgozik rajta valaki. Legalábbis alig dolgozik ezen kísérletező fizikus, és itt kell megtörténnie az áttörésnek. Senki sem fog elhinni egy anyagtermelési hipotézist, amíg valaki nem tudja bizonyítani az anyagtermelést a laboratóriumban. Ez egy olyan kutatási terület, amely több figyelmet és finanszírozást érdemel. Ki kell tudnunk találni egy módot arra, hogy a Higgs-rezonanciák előállítása költségének töredékéért anyagot állítsunk elő.

Az az állítás, hogy az anyagtermelés sérti az energia-megmaradás elvét, hazugság. Tudjuk, hogy az anyagot elő kell állítani. Csak idő kérdése, hogy az anyag keletkezésének titka megfejtésre kerüljön.

125 R. Fleming: „A nullpont energiát magában foglaló energiamegmaradás elve, amely összhangban van a nulla nettó energiával az univerzumban.”

https://www.researchgate.net/publication/283795822_A_zero-point_energy_inclusive_principle_of_conservation_of_energy_consistent_with_zero_net_energy_in_the_universe

100. hazugság: Négy alapvető erő létezik

Minden bizonnyal egy olyan egyszerű, olyan szép gondolat áll mögötte, hogy ha megragadjuk – egy évtized, egy évszázad vagy egy évezred múlva – mindannyian azt mondjuk egymásnak, hogyan is lehetett volna másképp? 126

John Archibald Wheeler 1986

A fizikában a 100. legnagyobb hazugság az, hogy négy alapvető erő létezik. A fizika standard modelljében négy alapvető erőről beszélünk:

1. az elektromágneses erő,

2. a gravitációs erő,

3. a gyenge erő,

4. az erős erő.

A fizikusok megpróbálták leírni az összes erőkölcsönhatást ezzel a négy erővel, miközben megpróbálták egyesíteni őket. Az elektromos és a gyenge erőről azt mondják, hogy a gyenge kölcsönhatási modell alapján már egységes, ahol ezeket a kölcsönhatásokat a W és Z bozonok közvetítik. Tehát a standard modell valójában három erőt használ fel az egyesítéshez.

Ahogy végigmentünk a különféle hazugságokon, átfogóbb listát készítettünk az erőkről. Ezek:

1. mechanikai erő,

2. elektromágneses erő,

3. gyenge erő,

4. erős erő,

5. sötét erő,

6. nagy energiájú gravitációs erő,

7. taszító erő az elektronok és a protonok között,

8. taszító erő az elektronok között,

9. taszító erő a protonok között,

10. taszító erő a protonok és a neutronok között,

11. taszító erő a neutronok között,

12. vonzóerő az elektronok között.

Ehhez a listához hozzáadhatnánk a degenerációs nyomást (93. hazugság), a Pauli-elvű erőt, kivéve, hogy redundáns a 8-as, 9-es és 11-es számok, az elektronok, protonok és neutronok közötti taszító erők tekintetében. Feltételezhetjük azt is, hogy az elektronok és a neutronok között közeli hatótávolságú taszító erők lépnek fel, mivel a három elsődleges részecske összes többi részecskekombinációjáról ismert, hogy taszító erőt mutatnak.

A mechanikus erőktől kezdve világos, hogy ezek valódi erők, nem pszeudoerők, és valamilyen módon a végső listán kell szerepelniük. Később visszatérünk rájuk. Úgy tűnik, hogy az elektromágneses erők a legalapvetőbbek az összes erő közül, és mindenképpen a listán kell maradniuk.

A gravitációs erő nem alapvető erő, mivel három erő, a mechanikai erő, a sötét erő és a nagyenergiájú gravitációs erő összege. Ezért lemaradt a második listáról.

A nagy energiájú gravitációs erő Fatio-Casimir erőnek tűnik. A Casimir-erő léte azt sugallja, hogy léteznek vákuum-ingadozások, és ezek az anyagot vonzák. Azt is elmondja nekünk, hogy az anyag rugalmatlanul viselkedik ezzel a nyomóerővel szemben, ahogy azt Fatio elmélete megköveteli. Ezenkívül a Casimir-erő azt mondja nekünk, hogy a testek nem melegednek fel a vákuum-ingadozásokkal való kölcsönhatás miatt. Fatio elméletének minden fő hibája egyáltalán nem hiba. A Casimir-effektus megléte azt sugallja, hogy a Fatio-Casimir-effektusnak is léteznie kell. Ez azt jelenti, hogy a Fatio-Casimir nagyenergiájú gravitáció nem különálló erő, hanem elektromágneses és mechanikai hatás, és egy kombinált elektromechanikus erő része.

A gyenge erő, pontosabban a gyenge kölcsönhatások könnyen magyarázhatók elektromágneses erőként, de nem a szabványos modellben leírt módon. Az olyan gyenge kölcsönhatások, mint a nukleáris bomlás, könnyen megmagyarázhatók a részecskék és a virtuális részecskepárok közötti megsemmisülési és termelési eseményekkel. Amennyiben ez egy erő, az az elektromágneses elméleten belüli kvantumelektrodinamika része. Hazugság a gyenge erőt alapvető erőnek nevezni.

Következők az erős erők. Az erős erő szintén két erő kombinációja, egy erős vonzóerő és egy erős taszító erő. A taszító erők külön-külön vannak felsorolva a 9., 10. és 11. számban. Ami az erős vonzóerőt illeti, könnyen kimutatható, hogy ez a Casimir-erő, amely elektromágneses erő, és egyáltalán nem különálló erő. Hazugság az erős erőt alapvető erőnek nevezni.

A sötét erő az anyagtestek közötti hosszú távú taszító erő, amely a világegyetem gyorsuló tágulásáért felelős. A mechanikai erő magában foglalja a mechanikus dipólust, amely szinte biztosan anyag és antianyag. Mindenesetre a mechanikai erő megköveteli, hogy az anyagot eltaszítódjon az anyagtól. Még ha a dipólus valami más is lenne, az anyagtestek akkor is eltaszítódnak egymástól, amint az a 7-11. ábrán látható. A sötét erő tehát nem más, mint a mechanikai erő összetevője.

A 7-es, 8-as, 9-es, 10-es és 11-es részecskék közötti taszító erőket egyesíthetjük, mivel ezeknek összefüggésben kell lenniük. Úgy tűnik, ezek az erők az anyagrészecskék közötti alapvető taszító erő részét képezik. Ez ismét egy olyan dolog, ami összhangban van a mechanikai erővel.

Vegye figyelembe, hogy a mechanikai erő azt is megköveteli, hogy az anyagot vonzzák az antianyaghoz, így az elektronok a pozitronokhoz, a protonok az antiprotonokhoz stb. Mivel a részecskék antirészecskéikkel együtt megsemmisülnek, ennek az egy részének van értelme, mivel nem taszítják el egymástól kis távolságra. Megsemmisülést és részecskebomlást is látunk, amikor egy antiproton vagy pozitron kölcsönhatásba lép egy neutronnal, ami inkább vonzó erőt jelez, mint taszító erőt.

Így a pozitronok és a protonok között egy közeli vonzerőt hagyunk magunk mögött; mivel azonban mindkettő elektromosan pozitív, az elektromos töltés taszítása uralja a kölcsönhatást, legalábbis addig, amíg nagyon közel nem érnek. A normál anyagban is a pozitronok elektronokkal semmisülnek meg jóval azelőtt, hogy elérnék a protont. Ennek ellenére lenne mit keresni. Összességében jól látható, hogy a részecskék közötti taszító erők valóban a mechanikai erő részét képezik.

Az utolsó az elektronok közötti erős vonzóerő, amely egy másik erős Casimir-erő és az elektromágneses elmélet része.

Így már csak két erőnk marad. De mivel az elektronok és protonok elektromos töltéssel és mechanikai töltéssel rendelkeznek, nem lehet szétválasztani a két erőt. Matematikailag egyenértékűek a Maxwell-egyenletekkel, és a Maxwell-egyenletek egy változata mindkét erőt leírja. Mindkét erő hasonlóan viselkedik kvantumszinten is. Emiatt a két erő könnyen egyesül egyetlen elektromechanikus erővé, vagy ahogy máshol nevezem elektro-anyag erővé. 127

Az az állítás, hogy négy alapvető erő létezik, hazugság. A fizikusok régóta figyelmen kívül hagynak vagy tévednek számos erővel kapcsolatban, amelyeket kísérletileg igazoltak. Végső soron azonban minden erő egyetlen erő része.

126 John Archibald Wheeler, Annals of the New York Academy of Sciences, 480 (1986)

127 R. Fleming, „The Electro-Matter Force”,

https://www.researchgate.net/publication/284179658_The_Electro-Matter_Force

És most?

Az összes tantárgy közül egyedül a tudomány tartalmazza azt a leckét, hogy az előző generáció legnagyobb tanítóinak tévedhetetlenségébe vetett hit veszélye fenyeget. . . Tanuld meg a tudományból, hogy kételkedned kell a szakértőkben. Ami azt illeti, a tudományt másképpen is definiálhatom: a tudomány a szakértők tudatlanságába vetett hit. 128

Richard Feynman

Feynmannek biztosan igaza volt, de még ő sem gondolta volna, milyen rossz lett a modern fizika. És ez a lista nem tartalmaz sok más, jelenleg kritikai felülvizsgálat alatt álló elméletet. Ezenkívül minden általános fizika témakörben több tucat olyan altéma található, amelyeket érvénytelen tudományoknak lehet nevezni, és ezek közül csak néhányat érintettünk itt. A ma megjelenő fizikai tanulmányok túlnyomó többsége idő- és energiapazarlás, mivel az a sorsuk, hogy a történelem szemeteskukájába kerüljenek, sokak számára már a megjelenésük napján.

Fel kell ismernünk, hogy a fizika tudománya mögötti rendszer megbomlott. Természetellenes szakadék van az akadémiai közösség és a független kutatók között. Az akadémikusok olyan emberekkel veszik körül magukat, akik nem kérdőjelezik meg nyíltan tekintélyüket, noha a legtöbb egyetért Feynmannel abban, hogy ezt meg kell tenni. A függetlenek el vannak zárva attól, hogy folyóiratokban publikáljanak, épp úgy, hogy ne férhessenek hozzá a tudományos világban élő személyekhez komoly diskurzus céljából. A függetlenek a mainstream konferenciákon sem szerepelhetnek.

A folyóiratrendszer is megbomlott, a szerkesztők nem hajlandók figyelembe venni a mainstream nézetet megkérdőjelező ötleteket, még akkor sem, ha az ismert, hogy tévesek. A folyóiratok az információk megosztását is megakadályozzák azáltal, hogy korlátozzák a cikkekhez való hozzáférést. Azok az emberek, akiknek nincs a közelben nagy egyeteme, és nem engedhetik meg maguknak a magas díjakat, nem kaphatnak másolatokat. A cikkek és információk megosztásának nyílt platformon kellene történnie az egyszerű megosztás érdekében, nyitottabb tartalomengedélyezési rendszerrel. A szakértői értékelési rendszer amúgy is megbomlott; akár nyílt rendszer is lehetne a cenzúrával sújtott rendszer helyett.

Ami a következőt illeti, az első lépés az, hogy nyíltan felismerjük, hogy az éter valóban létezik, és dipólus jellegű. Ezután minden elméletet felül kell vizsgálni, hogy megbizonyosodjunk arról, hogy az összhangban van a vákuum-dipólusok létezésével. Ennek egy részét itt próbáltam megtenni, részletesebb információk pedig a The Zero-Point Universe című könyvemben találhatók.

Ezután szembe kell néznünk az alapvető megválaszolatlan kérdésekkel, mint például, hogy a testek hogyan mozognak az elektromágneses, mechanikai és gravitációs erők hatására. A testek nem varázslattal mozognak, létezik egy valódi fizikai mechanizmus, és ez a mechanizmus minden bizonnyal vákuum-ingadozásokkal jár.

Ezután meg kell értenünk a kvantumproblémákat, például a kvantumugrásokat, az alacsony energiájú magreakciókat, a fotonképződést, és azt, hogy a valószínűségi események hogyan hoznak egyedi eredményeket.

A fizikában nincs varázslat. Minél inkább ragaszkodunk a fizikai mechanizmusok megértéséhez mindannak, ami a legalapvetőbb szinteken történik, annál inkább korlátozzuk a problémákat. Sok esetben csak egyetlen megoldás marad. E megoldások közül néhányat ebben a könyvben is javasolunk.

És szabaduljunk meg a fizikában a tudományos-fantasztikus irodalomtól, vagy legalábbis tegyük annak kategóriájába. Ha a tudományos-fantasztikus irodalomról úgy beszélünk, mintha az a tudomány lenne a népszerű médiában, az megakadályozza, hogy a valódi fizikakutatást komolyan vegyük.

A sci-fi probléma is valami általánosabb dolog része. A fizikusok hajlamosak elméleteket bemutatni anélkül, hogy részletekbe mennének az elmélet hiányosságairól. Amint azt a 100 hazugság is mutatja, sok általános fizikaelméletben könnyű végzetes hibát találni, de ezekről a hibákról ritkán beszélnek nyíltan. A fizikusok utálják nyíltan beismerni, hogy a kedvenc elméleteik egy rakás szemét, de ez az első lépés a továbbhaladás felé.

Nem haladunk előre új dolgok, például nem létező részecskék, mezők és dimenziók kitalálásával sem, hogy megpróbáljuk kijavítani a hibákat vagy kitölteni a hiányosságokat egy elméletben. Úgy haladunk előre, hogy elmagyarázzuk, hogyan működnek a dolgok fizikailag, felhasználva azt, amiről tudjuk, hogy fizikailag valóságos.

És ne feledje, hagyja abba a számítást, és keresse meg a fizikai magyarázatot.

128 R. P. Feynman, The Pleasure of Finding Things p. 186-187, 1999

Téveszmék mint a nagy hazugságok

Hazugságok a 100 fejezetből:

Az éter felmelegíti az anyagtesteket 1

Az éter kinetikus energiaveszteséget okoz 1

Nincs éter nyugalmi keret 2

Maxwell éterhúzási hipotézise 2

A fény a forrás referenciakeretében halad 2

A fény sebessége az iránytól függ 2

A hullámok hullámokból állnak 3

A fotonok részecskék 4

Az elektromágneses mezők a fotonok sajátjai 4

A fotonok antirészecskék 5

Elektromágneses hatás távolról 8

Bármilyen ősrobbanás modell, amely mágneses monopólusokat igényel 10

Bármilyen anyagtermelési hipotézis, amely mágneses monopólusokat igényel 10

Bármilyen hipotézis, amely mágneses monopólusokat igényel 10

A fény sebessége a fény sajátossága 11

A relativisztikus keret-transzformációk szabványos referenciakeret nélkül is végrehajthatók 13

Feloldatlan paradoxonokat tartalmazó elméletek 13

A Michelson-Morley eredmény magyarázatához hosszúság kontrakcióra van szükség 14

Az üres tér órával rendelkezik 16

A proton tömege alapvető állandó 19

Az elektron tömege alapvető állandó 19

A neutron tömege alapvető állandó 19

Az univerzum összes energiája egy helyen sem hozna létre fekete lyukat 29

Az ősrobbanás modell megmagyarázza az anyagtermelést 32

Az időre vonatkozó nem végtelen kozmológiai modellek nem sértik az energia-megmaradás elvét 33

A nagy reccs 35

A fizika megmagyarázza a fotonképződést 37

A fizika megmagyarázza, hogy a tömeg hogyan okozza a gravitációt 52

Ponttöltés 53

Az elektronoknak nincs szerkezetük 53

A pályán vagy görbe úton haladó részecskéknek fotonokat kell sugározniuk 58

Minden kvark mezon modell 60

A fizikusok értik a béta-bomlás okát 64

A fizika megmagyarázza a gyenge kölcsönhatási energia-eloszlások okát A neutrínók okozzák a béta bomlási energia eloszlását 64

A W és Z részecskék elemiek 68

A mezonok közvetítik az erős erőt 69

Pauli kizárási elve felelős a nukleonok közötti taszításért 69

A protonok és neutronok közötti taszítás az erős erő része 69

Lepton megőrzés 72

Egy részecske nem elemi, ha van szerkezete 73

Proton bomlás 73

Relativisztikus tömeg 75

A Higgs mező 77

Multiverzumok 82

Görbült extra dimenziók 84

Szuperhúrok 85

M-elmélet 85

D-Branes 85

A részecskék húrként modellezhetők 85

Az idő egy fizikai dimenzió 86

Az elektromos állandó alapvető 87

A mágneses állandó alapvető 87

Warp meghajtók 88

Képzelt tömegmezők 89

Szuperszimmetria 85

G állandó 91

A Chandrasekhar határ 93

Dyson hipotézise az anyag szilárdságáról 93

Degenerált anyag. 93

Elektron-degeneráció 93

Elektron degenerált anyag 93

Proton degeneráció 93

Neutron degeneráció 93

Neutron degenerált anyag 93

Kvark degenerált anyag 93

Elvetemült téridő 95

A nagy neutroncsillagok összeomlanak 95

Egy elmélet tartalmazhat szingularitásokat 97

Fehér lyukak 98

Az anyag előállítható a nem térből 99

A nullponti energia nem energia 99

A nullponti energia negatív energia 99

Negatív Energia 99

Nullaponti energiából nem lehet anyagot előállítani 99

A gyenge erő alapvető erő 100

Az erős erő alapvető erő 100

Vége